Monte Carlo tree search 学习
https://en.wikipedia.org/wiki/Monte_Carlo_tree_search
http://mcts.ai/about/index.html
UCT算法(Upper Confidence Bound Apply to Tree),即信任度上限树,是一种博弈树搜索算法,该算法将蒙特卡洛树搜索(Monte—Carlo Tree Search,MCTS)方法与UCB公式结合,在超大规模博弈树的搜索过程中相对于传统的搜索算法有着时间和空间方面的优势。
UCB1(Upper Confidence Bound) 公式
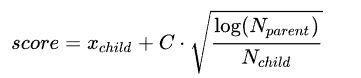
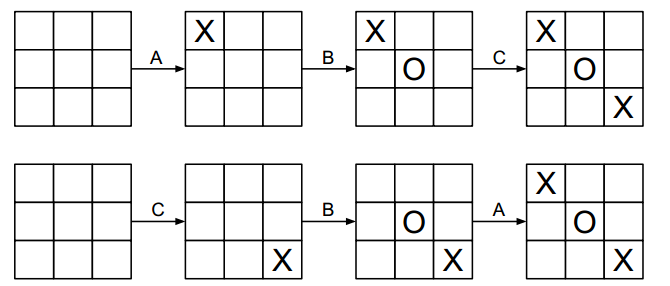
AMAF(All Moves As First) 它视使棋盘达到某一相同状态的着法都等价的,不论由谁在何时完成
RAVE(Rapid Action Value Estimation) 快速动作值估计
Monte Carlo tree search 学习的更多相关文章
- Introduction to Monte Carlo Tree Search (蒙特卡罗搜索树简介)
Introduction to Monte Carlo Tree Search (蒙特卡罗搜索树简介) 部分翻译自“Monte Carlo Tree Search and Its Applicati ...
- 蒙特卡罗方法、蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)初探
1. 蒙特卡罗方法(Monte Carlo method) 0x1:从布丰投针实验说起 - 只要实验次数够多,我就能直到上帝的意图 18世纪,布丰提出以下问题:设我们有一个以平行且等距木纹铺成的地板( ...
- Programming a Hearthstone agent using Monte Carlo Tree Search(chapter one)
Markus Heikki AnderssonHåkon HelgesenHesselberg Master of Science in Computer Science Submission dat ...
- Monte Calro Tree Search (MCTS)
https://blog.csdn.net/natsu1211/article/details/50986810, 感谢分享! Intro最近阿法狗和李师师的人机大战着实火了一把,还顺带捧红了柯杰,古 ...
- 论文笔记:Mastering the game of Go with deep neural networks and tree search
Mastering the game of Go with deep neural networks and tree search Nature 2015 这是本人论文笔记系列第二篇 Nature ...
- 增强学习(四) ----- 蒙特卡罗方法(Monte Carlo Methods)
1. 蒙特卡罗方法的基本思想 蒙特卡罗方法又叫统计模拟方法,它使用随机数(或伪随机数)来解决计算的问题,是一类重要的数值计算方法.该方法的名字来源于世界著名的赌城蒙特卡罗,而蒙特卡罗方法正是以概率为基 ...
- 强化学习读书笔记 - 05 - 蒙特卡洛方法(Monte Carlo Methods)
强化学习读书笔记 - 05 - 蒙特卡洛方法(Monte Carlo Methods) 学习笔记: Reinforcement Learning: An Introduction, Richard S ...
- [matlab]Monte Carlo模拟学习笔记
理论基础:大数定理,当频数足够多时,频率可以逼近概率,从而依靠概率与$\pi$的关系,求出$\pi$ 所以,rand在Monte Carlo中是必不可少的,必须保证测试数据的随机性. 用蒙特卡洛方法进 ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
随机推荐
- loadrunner json参数化
因为json格式有{},所以LR参数化时如果也用默认的{}的话,会冲突,这样脚本运行时就无法识别,导致不能正确的读取参数化文件里的内容,此时把参数化的{}改成其他符号即可,比如<>
- 1080 MOOC期终成绩
对于在中国大学MOOC(http://www.icourse163.org/ )学习“数据结构”课程的学生,想要获得一张合格证书,必须首先获得不少于200分的在线编程作业分,然后总评获得不少于60分( ...
- 阶段01Java基础day10面向对象05
10.01_面向对象(package关键字的概述及作用) A:为什么要有包 将字节码(.class)进行分类存放 B:包的概述 C:包的作用 10.02_面向对象(包的定义及注意事项) A:定义包的格 ...
- spring 配置 applicationContext.xml
<?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.spr ...
- JAVA基本类型和包装类
JAVA的包装类 Java语言是一个面向对象的语言,但是Java中的基本数据类型却是不面向对象的,这在实际使用时存在很多的不便,为了解决这个不足,在设计类时为每个基本数据类型设计了一个对应的类进行代表 ...
- Final阶段第1周/共1周 Scrum立会报告+燃尽图 05
作业要求[https://edu.cnblogs.com/campus/nenu/2018fall/homework/2484] 版本控制:https://git.coding.net/liuyy08 ...
- 20165214 实验二 Java面向对象程序设计
一.实验报告封面 课程:Java程序设计 班级:1652班 姓名:朱文远 学号:20165214 指导教师:娄嘉鹏 实验日期:2018年4月16日 实验时间:13:45 - 15:25 实验序号:二 ...
- day 32 子进程的开启 及其用法
开启两种子进程的两种方式# # # 1 传统方式# from multiprocessing import Process# import time# def task(name):# print ( ...
- vue项目功能
vue-router { path: '/', name: 'home', // 路由的重定向 ...
- 联想 Lenovo PWR-G60 无线掌中宝拆机
从朋友那里弄了台Lenovo PWR-G60,现在已经停产了,淘宝上某店卖的国产WIFI Pineapple貌似就是拿这个刷的,打算出篇DIY教程 现在人在外地,编程器.热风枪.烙铁工具啥的都没有,更 ...
