Frobenius norm(Frobenius 范数)
Frobenius 范数,简称F-范数,是一种矩阵范数,记为||·||F。
矩阵A的Frobenius范数定义为矩阵A各项元素的绝对值平方的总和,即
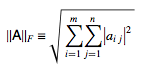
- 可用于 利用低秩矩阵来近似单一数据矩阵。
- 用数学表示就是去找一个秩为k的矩阵B,使得矩阵B与原始数据矩阵A的差的F范数尽可能地小。
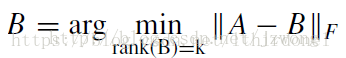
Frobenius norm(Frobenius 范数)的更多相关文章
- 弗罗贝尼乌斯範数(Frobenius norm)
弗罗贝尼乌斯範数 对 p = 2,这称为弗罗贝尼乌斯範数(Frobenius norm)或希尔伯特-施密特範数( Hilbert–Schmidt norm),不过后面这个术语通常只用于希尔伯特空间.这 ...
- numpy.linalg.norm(求范数)
1.linalg=linear(线性)+algebra(代数),norm则表示范数. 2.函数参数 x_norm=np.linalg.norm(x, ord=None, axis=None, keep ...
- python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)(向量的第二范数为传统意义上的向量长度),(如何求取向量的单位向量)
求取向量二范数,并求取单位向量(行向量计算) import numpy as np x=np.array([[0, 3, 4], [2, 6, 4]]) y=np.linalg.norm(x, axi ...
- Frobenius Norm
http://mathworld.wolfram.com/FrobeniusNorm.html
- 【Matlab开发】matlab中norm范数以及向量点积、绘图设置相关
[Matlab开发]matlab中norm范数以及向量点积.绘图设置相关 标签(空格分隔): [Matlab开发] 声明:引用请注明出处http://blog.csdn.net/lg125915677 ...
- Frobenius inner product
https://en.wikipedia.org/wiki/Frobenius_inner_product Frobenius norm
- numpy中np.linalg.norm()求向量、矩阵的范数
np.linalg.norm() # linalg = linear(线性) + algebra(代数), norm表示范数 x_norm = np.linalg.norm(x, ord=None ...
- norm函数的作用,matlab
格式:n=norm(A,p)功能:norm函数可计算几种不同类型的返回A中最大一列和,即max(sum(abs(A))) 2 返回A的最大奇异值,和n=norm(A)用法一样 inf 返回A中最大一行 ...
- paper 126:[转载] 机器学习中的范数规则化之(一)L0、L1与L2范数
机器学习中的范数规则化之(一)L0.L1与L2范数 zouxy09@qq.com http://blog.csdn.net/zouxy09 今天我们聊聊机器学习中出现的非常频繁的问题:过拟合与规则化. ...
随机推荐
- [Python] networkx入门 转
networkx是python的一个第三方包,可以方便地调用各种图算法的计算. 通过调用python画图包matplotlib能实现图的可视化. 1.安装 正好整理一下python第三方包的安装方法. ...
- ubuntu16.04下idea、webstorm等开发工具不能输入中文问题
问题: ubuntu16.04下idea.webstorm开发工具不能输入中文,就算切换到中文输入法输入的也是英文字母. 解决方案: 1.vim打开开发工具的启动文件(idea下就是idea.sh) ...
- MySQL常用内置变量
MySQL用很多常用的内置变量,掌握这些内置变量后对于我们快速获取当前MySQL的配置有很大帮助,下面就来列举几个常用的变量. 查看当前MySQL版本号信息.show variables like ...
- what does GIT PUSH do exactly?
有效理解 git 的对象模型 https://stackoverflow.com/questions/26005031/what-does-git-push-do-exactly 所谓分支, 就是一个 ...
- HttpRunner框架(一)
HttpRunner 是一款面向 HTTP(S) 协议的通用测试框架,只需编写维护一份 YAML/JSON 脚本,即可实现自动化测试.性能测试.线上监控.持续集成等多种测试需求. 中文使用文档地址:h ...
- webpack通过postcss-loader添加浏览器前缀
在webpack中,我们可以很方便的使用autoprefixer来为css3属性添加不同的浏览器前缀. 首先,需要安装autoprefixer不用多说了,其次是安装postcss-loader(npm ...
- vue安装及axios、stylus、iview的安装流程整理
现在做的项目中主要用到以下几个安装包,所以整理下流程: 使用命令行工具npm新创建一个vue项目 vue中axios的安装和使用 在vue项目中stylus的安装及使用 如何在vue中全局引入styl ...
- spring boot集成 servlet自动注册的两种方式
有两种方式:(两种方式同时存在时,@Bean优先@ServletComponentScan实例化,生成两个对象) 1)通过@ServletComponentScan类注解 扫描 带有@WebServl ...
- jenkins配置邮件 -- com.sun.mail.smtp.SMTPSenderFailedException: 550 5.7.1 Client does not have permissions to send as this sender
jenkins配置邮件设置 发送邮件测试时,报错: com.sun.mail.smtp.SMTPSenderFailedException: Client does not have permissi ...
- Ubuntu16.04安装Anaconda (转)
一. Anaconda下载 Anaconda 官方下载链接: https://www.continuum.io/downloads 根据自己的系统选择下载32位还是64位. 二. 进入下载目录 如 ...
