【OS】Heap & Stack

操作系统概念的堆、栈不同于数据结构的堆、栈。

C 语言中，一切指针占 4 字节，这意味着指针指向 RAM 中的地址可以有 2³² 个，最小的地址是 0，最大的地址是 2³¹ - 1。

（一）堆：

堆空间在内存中是一个字节的沙盒。

malloc()、free()、realloc() 是程序员使用软件，通过特定的启发式策略管理内存的。malloc() 不仅返回一块内存的基地址，它还留出额外的头部空间记录了分配出去的内存块的实际大小。

经过一些分配释放后，堆中的内存碎片化了，形成有大有小的空闲块。因此使用一个内存块的链表（存储下个空闲内存块的地址）来记录空闲的内存块，这个链表称为空闲表，方便 malloc() 等函数继续管理内存。

（二）栈：

当进行函数调用时，函数调用会强制地为局部变量申请空间，这些局部变量的内存就在 RAM 中被称为“栈”（stack segment）的子集中。

调用 main() 函数时会得到它的局部变量，它们 alive & active，当 main() 调用一个子函数时，main() 的变量就暂时被屏蔽掉了，无法访问；当继续调用子函数的子函数时，这一系列变量都被分配好空间，但只有在最底部的函数中的局部变量才是 alive 的，并可以通过变量名访问。

每当函数调用时，系统都会为其创建活动记录。

如调用以下 void fun(int para1, int para2) 函数，

void fun(int para1, int *para2) {
    char a[];
    short *b;
    // 以下略
    ...
}

系统会形成这样的布局。

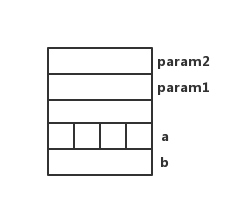
注意：

（1）函数形参从左到右，分别存放在内存的低地址到高地址，通俗地讲，第二个参数在第一个参数之上。

（2）位于函数形参和局部变量中间的部分，存储着调用函数的某些信息，告诉我们“哪块代码”调用了 fun()，这里称为 saved PC。

另一个递归调用阶乘函数的例子：

int fact(int n) {
    if (n == )    return ;
    return n * fact(n - );
}

我们用模拟汇编指令的方法写该 <fact> 函数：

 R1 = M[SP + ];    // 将 n 的值存放到寄存器 R1 中
 BNE R1, , PC + ;    // Branch分支指令，R1 和 0 Not Equal 时，跳转
 RV = ;
 RET;    // RV 存放返回值 1，调用 RET 返回
 R1 = M[SP + ];
 R1 = R1 - ;    // R1 = n - 1
 SP = SP - ;
 M[SP] = R1;
 CALL <fact>;    // 继续调用 <fact>，此时RV已经存放了 <fact> 返回的有意义的值
 SP = SP + ;
 R1 = M[SP + ];
 RV = RV * R1;
 RET;

其中，

SP（Stack Pointer）是一个特殊的寄存器，指向当前的相关活动记录的基地址，即当前栈的最低地址。

RV 存放返回值，调用 RET 时讲其返回给函数调用者。

本例假设系统中每一条指令都是 4 字节宽，因此第 2 行指令是 PC，则满足条件跳转到的 PC + 12 则是第 5 行。

首先，假设某函数，可能是 fact(4) 或其他函数，调用了 fact(3)。

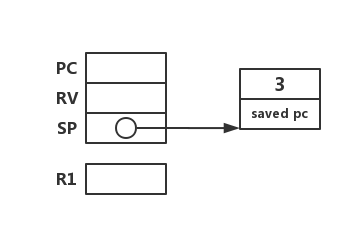
如上个例子所示，函数调用时，为形参 3 创建的内存空间构成了当前活动记录的上半部分；SP 指向栈的最低地址，该处的 saved PC 保存了那个“某函数”的调用信息（哪行代码调用了 fact(3)）。

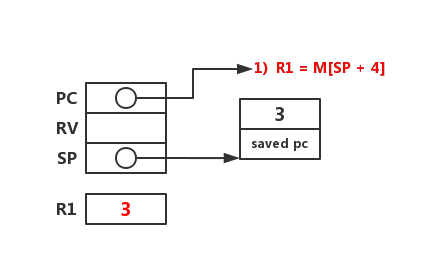
将 n 的值 3 存放到寄存器 R1 中。

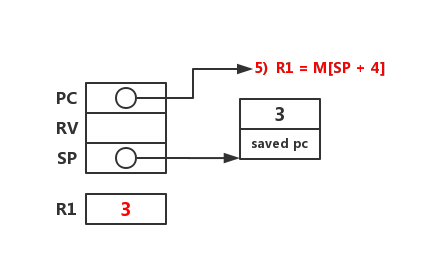
n(3) ！= 0，跳转到第 5 行。

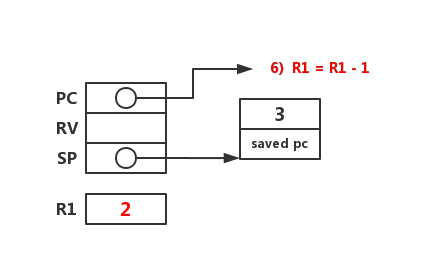
准备 n - 1 的值 2。

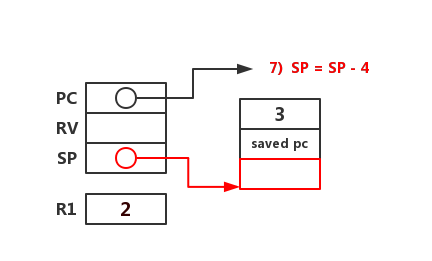
创建下个要调用的函数 fact(2) 的活动记录的上半部分。

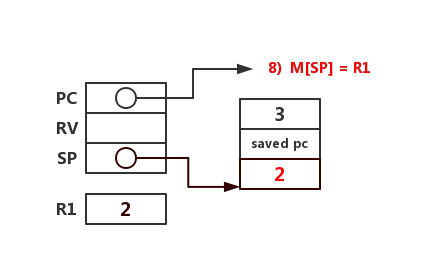
将 2 写入当前栈帧（stack frame）中。

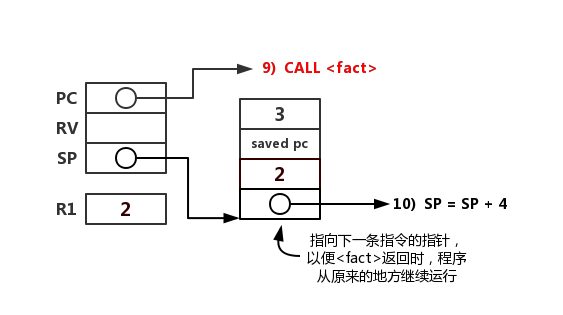
调用 fact(2)，函数 fact(2) 活动记录的 saved PC 保存了 fact(3) 函数指令第 10 行的地址。

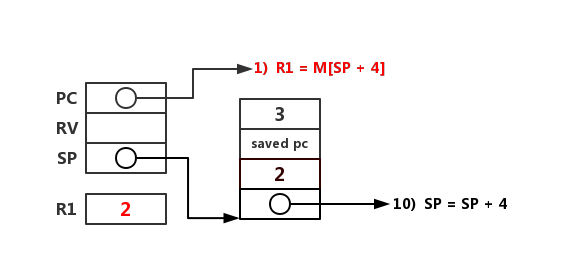
进入 fact(2)，当前 PC 执行到 fact(2) 的第 1 条指令：将 n 的值 2 保存到寄存器 R1 中。

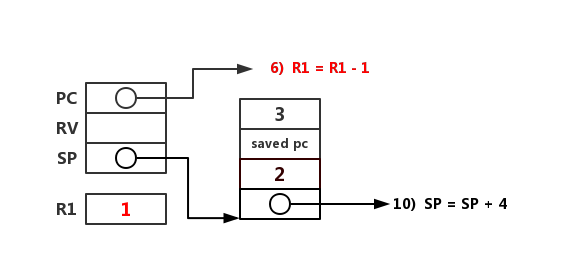
同上，继续执行 fact(2)，开始准备 n - 1 的值 1。

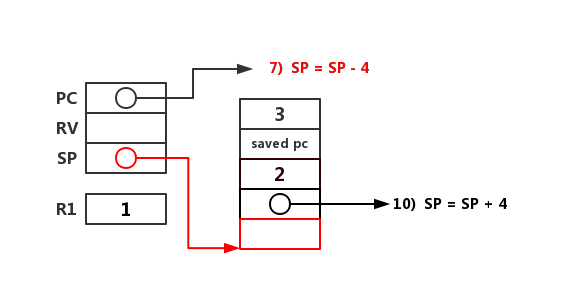
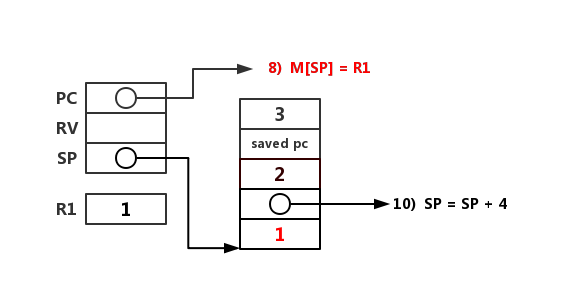
同上，创建 fact(1) 的活动记录的上半部分。

……

直到调用 fact(0)。

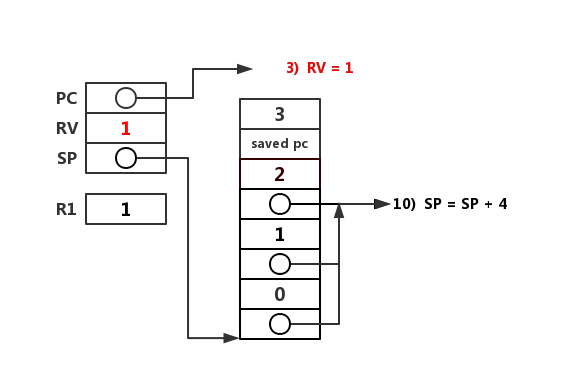
函数 fact(0) 返回值为 1。

开始层层返回。

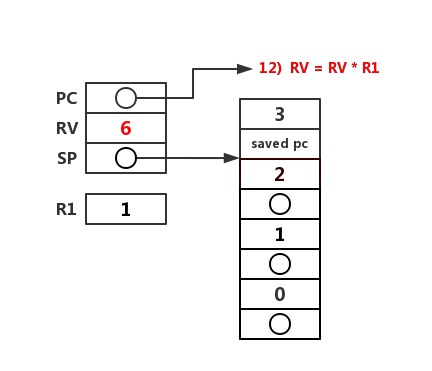
最后返回值为 6，注意此时 SP 指向的是当前活动记录的基地址。

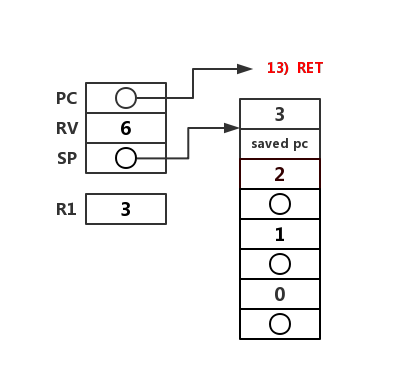
最终将 6 返回给调用这个原始调用 fact(3) 的函数。

到此，fact(3) 执行完毕。

以上