剑指Offer 10. 矩形覆盖 （递归）

题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

题目地址

https://www.nowcoder.com/practice/72a5a919508a4251859fb2cfb987a0e6?tpId=13&tqId=11163&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

思路

以2x8的矩形为例。示意图如下：

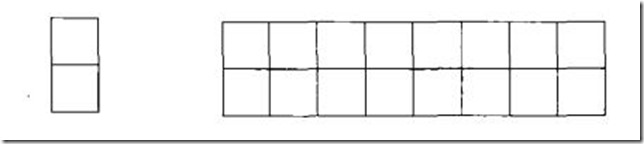
我们先把2x8的覆盖方法记为f(8)。用第一个1x2小矩阵覆盖大矩形的最左边时有两个选择，竖着放或者横着放。当竖着放的时候，右边还剩下2x7的区域，这种情况下的覆盖方法记为f(7)。接下来考虑横着放的情况。当1x2的小矩形横着放在左上角的时候，左下角和横着放一个1x2的小矩形，而在右边还剩下2x6的区域，这种情况下的覆盖方法记为f(6)。因此f(8)=f(7)+f(6)。此时我们可以看出，这仍然是斐波那契数列。

Python

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        if number <= 3:
            return number
        a, b = 1, 2
        for i in range(2,number):
            c = a+b
            a,b = b,c
        return c
 
if __name__ == '__main__':
    result = Solution().rectCover(4)
    print(result)