洛谷 P3237 [HNOI2014]米特运输

题面链接

get到新技能当然要来记录一下辣

题意：给一棵树，每个点有一个权值，要求同一个父亲的儿子的权值全部相同，父亲的取值必须是所有儿子的权值和，求最少的修改数量

sol：自己瞎鸡巴yy一下可以发现，如果根节点（当做1来算）权值确定，整棵树所有点的权值也都确定了，再一想，其实只要有一个点的权值确定，那么根节点的权值也必然确定了 配个图吧qaq(没事找事)

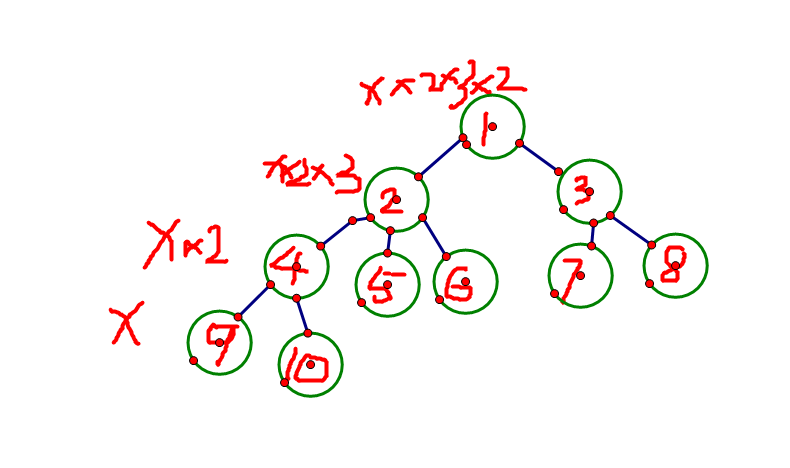
于是发现对于每个点的权值，求出其对应的根节点的权值，找到出现次数最多的，就可以知道答案了啊

但是全部乘起来显然会爆蛋，看了fks大佬的blog知道了还可以用log，因为log(a*b)=log(a)+log(b)，技能get,实现不是很难。

#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N=;const double eps=1e-;
int n;
double v[N],f[N];
vector<int>G[N];
inline void dfs(int x,double sum)
{
    int i; f[x]=(double)sum+log(v[x]);
    for(i=;i<G[x].size();i++)
    {
        dfs(G[x][i],sum+(double)log(G[x].size()));
    }
}
int main()
{
    int i,x,y,re=,tmp=; scanf("%d",&n); for(i=;i<=n;i++)scanf("%lf",&v[i]);
    for(i=;i<n;i++)
    {
        scanf("%d%d",&x,&y); G[x].push_back(y);
    }dfs(,(double)(1.00)); sort(f+,f+n+);
    for(i=;i<=n;i++)
    {
        if(f[i]-f[i-]<eps)tmp++,re=max(re,tmp);else tmp=;
    }printf("%d\n",n-re);
}