【OpenGL ES】透视变换原理

1 前言

​ MVP矩阵变换 中主要介绍了模型变换（平移、旋转、对称、缩放）和观测变换基本原理，本文将介绍透视变换的基本原理。

​ 如下图，近平面和远平面间棱台称为视锥体，表示可见区域范围，视锥体以外的空间将被裁剪丢弃，视锥体内的模型通过透视变换投影到近平面上，近平面上得到的平面图形就是屏幕上要显示的模型的图形。

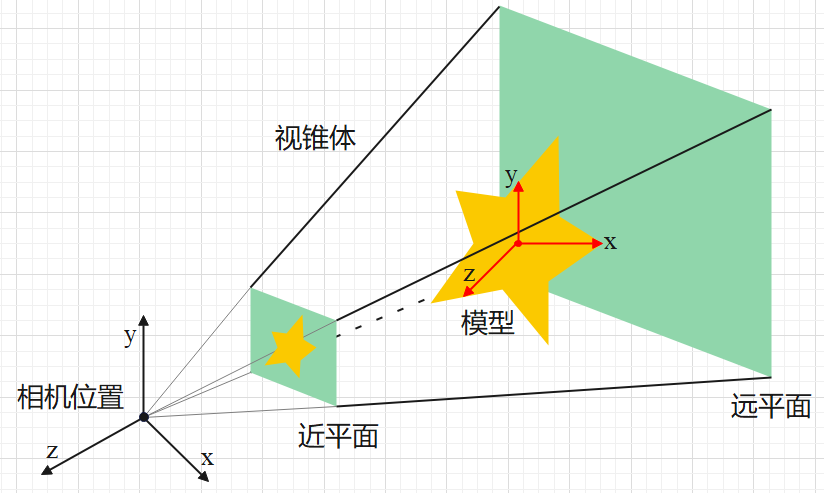
​ 近平面的高度为 2（区间为 [-1, 1]，为方便计算，已归一化），宽度也为 2。当相机位置和模型位置已固定时，由于近平面的宽高已固定，因此可以通过平移近平面的位置控制模型显示的缩放大小。

2 透视变换原理

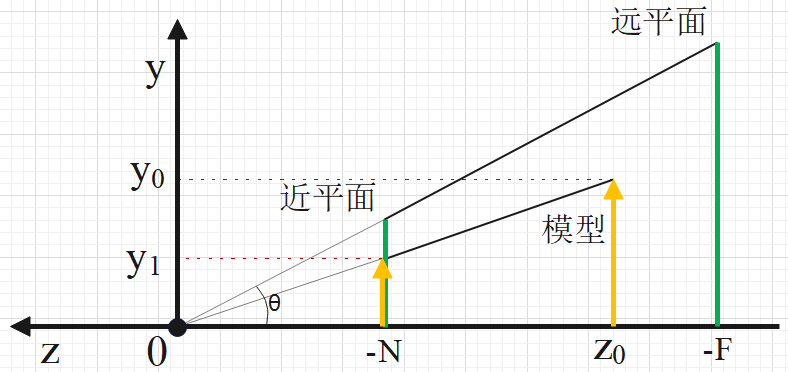
​ 如下图，在视图坐标系下，已知近平面和远平面距离原点的距离分别为 N 和 F，近平面高度和宽度都为 2，假设视锥体内任意一点的坐标为 (x0, y0, z0)，经透视投影后的坐标为 (x1, y1, z1)。

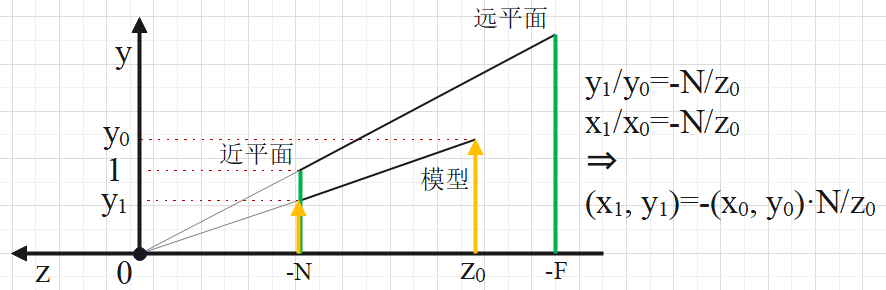
​ 由于近平面的宽高都是 2，即宽高比为 1: 1，但是 ViewPort 一般不是 1: 1，为了避免投影成像变形，通常将投影后的 x 坐标除以 ViewPort 的宽高比（假设为 r），因此有如下公式：

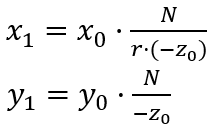
​ 由于 z0 是个变量，导致 (x1, y1) 与 (x0, y0) 之间不是线性关系。为了方便使用线性变换描述透视投影，将透视投影分为 2 个步骤：透视变换、透视分割。

​ 1）透视变换

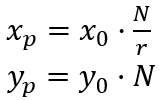
​ 2）透视分割

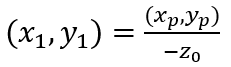
​ 其中，x0, y0 是模型坐标，xp, yp 是透视变换后的坐标，x1, y1 是透视投影（或透视分割）后的坐标。

​ 透视投影划分 2 步后，透视变换可以使用如下方式表示：

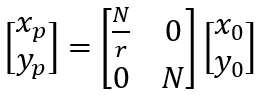
​ 经透视投影后，x 轴和 y 轴的坐标都被归一化到 [-1, 1] 区间内，z 轴坐标同样也需要归一化到 [-1, 1] 区间内。本来z1 与 z0 之间应该是线性关系，但是考虑到 (xp, yp, zp) 与 (x0, y0, z0) 之间需要使用矩阵表示，即 zp 与 z0 之间存在线性关系，因此，有如下函数关系：

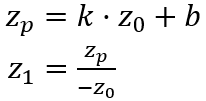
​ 进一步得到 z1 与 z0 的函数关系如下：

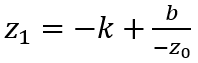
​ 使用待定系数法将 (-N, -1), (-F, 1) 代入求得 k 和 b 的值如下：

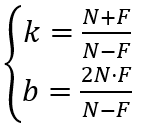
​ 因此，zp 与 z0 之间的函数关系如下：

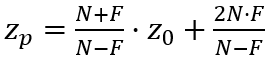
​ 经透视变换后，接着需要进行透视分割，即将 (xp, yp, zp) 除以 (-z0)，为保证透视变换后 z0 的信息不被丢失，将 -z0 值保存到第四维空间（即 w 维）中。因此，透视变换可以进一步使用如下方式表示：

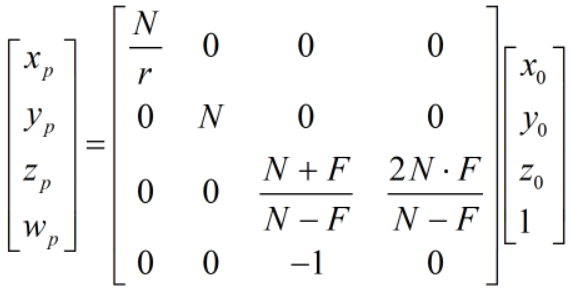
​ frustumM 方法源码如下，m 是透视变换返回的矩阵；offset 为索引偏移，表示 m 中 offset 之前的数不参与变换，通常取 0；(left, right, bottom, top) 为投影平面的边框，通常取 (-ratio, ratio, -1, 1)（ratio为 ViewPort 宽高比）；near 为近平面到相机的距离；far 为远平面到相机的距离。

public static void frustumM(float[] m, int offset,
		float left, float right, float bottom, float top,
		float near, float far) {
    ... //输入合法性校验
	final float r_width  = 1.0f / (right - left);
	final float r_height = 1.0f / (top - bottom);
	final float r_depth  = 1.0f / (near - far);
	final float x = 2.0f * (near * r_width);
	final float y = 2.0f * (near * r_height);
	final float A = (right + left) * r_width;
	final float B = (top + bottom) * r_height;
	final float C = (far + near) * r_depth;
	final float D = 2.0f * (far * near * r_depth);
	m[offset + 0] = x;
	m[offset + 5] = y;
	m[offset + 8] = A;
	m[offset +  9] = B;
	m[offset + 10] = C;
	m[offset + 14] = D;
	m[offset + 11] = -1.0f;
	m[offset +  1] = 0.0f;
	m[offset +  2] = 0.0f;
	m[offset +  3] = 0.0f;
	m[offset +  4] = 0.0f;
	m[offset +  6] = 0.0f;
	m[offset +  7] = 0.0f;
	m[offset + 12] = 0.0f;
	m[offset + 13] = 0.0f;
	m[offset + 15] = 0.0f;
}

​ 透视变换除了 frustumM 方法，还可以使用 perspectiveM 方法，公式如下：

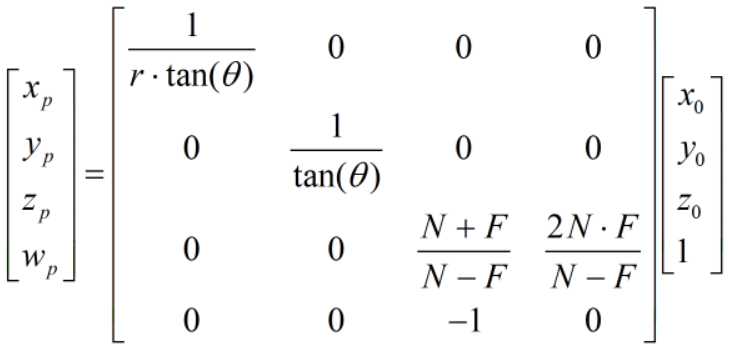
​ 其中，r 为 ViewPort 宽高比，θ 为视野角的一半。与 frustumM 方法相比，perspectiveM 方法仅对 z 进行了归一化，未对 x, y 进行归一化。

​ perspectiveM 方法源码如下，m 是透视变换返回的矩阵；offset 为索引偏移，表示 m 中 offset 之前的数不参与变换，通常取 0；fovy 为视野角度（角度制）；aspect 为 ViewPort 宽高比；zNear 为近平面到相机的距离；zFar 为远平面到相机的距离。

public static void perspectiveM(float[] m, int offset,
	  float fovy, float aspect, float zNear, float zFar) {
	float f = 1.0f / (float) Math.tan(fovy * (Math.PI / 360.0));
	float rangeReciprocal = 1.0f / (zNear - zFar);

	m[offset + 0] = f / aspect;
	m[offset + 1] = 0.0f;
	m[offset + 2] = 0.0f;
	m[offset + 3] = 0.0f;

	m[offset + 4] = 0.0f;
	m[offset + 5] = f;
	m[offset + 6] = 0.0f;
	m[offset + 7] = 0.0f;

	m[offset + 8] = 0.0f;
	m[offset + 9] = 0.0f;
	m[offset + 10] = (zFar + zNear) * rangeReciprocal;
	m[offset + 11] = -1.0f;

	m[offset + 12] = 0.0f;
	m[offset + 13] = 0.0f;
	m[offset + 14] = 2.0f * zFar * zNear * rangeReciprocal;
	m[offset + 15] = 0.0f;
}

​ 声明：本文转自【OpenGL ES】透视变换原理