Codeforces Round 941 (Div. 2) cf 941 div2 A~D

每题都有AC代码在伸缩代码框请留意！！

A. Card Exchange

-------------------------------------------题解----------------------------------

选择任意K张相同的牌替换成k-1张任意的牌，也就是说只要有一组牌相同的数量大于k就可以获得最大k-1相同的其他牌，按照这个策略便可以替换掉所有牌最后只剩下k-1张牌。，如果没有牌相同的数量大于等于k那就无法完成第一次替换，也没有后面的替换了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a[105];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,k;
        cin>>n>>k;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
        }
        map<int,int>m;
        int jud=0;
        for(int i=1;i<=n;i++)
        {
            m[a[i]]++;
            if(m[a[i]]>=k) jud=1;
        }
        if(jud==1) cout<<k-1<<endl;
        else cout<<n<<endl;
    }
}

B. Rectangle Filling

-------------------------------------题解-----------------------------------

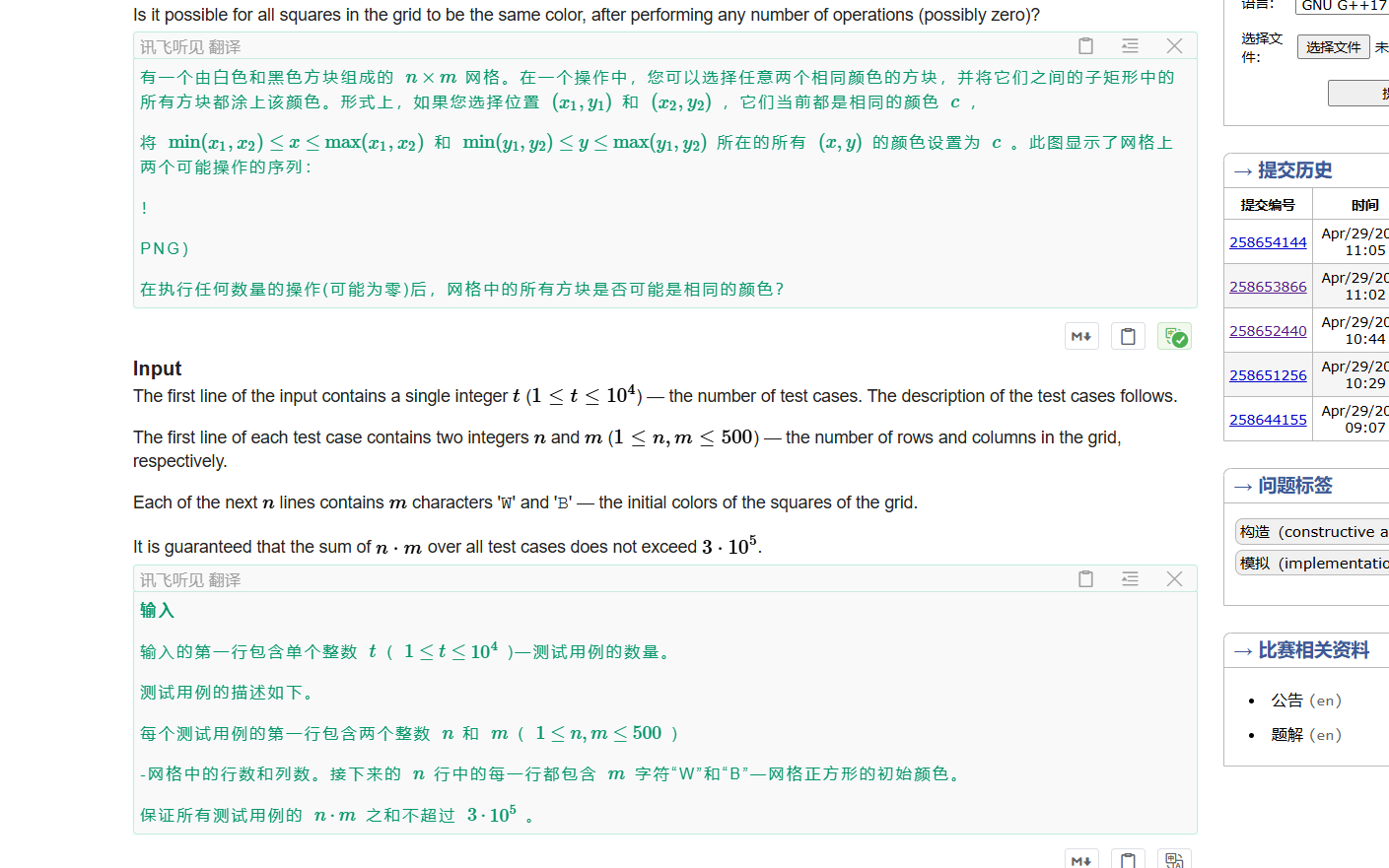
题意为选定一个矩形的左上角右下角，或者选定一个矩形的右上角和左下角，将这个矩形变为一个颜色，论能否把这个n*m的大矩形全变成一个颜色。

首先判断是不是本来就是纯色如果是直接跳出不是再进行下面的判断，然后先判断最边上的四条线是否是纯色，如果是纯色的话这个题就无法把他们变成纯色(原图不是纯色的情况下)反之则可以，然后特判一下只有单行或者只有单列的情况，有点复杂不过我看其他人的题解好像都不简单

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
char a[505][505];
ll b[2*N];
const int mod=998244353;
vector<ll> v;
int main()
{  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    ll t;
    cin>>t;
    while(t--)
    {
    	ll n,m;
    	cin>>n>>m;
    	int num=0;
    	for(ll i=1;i<=n;i++)
    	{
    		for(ll j=1;j<=m;j++)
    		{
    			cin>>a[i][j];
    			if(a[i][j]=='W') num++;
			}
		}
		int jud=0;
		int num1=0,num2=0;
		for(int i=1;i<=n;i++)
		{
			if(a[i][1]=='W') num1++;
			if(a[i][m]=='W') num2++;

		}
		if((num1==0&&num2==n)||(num1==n&&num2==0)) jud=1;
		num1=0,num2=0;
		for(int i=1;i<=m;i++)
		{
			if(a[1][i]=='W') num2++;
			if(a[n][i]=='W') num1++;
		}
		//cout<<num1<<" "<<num2<<endl;
		if((num2==0&&num1==m)||(num2==m&&num1==0)) jud=1;

		//cout<<jud<<endl;
		if(n==1)
		{
			if(a[1][1]!=a[1][m]) jud=1;
			else jud=0;
		}
		if(m==1)
		{
			if(a[n][1]!=a[1][1]) jud=1;
			else jud=0;
		}
		if(a[1][1]==a[n][m]) jud=0;
		if(a[1][m]==a[n][1]) jud=0;
		if(num==n*m||num==0) jud=0;
	//	cout<<num<<endl;

		if(jud!=1) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;

	}
	return 0;
}

C. Everything Nim

-------------------------------------------------题解-----------------------------------------

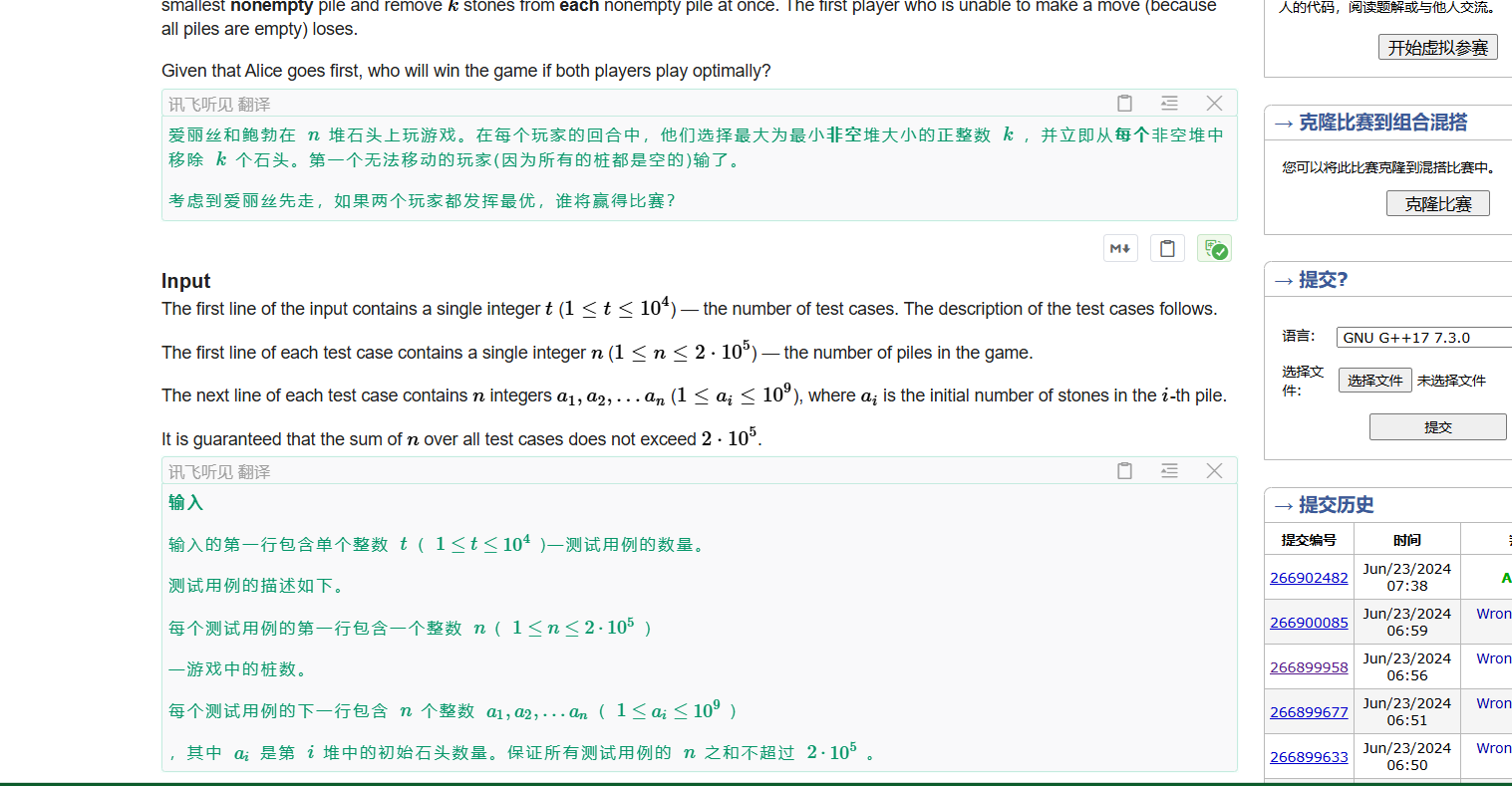
alice bob 双方有一段时间会被硬控，比如你把给你的数组sort以后 如果出现1 2 3 4 5这样的序列那A每次只能拿一个B也是相同直到双方拿完这一段1 2 3 4 5的序列，已知这个以后，我

们来说一下这个题取胜的策略，比如现在有2 3 5 7 9 A可以控制，让B 每次拿走一堆中的最后一个 比如在这个序列中A拿2 第一堆被拿完第二堆剩一个 B是不是只能拿完第二堆依照这个策

略直到剩最后一堆的时候A依然是先手，他这时候就可以一次拿完最后一堆让A赢得游戏。但是如果是B先手他是不是可以采取相同的策略？答案当然是可以的，那么我们如何判断谁是真正的先

手？就和我们上文中说的“硬控”有关了 所以我们要判断双方被硬控完之后谁是先手，谁便会按照最优策略赢得游戏 ，这里边需要对一整个序列取从1开始的mex 函数| (不懂mex函数的我来解释一下)

mex(1 6 5 3)=2就会出现 2 mex（1 1 4 5 1 4）也是2 mex（2 5 6） =1就是 mex函数取得是从1到n这个顺序中第一个没在序列里出现的数就叫 mex函数。

回到正题，我们只需要整个数组的mex函数（手写）是 奇数还是偶数就好奇数就是结束后A先手，反之则是B先手。完成这个之后需要特判一下， 如果双方被"硬控"完之后数列直接结束了

比如n=5，数组为1 2 3 4 5 那么数列结束之后先手的一方输了，特判完这种情况就可以按照上述的策略判断谁赢了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
typedef long long ll;
ll a[N];
int main()
{
    int t;
    cin>>t;
    for(int i1=1;i1<=t;i1++)
    {
        ll n;
        cin>>n;
        for(ll i=1;i<=n;i++) cin>>a[i];
        sort(a+1,a+1+n);
        ll q=1;
       ll w=0;
        for(ll i=1;i<=n;i++)
        {
            if(a[i]!=a[i-1]&&a[i]==q) q++;
              if(a[i]!=a[i-1])w++;
        }

        if((q%2==1&&q-1!=w)||(q%2==0&&q-1==w)) cout<<"Alice"<<endl;

        else cout<<"Bob"<<endl;
    }
}

D D. Missing Subsequence Sum

有难度的构造，能看到这里的都是糕手了，说的尽量简化一些

-----------------------------------题解------------------------------

我么首先把一整个n分成两部分来看 k-1部分（下统称k1）,k+1（下统称k2)

k1部分很简单，我们只需要用二进制的思想用 1 2 4 8..2的n次方<=k-1就行 然后最后再补上一个 k-1-2的n次方这样就能全部凑出,然后我通过k==1时候的方法，总结出了以下思路

，按照该方法构造就可以

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll a[N];
int main()
{
    int t;
    cin>>t;
    ll o=0;
    while(t--)
    {  o++;
        int n,k;
        cin>>n>>k;
       // if(o==136) cout<<n<<endl;
        ll cnt=0;
        ll sum=0;
       if(k==1)
       {
       ll jud=0;
    	sum=1;
    	cnt=0;
    	a[1]=2;
    	ll p=1;
    	ll q=2;
    	while(sum<n)
    	{
    		 p++;
           if(sum<k-1)
           {
           	  if(k-1-sum>=pow(2,cnt+1)) cnt++,a[p]=pow(2,cnt),sum+=pow(2,cnt);
           	  else
           	  {
           	  	a[p]=k-1-sum;
           	  	sum=k-1;
			  }
		   }
		   else
		   {
				if(jud==0)
				{
					jud=1;
					a[p]=k+1;
					sum+=k+1;
					p++;
					a[p]=3*k+1;
					p++;
					a[p]=2*k+1;
				//	sum+=3*k+1+2*k+1;
				}
				else
				{
					a[p]=pow(2,q)*k+1;
					sum+=pow(2,q)*k+1;
					q++;
				}
			//	cout<<1<<endl;

		   }

		}
			cout<<p<<'\n';
		   for(ll i=1;i<=p;i++)cout<<a[i]<<" ";
		   cout<<'\n';
       }

    else
    {   ll jud=0;
    	sum=1;
    	cnt=0;
    	a[1]=1;
    	ll p=1;
    	ll q=2;
    	while(sum<n)
    	{
    		 p++;
           if(sum<k-1)
           {
           	  if(k-1-sum>=pow(2,cnt+1)) cnt++,a[p]=pow(2,cnt),sum+=pow(2,cnt);
           	  else
           	  {
           	  	a[p]=k-1-sum;
           	  	sum=k-1;
			  }
		   }
		   else
		   {
				if(jud==0)
				{
					jud=1;
					a[p]=k+1;
					sum+=k+1;
					p++;
					a[p]=3*k+1;
					p++;
					a[p]=2*k+1;
				//	sum+=3*k+1+2*k+1;
				}
				else
				{
					a[p]=pow(2,q)*k+1;
					sum+=pow(2,q)*k+1;
					q++;
				}
			//	cout<<1<<endl;

		   }

		}
			cout<<p<<'\n';
		   for(ll i=1;i<=p;i++)cout<<a[i]<<" ";
		   cout<<'\n';
	}

	}
}