CSP初赛错题集

初赛错题集

洛谷有题

NOIP 2018

T9

给定一个含N 个不相同数字的数组，在最坏情况下，找出其中最大或最小的数，至少需要N - 1 次比较操作。则最坏情况下，在该数组中同时找最大与最小的数至少需要（A）次比较操作。（\(\lceil\rceil\)表示向上取整，\(\lfloor\rfloor\)表示向下取整）

A.⌈ 3N/2⌉-2

B.⌊3N/2⌋-2

C.2N-2

D.2N-4

解析：

如果分别找最大值、最小值，则至少都需要N-1次操作。

同时找最大最小值，有更优化的方法，如果没有学过这个算法，本题只能根据题面猜测肯定小于2N-2。需在A和B里面蒙一个，50%几率。

学过的话，按照下面的优化算法：

N为奇数时，比较次数为3*(N-1)/2 =(3N+1)/2 - 2

N为偶数时，比较次数为1 +3*(N-2)/2 = 3N/2 – 2

综合奇偶，显然答案为A

找最大最小值的优化算法：

初始值：

1. N为奇数，最大值、最小值的初始值都设为第一个元素。

2. N为偶数，将前两个元素比较，最大值初始值为大的元素，最小值初始值为小的元素。

枚举，每次两个元素（循环步长为2）

比较两个元素，分出大小。

大的元素与最大值比较，比最大值大则设为该元素。

小的元素与最小值比较，比最小值小则设为该元素。

循环结束，得到最大、最小值。

NOIP 2017

T19

一家四口人，至少两个人生日属于同一月份的概率是（）（假定每个人生日属于每个月份的概率相同且不同人之间相互独立）。

$ANS =\dfrac{41}{96} $

思路：至少有两个人的生日在同一个月，包括 2、3、4 个人的生日在同一个月三种情况，直接算比较麻烦，从反面算，再用1减去。反面是：4 个人的生日都在不同月份。

计算：

1. 分母：\(12^4\)（因为所有可能的情况是每个人的生日月份都有12种可能）

2. 分子：\(12\times11\times10\times9\)（4个人的生日都在不同月份）

3. 算出来等于 \(\frac{990}{1728}\)（自己约分）（这是反面的概率）

4. 用 1 减 \(\frac{990}{1728}\)（至少两个人生日在同一个月的概率）

T22

如下图所示，共有 13 个格子。对任何一个格子进行一次操作，会使得它自己以及与它上下左右相邻的格子中的数字改变（由 1 变 0，或由 0 变 1）。现在要使得所有的格子中的数字都变为 0，至少需要（3）次操作。

解析

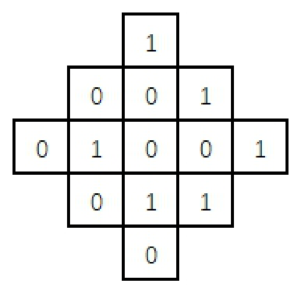
CSP-J 2019

T7

把 8 个同样的球放在 5 个同样的袋子里，允许有的袋子空着不放，问共有多少种不同的分法？（18）

提示：如果 8 个球都放在一个袋子里，无论是哪个袋子，都只算同一种分法。

解：整数拆分问题,8 拆成至多 5 个数之和(不计顺序),可按袋子个数分类讨论:

1. 1个袋子1种
2. 2个袋子4种
3. 3个袋子5种
4. 4个袋子5种
5. 5个袋子3种

共18种

T13

—些数字可以颠倒过来看，例如 \(0,1,8\) 颠倒过来还是本身，\(6\) 颠倒过来是 \(9\) , \(9\) 颠倒过来看还是 \(6\)，其他数字颠倒过来都不构成数字。

类似的，一些多位数也可以颠倒过来看，比如 \(106\) 颠倒过来是 \(901\)。假设某个城市的车牌只由 \(5\) 位数字组成，每一位都可以取\(0\) 到 \(9\)。

请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌？（\(75\)）

解析：容易发现，车牌的最中间一位只能是 \(0,1,8\) 中的一个，因为只有他们倒过来是自己本身。这个车牌同时必须是回文的，即 \(1,2\) 位必须和 \(4,5\) 位相同，第 \(1,2\) 位每位均有 \(5\) 种选法，第 \(4,5\) 位对应的只有一种，又根据乘法原理，\(5\times 5\times 3\times 1\times 1=75\)。

NOIP 2016

T6

如果开始时计算机处于小写输入状态，现在有一只小老鼠反复按照 CapsLock、字母键 A、字母键 S 和字母键 D 的顺序循环按键，即 CapsLock、A、S、D、CapsLock、A、S、D、……，屏幕上输出的第 \(81\)个字符是字母 \(D\)。

解：由题意得，\(6\) 个字母 \(A,S,D,a,s,d\) 为一个周期，第 \(81\) 个字符即 \(81\bmod 6=3\) 即 \(D\)

T18

Lucia 和她的朋友以及朋友的朋友都在某社交网站上注册了账号。下图是他们之间的关系图，两个人之间有边相连代表这两个人是朋友，没有边相连代表不是朋友。

这个社交网站的规则是：

1. 如果某人 A 向他（她）的朋友 B 分享了某张照片，那么 B 就可以对该照片进行评论；
2. 如果 B 评论了该照片，那么他（她）的所有朋友都可以看见这个评论以及被评论的照片，但是不能对该照片进行评论（除非 A 也向他（她）分享了该照片）。

现在 Lucia 已经上传了一张照片，但是她不想让 Jacob 看见这张照片，那么她可以向以下朋友 （A ）分享该照片。

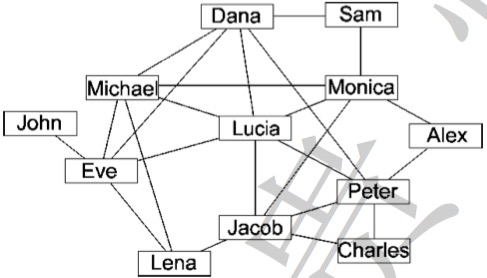
A. Dana, Michael, Eve

B. Dana, Eve, Monica

C. Michael, Eve, Jacob

D. Micheal, Peter, Monica

解：将 Lucia 与 Jacob 间长度为 2 的路径删去，即删去 Lucia - Peter - Jacob 和 Lucia - Monica - Jacob, 还剩下 Dana, Michael, Eve.

话说为什么不让Jacob看呢？

不许瑟瑟

T19

周末小明和爸爸妈妈三个人一起想动手做三道菜。小明负责洗菜、爸爸负责切菜、妈妈负责炒菜。假设做每道菜的顺序都是

1. 洗菜 10 分钟
2. 切菜 10 分钟
3. 炒菜 10 分钟。

那么做一道菜需要 30 分钟。

注意：两道不同的菜的相同步骤不可以同时进行。

例如第一道菜和第二道的菜不能同时洗，也不能同时切。那么做完三道菜的最短时间需要（50）分钟

解：如下表

10	20	30	40	50
洗1	洗2	洗3
	切1	切2	切3
		炒1	炒2	炒3

表格是什么大可爱啊啊啊

SCP 2021

T2

现有一段 24 分钟的视频文件，它的帧率是 30Hz，分辨率是 1920×1080，每帧图像都是 32 位真彩色图像，使用的视频编码算法达到了 25% 的压缩率。则这个视频文件占用的存储空间大小约是 （C）

A. 668GiB

B. 334GiB

C. 85GiB

D. 500GiB

解：\(\frac{24\times 60\text{s}\times 30\text{Hz}\times 1980\times 1080\times32\text{Bit}}{8\times 1024\times 1024\times 1024}{}\times 25\% = 85\text{GiB}\)

T3

链接器的功能是（B）

A. 把源代码转换成特定硬件平台的机器指令

B. 把机器指令组合成完整的可执行程序

C. 把源代码转换成可执行程序

D. 把高级语言翻译成低级语言

T4

第 4 题

对一个 \(n\) 个顶点，\(m\) 条边的带正权有向简单图使用 Dijkstra 算法计算 单源最短路 时，如果在使用一个可以在 \(\Theta(logn)\) 时间复杂度内查询堆内最小值、在 \(\Theta (n)\) 时间复杂度内合并两个堆、在 \(\Theta(1)\) 时间复杂度内将堆内一个元素变小、\(\Theta(\log n)\) 时间复杂度内弹出堆内最小值的堆优化 Dijkstra 算法，则整个 Dijkstra 算法的时间复杂度为 C

A. \(\Theta(n\sqrt n + m\log n)\)

B. \(\Theta((n+m)\log n)\)

C. \(\Theta(m + n\log n)\)

D. \(\Theta(m\sqrt n + n\log n)\)

解：

while 循环 \(n\) 次，每次取堆顶花费 \(\Theta(1)\) 弹出堆顶花费 \(\Theta(\log n)\)，for 共循环 \(m\) 次，每次更新堆顶花费 \(\Theta(1)\) ；共 \(n\times \Theta(1)+\Theta(\log n)+m\times \Theta(1)=\Theta(m + n\log n)\)次。

T5

具有 \(n\) 个顶点，\(m\) 条边的连通图采用邻接矩阵存储结构，进行深度优先遍历运算的时间复杂度为 （B）

A. \(\Theta (n^3)\)

B. \(\Theta (n^2)\)

C.\(\Theta (n+m)\)

D.\(\Theta (m^2)\)

解：

邻接矩阵啊喂！！！

对于每个节点，都要遍历 \(n\) 条边。

T6

下列算法中，没有运用分治思想的一项是（D）

A.归并排序算法

B.求二叉树的前序遍历

C.快速排序算法

D.求二叉树的层次遍历

T13

有 \(4\) 个结点和 \(4\) 条边的有标号简单无向图的数量是（\(15\)）

解：有 \(C_4^2​=6\) 条可能的边，选其中 \(4\) 条，即 \(C_6^4​=15\) 种。

T21

从一个 \(4\times4\) 的棋盘（不可旋转）中选取不在同一行也不在同一列上的两个方格，共有（$72 $）种方法。

每一个格子可以选 \(9\) 个格子，会重复计算一遍，故答案为 \(2\times 4\times4\times9=72\)（种）

YBT - 9

单项选择

T6

冒泡排序在（元素无序）时比较次数最多，快速排序在（元素（基本）有序）时会退化。

T7

\(10 \leq n \leq 99\)，\(n\) 两位上的数字之和为 \(a\)，令 \(n\) 分别乘 \(3,5,7,9\)，所得四个乘积的各位数之和分别仍然是 \(a\)，求 \(n\) 的个数（5）

设 \(A = 3n,B=5n,C=7n,D=9n\)，

\(\because 3n\text{的各位之和仍为}a\)

\(\therefore a,n\text{为3的倍数}\)

\(\because 9n\text{的各位之和仍为}a\)

\(\therefore a,n\text{为9的倍数}\)

\(\therefore a = 9 \text{或}18\)

\(\therefore n = 18,27,36,45,54,63,72,81,90,99\)

经验证得，\(27,54,63,72,81\) 不能满足所有条件。

故答案为 \(5\)。

T7

\(15\) 张卡片，每张卡片上有三个不同的汉字，没有两张卡片上的汉字完全相同，任意六张中，一定有两张卡片上含有相同的汉字，求最多有（35）个不同的汉字。

第一至第六张，设第一和第二张有汉字重复；

第二至第七张，设第二和第三张有汉字重复；

第十至第十五张，设第十张和第十一张有汉字重复；

总共重复了十个汉字，故有 \(45 - 10 = 35\)个不重复的汉字。

阅读理解

1.

const int N = 2e5;
int a[N];

将2e5修改为2e10，可以正常运行（F）

会爆数组空间，int类型数组总和不可超过1e7。

2.

//链式前向星存图
int h[N];
void spfa()
{
    for (int i = h[t];____;i = next[i])
}
int main()
{
    memset(h, -1, sizeof(h));
}

______处应填（C）

A.i = 0

B.i > 0

C.i != -1

D.i > -1

int a[N];
sort(a, a + n);
int x = _____; //x 表示数组 a 的最大值

_____ -> a[n - 1]

YBT - 10

单项选择

T1

甲：6 鼠标或 2 键盘 / h

乙：4 鼠标或 4 键盘 / h

求 6 h 最多生产多少套键鼠套装？（不必一小时只生产键盘或鼠标）（27）

解：

模拟几次后易看出，键鼠套装的套数取决于键盘的个数，使用贪心思想，令乙生产 6 小时键盘，得到 24 个键盘，甲生产 4.5 小时鼠标，1.5 小时键盘，得到 27 个鼠标，3 个键盘，共 27 套键鼠套装。

思想即为令甲先生产与乙配套的鼠标，剩下时间尽可能的生产多的键鼠套装。

T4

下列不属于计算机人工智能领域的是（A.在线买票）

A.在线买票

B.医疗诊断

C.智能机器人

D.机器翻译

在线买票属于电子商务。

YBT - 12

单项选择

T5

以下数据用 int 表示最恰当的是（D）

A. 宇宙中原子数目

B. 蓝鲸体重（单位 t）

C. 小明身高（单位 m）

D. 一个学校的教师人数

T6

用同等规模的双核和单核 CPU 编写程序，运行时间（无明显差异）

双核和单核的区别在于多任务处理

阅读理解

1.

（统计逆序对）归并排序中，msort(1, n); 改为 msort(1, n + 1);，逆序对会增加，a[1] 到 a[n]也会改变。

YBT - 13

单项选择

T3

输入 www.cisco.com 不可访问，但输入 IP 地址仍可访问，故障归咎于（DNS）

未能解析域名，DNS 的锅

T6

分治法求解需满足的条件

1. 子问题类型相同

2. 子问题不能重复

3. 子问题可以合并

4. 原问题和子问题采用相同方法求解

T8

堆的形状是一棵（完全二叉树）

T12

\[\begin{cases}
x\bmod 4 = 3\\
x\bmod 6=5\\
x\bmod 15 = 14\\
150\leq x\leq 200
\end{cases}
\]

不难看出，\(x = k\times\text{lcm}(4,6,15)-1,(k\in N^*)\)

易得 \(x=60\times 3-1=179\)

YBT - 14

单项选择

T2

存取速度：寄存器 > 高速缓存 > 内存 > 外存。

T9

五个人，每人制造 100 架纸飞机，一包纸有四张，一张纸可制造 7 架纸飞机，不能借纸，不能提前裁纸，老板可拆开一包纸，分给员工。问至少要买几包纸。

每个员工需要 \(\lceil\frac{100}{7}\rceil = 15\) 张纸，共 \(15 \times 5 = 75\) 张。要买 \(\lfloor \frac{75}{4} \rfloor = 19\) 包。

T10

田忌赛马：赢+10，输 -10，平 +0；

	1	2	3	4	5	6	7	8	9	10
田忌	100	95	90	85	80	75	70	65	60	55
齐王	98	97	92	88	85	81	55	50	44	40

田忌第四匹对齐王第六匹，\(+10\)。

田忌第五匹对齐王第五匹，\(-10\)。

田忌第 \(i\) 匹对齐王第 \(i + 1\) 匹，\(+10 \times 7 - 10 = 60\)

故最多赢 \(60\) 。

T12

汉诺塔，A 只能到 B，B 只能到 C，C 只能到 A。

A 柱上有三个盘子，移动到 C 柱上的次数：\(21\)

T13

有五本不同的书摆放在书架上，求每一本书都不在原来位置的排列数

（\(44\)）

错位排列（容斥）

记 \(n\) 封信的错位重排数为 \(D_n\)。

则 \(D_1=0,D_2=1,D_n=(n-1)(D_{n-2}+D_{n-1})\)

\(D_n\)的前几项：\(D_1=0,D_2=1,D_3=2,D_4=9,D_5=44\)

T14

字符串 “zhangnahz” 本质不同的子串个数（\(42\)）

空串：\(1\) 个；

长度为 \(1\)：\(5\) 个

长度为 \(2\) 到 \(9\) ：\(8+7+6+5+4+3+2+1=36\) 个

共 \(1+5+36 = 42\) 个。

阅读理解

1.

int a,b;
cin >> a >> b;
int ans = 1;
while(b)
{
    if(b & 1) ans *= a;
    a *= a;
    b >>= 1;
}
cout << ans;

输入 \(a = 10,b=10\)，能得到正确答案（\(F\)）。

\(10_{(10)}=1010{(2)}\)

\(ans = 10^2 \times 10^8 = 10^{12}\)

爆 int 了。

2.

void bubble_sort(int a[],int n)
{
    for (int i = 1; i <= n - 1; ++i)
    {
        int index = i;
        for (int j = i + 1; k <= n;++j)
        {
            if (a[j] < a[index]) index = j;
            if (index != i)
            {
                swap(a[index],a[i]);
            }
        }
    }
}

若将 if (index != i)改为if (1)，不会影响程序运行结果（\(T\)）

当 index == k时，交换无影响。

将while (i <= mid) b[k++] = a[i++];与 while (j <= r) b[k++] = a[j++];交换，程序运行结果不变（\(T\)）。

3.

void merge_sort(int l, int r)
{
    if (l == r) return;
    int mid = (l + r) >> 1;
    merge_sort(l, mid); mergesort(mid + 1,r);
    int i = l, j = mid + 1, k = l;
    while (i <= mid && j <= r)
    {
        if (a[i] < a[j])
        {
            ans += j - k;
            b[k++] = a[j++];
        }
        else
            b[k++] = a[i++];
    }
    while (i <= mid) b[k++] = a[i++];
    while (j <= r) b[k++] = a[j++];
    for (int i = l; i <= r; ++i) a[i] = b[i];
}

归并排序——百度百科

归并操作[\(O(n\log n)\)]的工作原理如下：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

4. 重复步骤 3 直到某一指针超出序列尾

5. 将另一序列剩下的所有元素直接复制到合并序列尾

YBT - 15

单项选择

T3

\(200\text{Mbps}\) 的宽带下载大小为 \(2\text{GByte}\) 的文件极限最快大约需要（\(81.92\)）秒

\[\dfrac{2\times 1024\times 1024\times 1024\times 8}{200\times 1024\times 1024} = \frac{2^{34}}{2^{21}\times 100}
\]

T4

IP地址 \(10.20.220.222\)，子网掩码 \(255.255.192.0\)，网络号为（\(10.20.192.0\)）

\[\begin{aligned}
&\,\,\,10.\,\,\,20.220.222&\\
\&\,&255.255.192.\,\,\,\,\,\,0&\\
&\,\,\,10.\,\,\,20.192.\,\,\,\,\,\,0
\end{aligned}
\]

和 \(255\) 相与 得原数，和 \(192\) 相与得 \(192\)。

T7

下列 （A）不是 STL 序列式容器

A. set

B. list

C. vector

D. deque

set 本质上是一棵平衡二叉树。

T8

cin，cout 属于（A）

A. 类

B. 结构体

C. 函数

D. 变量

T9

同一个小数，用 double 存和用 float 存，（D）

A. double 大

B. float 大

C. 相等

D. 不确定

double 和 float 只是精度问题，并不和大小相关。

T10

main 函数中 用 malloc() 开辟了数组空间，在（B）

A. 栈空间

B. 堆空间

C. 全局区（静态区）

D. 都有可能

自开空间在堆空间

T12

4个人过河，过河所需时间分别是1,2,5,10，每次过两人，速度由慢者决定，已过河中的一人回，速度由这个人决定，问过河所需最短时间（）。

A.19 B.18 C.17 D.16

答案为C。

综上，这种问题，我们先考虑将最慢的两人送去，分为两种情况

1.让最快的两个人过去，其中一人回来，再让最慢的两个过去，先去的两人中另一人再回来。

2.让最快的和最慢的过去，最快的回来，再让最快的和第二慢的过去，最快的再回来

以上情况为 ≥4 人的情况，当人数 <4时，直接分情况讨论即可。

平方和公式

\[\sum_{i = 1}^ni^2 = \frac{n(n + 1)(2n+1)}{6}
\]

证明:

\[\begin{aligned}
\because \sum_{i=1}^n((i+1)^3-i^3)=&2^3-1^3+3^3-2^3+\cdots +(n+1)^3-n^3\\
=&(n+1)^3-1\\
\end{aligned}\]

\[\because (n+1)^3=n^3+3n^2+3n+1
\]

\[\therefore(n+1)^3-n^3=3n^2+3n+1
\]

\[\begin{aligned}
\therefore (n+1)^3-1&=\sum_{i=1}^n 3i^2+3i+1\\
(n+1)^3-1&=3\sum_{i=1}^n i^2+3\sum_{i=1}^ni+\sum_{i=1}^n1\\
n^3+3n^2+3n&=3\sum_{i=1}^ni^2+3\times\frac{(1+n)n}{2}+n\\
3\sum_{i=1}^ni^2&=n^3+3n^2+3n-3\times\frac{(1+n)n}{2}-n\\
\sum_{i=1}^ni^2&=\frac{n^3}3+n^2+\frac3 2n-\frac{(1+n)n}{2}\\
&=\frac{2n^3+6n^2+9n-3n^2-3n}{6}\\
&=\frac{2n^3+3n^2+6n}{6}\\
&=\frac{n(2n^2+3n+6)}{6}\\
&=\frac{n(n+1)(2n+1)}{6}\\
\end{aligned}
\]

T14

\(x\bmod3=2,x\bmod 5 = 3, x\bmod 7 = 2\)

求第五个 \(x\)

（\(443\)）

CRT

用于求解如下形式的方程组

\[\begin{cases}
x&\equiv &a_1(\bmod\ n_1)\\
x&\equiv &a_2(\bmod\ n_2)\\
&\vdots\\
x&\equiv &a_k(\bmod\ n_k)\\
\end{cases}
\]

1. 计算所有模数的积 \(n\)

2. 对于第 \(i\) 个方程：

• 计算 \(m_i=n/n_i\)

• 计算 \(m_i\) 在模 \(n_i\) 意义下的逆元 \(m_i^{-1}\)

• 计算 \(c_i=m_im_i^{-1}\) （不对 \(n_i\) 取模）

1. 方程组在模 \(n\) 意义下的唯一解为：\(x = \sum_{i=1}^ka_ic_i(\bmod\,n)\)

解：

\[\begin{cases}
x\equiv 2(\bmod\ 3)\\
x\equiv 3(\bmod\ 5)\\
x\equiv 2(\bmod\ 7)\\
\end{cases}
\]

\[\begin{cases}
n=105\\
m_1=35,m_2=21,m_3=15\\
c_1=35\times2,c_2=21,c_3=15\\
\end{cases}
\]

\[x\equiv2\times 70+3\times21+2\times15\equiv233\equiv23(\bmod\ 105)
\]

第一个解为 \(23\)，第 \(k\) 个解为 \(23 + n\times(k-1)\)

\(ans = 23+105\times 4=443\)

阅读程序

1.

将scanf("%d\n", &a);中的 \n去掉，下一行的gets(s);读取结果不变。（\(F\)）

scanf 会把空格和换行丢弃在读入序列中，因此，去掉\n后gets(s);将读取\n。

2.

C++ 语言中，struct 默认是 public 的，而 class 默认是 private 的。（\(T\)）

3.

memset 函数是以（\(1\)）个字节为一组进行设置的。

4.

void print(int *a, int （1）);

已知（1）作为一个int类型参与函数，且（1）的值在函数中不被改变，则（1）中不能填（B）

A. cnt

B. *cnt

C. &cnt

D. cons cnt

*cnt 只传进 cnt 的地址。