63.不同路径II

目录

• 63.不同路径Ⅱ
  • 题目
  • 题解

63.不同路径Ⅱ

题目

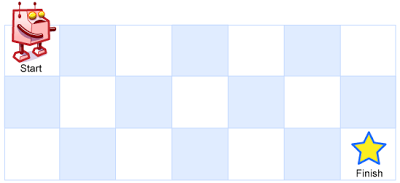
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

m == obstacleGrid.length

n == obstacleGrid[i].length

1 <= m, n <= 100

obstacleGrid[i][j] 为 0 或 1

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/unique-paths-ii

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

这道题和之前做的62题是非常相似的，只不过多了一个路障。

62题的dp递推式是dp[i][j] = dp[i][j-1] + dp[j-1][i];

这道题依然适用，只不过需要考虑有路障的情况

初始化时，有路障obstacleGrid[i][j]==1的地方dp[i][j]=0，表示没办法达到

还需要考虑的就是i=0或者j=0时，路上有路障的话，那么是没办法到达终点的。处理办法有两种

1.dp[i][j] = dp[i][j-1]或者dp[i][j] = dp[i-1][j]

2.当obstacleGrid[i][j]==0时，dp[i][j]初始化为1

我选择第一种做法

代码

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m= obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int [][] dp = new int[m][n];
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(obstacleGrid[i][j]==1){
                    dp[i][j]=0;
                }else if(i==0&&j==0){
                    dp[0][0] =1;
                }else if(i==0){
                    dp[i][j] = dp[i][j-1];
                }else if(j==0){
                    dp[i][j] = dp[i-1][j];
                }else{
                    dp[i][j] = dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
}