Python数模笔记-Sklearn（2）样本聚类分析

1、分类的分类

　　分类的分类？没错，分类也有不同的种类，而且在数学建模、机器学习领域常常被混淆。

　　首先我们谈谈有监督学习（Supervised learning）和无监督学习（Unsupervised learning），是指有没有老师，有没有纪委吗？差不多。有老师，就有正确解法，就有标准答案；有纪委，就会树学习榜样，还有反面教材。

　　有监督学习，是指样本数据已经给出了正确的分类，我们通过对正确分类的样本数据进行学习，从中总结规律，获取知识，付诸应用。所以，监督学习的样本数据，既提供了特征值又提供了目标值，通过回归（Regression）、分类（Classification）学习特征与目标之间的关系。回归是针对连续变量、连续数据，分类是针对离散变量和布尔变量（0-1）。

　　无监督学习，是指样本数据没有提供确定的分类属性，没有老师，没有标准答案，样本数据中只有样本的特征值而没有目标值，只能通过样本数据自身的特征一边摸索一边自我学习，通过聚类（Clustering）方法来寻找和认识对象的相似性。

　　所以，我们说到分类时，其实有时是指分类（Classification），有时则是指聚类（Clustering）。

　　有监督学习有老师，就有正确答案。虽然有时也会有模糊地带，但总体说来还是有判定标准、有是非对错的，只要与标准答案不一致就会被认为判断错误。

　　无监督学习则不同，可以有不同的分类方法、不同的分类结果，通常只有相对的好坏而没有绝对的对错。甚至连分类结果的好坏也是相对的，要根据实际需要实际情况进行综合考虑，才能评价分类结果的好坏。谁能说人应该分几类，怎么分更合理呢？

2、聚类分析

2.1 聚类的分类

　　聚类是从数据分析的角度，对大量的、多维的、无标记的样本数据集，按照样本数据自身的相似性对数据集进行分类。大量，是指样本的数量大；多维，是指每个样本都有很多特征值；无标记，是指样本数据对于每个样本没有指定的类别属性。

　　需要说明的是，有时样本数据带有一个或多个分类属性，但那并不是我们所要研究的类别属性，才会被称为无监督学习。比如说，体能训练数据集中每个样本都有很多特征数据，包括性别、年龄，也包括体重、腰围、心率和血压。性别、年龄显然都是样本的属性，我们也可以根据性别属性把样本集分为男性、女性两类，这当然是有监督学习；但是，如果我们是打算研究这些样本的生理变化与锻炼的关系，这是性别就不定是唯一的分类属性，甚至不一定是相关的属性了，从这个意义上说，样本数据中并没有给出我们所要进行分类的类别属性。

　　至于聚类的分类，是针对研究对象的不同来说的。把样本集的行（rows）作为对象，考察样本的相似度，将样本集分成若干类，称为 Q型聚类分析，属于样本分类。把样本集的列（columns）作为对象，考察各个特征变量之间的关联程度，按照变量的相关性聚合为若干类，称为 R型聚类分析，属于因子分析。

2.2 Q型聚类分析（样本聚类）

　　Q 型聚类分析考察样本的相似度，将样本集分成若干类。我们需要综合考虑样本各种特征变量的数值或类型，找到一种分类方法将样本集分为若干类，使每一类的样本之间具有较大的相似性，又与其它类的样本具有较大的差异性。通常是根据不同样本之间的距离远近进行划分，距离近者分为一类，距离远者分成不同类，以达到“同类相似，异类相异”。

　　按照相似性分类，首先就要定义什么是相似。对于任意两个样本，很容易想到以样本间的距离作为衡量相似性的指标。在一维空间中两点间的距离是绝对值：d(a,b)=abs[x(a)-x(b)]；二维空间中两点间的距离，我们最熟悉的是欧几里德（Euclid）距离：d(a,b)=sqrt[(x1(a)-x1(b))**2+(x2(a)-x2(b))**2]，欧式距离也可以拓展到多维空间。

　　除了欧式距离之外，还有其它度量样本间距的方案，例如闵可夫斯基距离（Minkowski）、切比雪夫距离（Chebyshev）、马氏距离（Mahalanobis）等。这些距离的定义、公式和使用条件，本文就不具体介绍了。世界是丰富多彩的，问题是多种多样的，对于特殊问题有时就要针对其特点采用特殊的解决方案。

　　进而，对于两组样本G1、G2，也需要度量类与类之间的相似性程度。常用的方法有最短距离法（Nearest Neighbor or Single Linkage Method）、最长距离法（Farthest Neighbor or Complete Linkage Method）、重心法（Centroid Method）、类均值法（Group Average Method）、离差平方和法（Sum of Squares Method）。

　　另外，处理实际问题时，在计算距离之前要对数据进行标准化、归一化，解决不同特征之间的统一量纲、均衡权重。

3、SKlearn 中的聚类方法

　　SKlearn 工具包提供了多种聚类分析算法：原型聚类方法（Prototype）、密度聚类方法（Density）、层次聚类方法（Hierarchical）、模型聚类（Model），等等，原型聚类方法又包括 k均值算法（K-Means）、学习向量量化算法（LVQ）、高斯混合算法（Gaussian Mixture）。详见下表。

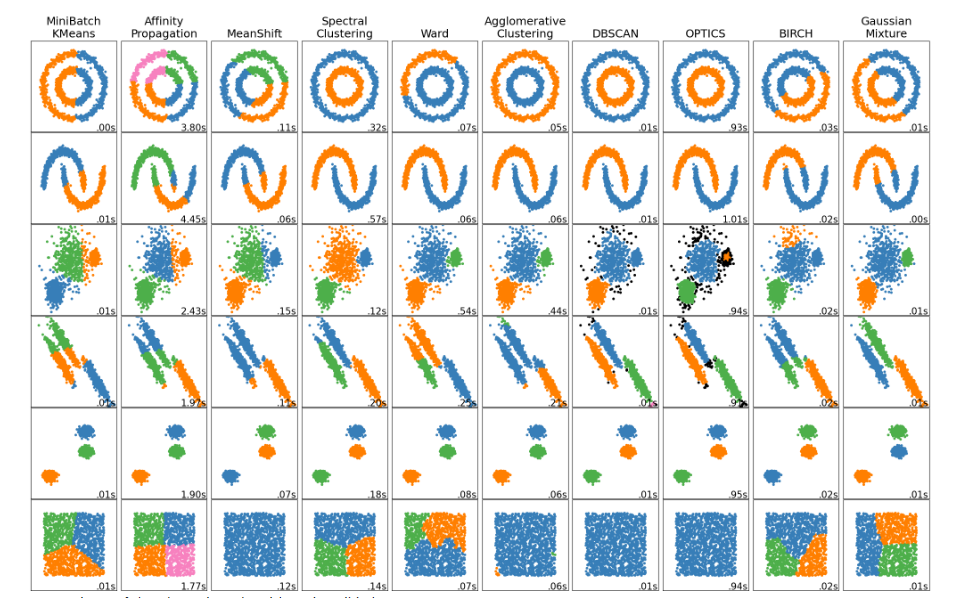
　　为什么会有这么多方法和算法呢？因为特殊问题需要针对其特点采用特殊的解决方案。看看下面这张图，就能理解这句话了，也能理解各种算法都是针对哪种问题的。SKlearn 还提供了十多个聚类评价指标，本文就不再展开介绍了。

4、K-均值（K-Means）聚类算法

　　K-均值聚类算法，是最基础的、应用最广泛的聚类算法，也是最快速的聚类算法之一。

4.1 原理和过程

　　K-均值聚类算法以最小化误差函数为目标将样本数据集分为 K类。

　　K-均值聚类算法的计算过程如下：

设定 K 个类别的中心的初值；
计算每个样本到 K个中心的距离，按最近距离进行分类；
以每个类别中样本的均值，更新该类别的中心；
重复迭代以上步骤，直到达到终止条件（迭代次数、最小平方误差、簇中心点变化率）。

　　K-均值聚类算法的优点是原理简单、算法简单，速度快，聚类效果极好，对大数据集具有很好的伸缩性。这些优点特别有利于初学者、常见问题。其缺点是需要给定 K值，对一些特殊情况（如非凸簇、特殊值、簇的大小差别大）的性能不太好。怎么看这些缺点？需要给定 K值的问题是有解决方法的；至于特殊情况，已经跟我们没什么关系了。

4.2 SKlearn 中 K-均值算法的使用

　　sklearn.cluster.KMeans 类是 K-均值算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html#sklearn.cluster.KMeans

　　

class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')

KMeans 的主要参数：

n_clusters: int,default=8　　K值，给定的分类数量，默认值 8。
init：{‘k-means++’, ‘random’}　　初始中心的选择方式，默认'K-means++'是优化值，也可以随机选择或自行指定。
n_init：int, default=10　　以不同的中心初值多次运行，以降低初值对算法的影响。默认值 10。
max_iter：int, default=300　　最大迭代次数。默认值 300。
algorithm：{“auto”, “full”, “elkan”}, default=”auto”　　算法选择，"full"是经典的 EM算法，"elkan"能快速处理定义良好的簇，默认值 “auto"目前采用"elkan"。

KMeans 的主要属性：

clustercenters：每个聚类中心的坐标
labels_： 每个样本的分类结果
inertia_： 每个点到所属聚类中心的距离之和。

4.3 sklearn.cluster.KMeans 用法实例

from sklearn.cluster import KMeans  # 导入 sklearn.cluster.KMeans 类

import numpy as np

X = np.array([[1,2], [1,4], [1,0], [10,2], [10,4], [10,0]])

kmCluster = KMeans(n_clusters=2).fit(X)  # 建立模型并进行聚类，设定 K=2

print(kmCluster.cluster_centers_)  # 返回每个聚类中心的坐标

#[[10., 2.], [ 1., 2.]]  # print 显示聚类中心坐标

print(kmCluster.labels_)  # 返回样本集的分类结果

#[1, 1, 1, 0, 0, 0]  # print 显示分类结果

print(kmCluster.predict([[0, 0], [12, 3]]))  # 根据模型聚类结果进行预测判断

#[1, 0]  # print显示判断结果：样本属于哪个类别

　　例程很简单，又给了详细注释，就不再解读了。核心程序就是下面这句：

　　kMeanModel = KMeans(n_clusters=2).fit(X)

4.4 针对大样本集的改进算法：Mini Batch K-Means

　　对于样本集巨大的问题，例如样本量大于 10万、特征变量大于100，K-Means算法耗费的速度和内存很大。SKlearn 提供了针对大样本集的改进算法 Mini Batch K-Means，并不使用全部样本数据，而是每次抽样选取小样本集进行 K-Means聚类，进行循环迭代。Mini Batch K-Means 虽然性能略有降低，但极大的提高了运行速度和内存占用。　　　　

　　class sklearn.cluster.MiniBatchKMeans 类是算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/generated/sklearn.cluster.MiniBatchKMeans.html#sklearn.cluster.MiniBatchKMeans

　　

class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=100, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)

MiniBatchKMeans 与 KMeans不同的主要参数是：

batch_size: int, default=100　　抽样集的大小。默认值 100。

　　Mini Batch K-Means 的用法实例如下：

from sklearn.cluster import MiniBatchKMeans # 导入 .MiniBatchKMeans 类

import numpy as np

X = np.array([[1,2], [1,4], [1,0], [4,2], [4,0], [4,4],

              [4,5], [0,1], [2,2],[3,2], [5,5], [1,-1]])

# fit on the whole data

mbkmCluster = MiniBatchKMeans(n_clusters=2,batch_size=6,max_iter=10).fit(X)

print(mbkmCluster.cluster_centers_) # 返回每个聚类中心的坐标

# [[3.96,2.41], [1.12,1.39]] # print 显示内容

print(mbkmCluster.labels_)  # 返回样本集的分类结果

#[1 1 1 0 0 0 0 1 1 0 0 1]  # print 显示内容

print(mbkmCluster.predict([[0,0], [4,5]]))  # 根据模型聚类结果进行预测判断

#[1, 0]  # 显示判断结果：样本属于哪个类别

5、K-均值算法例程

5.1 问题描述

-　　聚类分析案例—我国各地区普通高等教育发展状况分析，本问题及数据来自：司守奎、孙兆亮，数学建模算法与应用（第2版），国防工业出版社。

　　问题的原始数据来自《中国统计年鉴，1995》和《中国教育统计年鉴，1995》，给出了各地区10 项教育发展数据。我国各地区普通高等教育的发展状况存在较大的差异，请根据数据对我国各地区普通高等教育的发展状况进行聚类分析。

5.2 Python 程序



# Kmeans_sklearn_v1d.py

# K-Means cluster by scikit-learn for problem "education2015"

# v1.0d: K-Means 聚类算法（SKlearn）求解：各地区高等教育发展状况-2015 问题

# 日期：2021-05-10

#  -*- coding: utf-8 -*-

import numpy as np

import pandas as pd

from sklearn.cluster import KMeans, MiniBatchKMeans

# 主程序

def main():

    # 读取数据文件

    readPath = "../data/education2015.xlsx"  # 数据文件的地址和文件名

    dfFile = pd.read_excel(readPath, header=0)  # 首行为标题行

    dfFile = dfFile.dropna()  # 删除含有缺失值的数据

    # print(dfFile.dtypes)  # 查看 df 各列的数据类型

    # print(dfFile.shape)  # 查看 df 的行数和列数

    print(dfFile.head())

    # 数据准备

    z_scaler = lambda x:(x-np.mean(x))/np.std(x)  # 定义数据标准化函数

    dfScaler = dfFile[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']].apply(z_scaler)  # 数据归一化

    dfData = pd.concat([dfFile[['地区']], dfScaler], axis=1)  # 列级别合并

    df = dfData.loc[:,['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']]  # 基于全部 10个特征聚类分析

    # df = dfData.loc[:,['x1','x2','x7','x8','x9','x10']]  # 降维后选取 6个特征聚类分析

    X = np.array(df)  # 准备 sklearn.cluster.KMeans 模型数据

    print("Shape of cluster data:", X.shape)

    # KMeans 聚类分析(sklearn.cluster.KMeans)

    nCluster = 4

    kmCluster = KMeans(n_clusters=nCluster).fit(X)  # 建立模型并进行聚类，设定 K=2

    print("Cluster centers:\n", kmCluster.cluster_centers_)  # 返回每个聚类中心的坐标

    print("Cluster results:\n", kmCluster.labels_)  # 返回样本集的分类结果

    # 整理聚类结果

    listName = dfData['地区'].tolist()  # 将 dfData 的首列 '地区' 转换为 listName

    dictCluster = dict(zip(listName,kmCluster.labels_))  # 将 listName 与聚类结果关联，组成字典

    listCluster = [[] for k in range(nCluster)]

    for v in range(0, len(dictCluster)):

        k = list(dictCluster.values())[v]  # 第v个城市的分类是 k

        listCluster[k].append(list(dictCluster.keys())[v])  # 将第v个城市添加到 第k类

    print("\n聚类分析结果(分为{}类):".format(nCluster))  # 返回样本集的分类结果

    for k in range(nCluster):

        print("第 {} 类：{}".format(k, listCluster[k]))  # 显示第 k 类的结果

    return

if __name__ == '__main__':

    main()

5.3 程序运行结果

   地区    x1   x2   x3    x4   x5   x6     x7    x8    x9    x10

0  北京  5.96  310  461  1557  931  319  44.36  2615  2.20  13631

1  上海  3.39  234  308  1035  498  161  35.02  3052  0.90  12665

2  天津  2.35  157  229   713  295  109  38.40  3031  0.86   9385

3  陕西  1.35   81  111   364  150   58  30.45  2699  1.22   7881

4  辽宁  1.50   88  128   421  144   58  34.30  2808  0.54   7733

Shape of cluster data: (30, 10)

Cluster centers:

 [[ 1.52987871  2.10479182  1.97836141  1.92037518  1.54974999  1.50344182

   1.13526879  1.13595799  0.83939748  1.38149832]

 [-0.32558635 -0.28230636 -0.28071191 -0.27988803 -0.28228409 -0.28494074

   0.01965142  0.09458383 -0.26439737 -0.31101153]

 [ 4.44318512  3.9725159   4.16079449  4.20994153  4.61768098  4.65296699

   2.45321197  0.4021476   4.22779099  2.44672575]

 [ 0.31835808 -0.56222029 -0.54985976 -0.52674552 -0.33003935 -0.26816609

  -2.60751756 -2.51932966  0.35167418  1.28278289]]

Cluster results:

 [2 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 3]

聚类分析结果(分为4类):

第 0 类：['上海', '天津']

第 1 类：['陕西', '辽宁', '吉林', '黑龙江', '湖北', '江苏', '广东', '四川', '山东', '甘肃', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '内蒙古', '河南', '广西', '宁夏', '贵州']

第 2 类：['北京']

第 3 类：['西藏', '青海']

版权说明：

本文中案例问题来自：司守奎、孙兆亮，数学建模算法与应用（第2版），国防工业出版社。

本文内容及例程为作者原创，并非转载书籍或网络内容。