Pytorch_Part6_正则化
VisualPytorch beta发布了!
功能概述:通过可视化拖拽网络层方式搭建模型,可选择不同数据集、损失函数、优化器生成可运行pytorch代码
扩展功能:1. 模型搭建支持模块的嵌套;2. 模型市场中能共享及克隆模型;3. 模型推理助你直观的感受神经网络在语义分割、目标探测上的威力;4.添加图像增强、快速入门、参数弹窗等辅助性功能
修复缺陷:1.大幅改进UI界面,提升用户体验;2.修改注销不跳转、图片丢失等已知缺陷;3.实现双服务器访问,缓解访问压力
访问地址:http://visualpytorch.top/static 或 http://114.115.148.27/static
发布声明详见:https://www.cnblogs.com/NAG2020/p/13030602.html
一、正则化之weight_decay
1. Regularization:减小方差的策略
误差可分解为:偏差,方差与噪声之和。即误差 = 偏差 + 方差 + 噪声之和
偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力
方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界
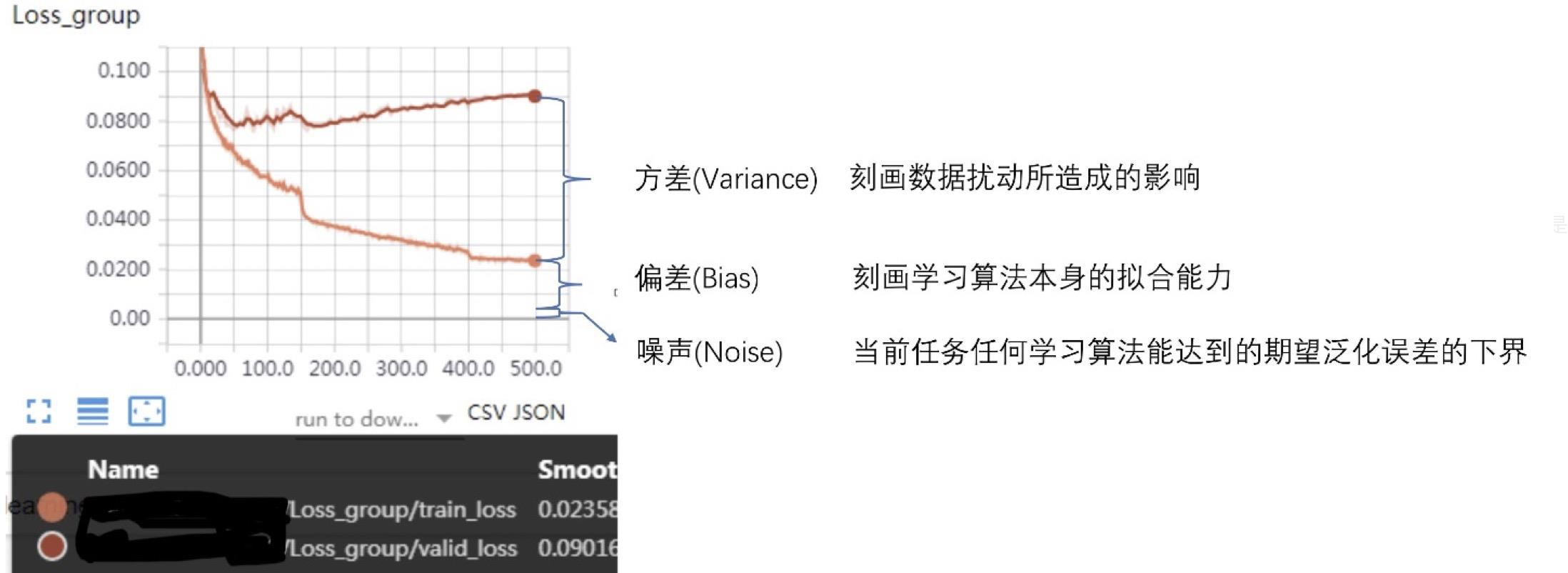
准确地来说方差指的是不同针对 不同 数据集的预测值期望的方差,而非训练集和测试集Loss的差异。
2. 损失函数:衡量模型输出与真实标签的差异
损失函数(Loss Function):\(Loss = f(\hat y , y)\)
代价函数(Cost Function):\(Cost = \frac{1}{N}\sum_i f(\hat y_i, y_i)\)
目标函数(Objective Function):\(Obj = Cost + Regularization\)
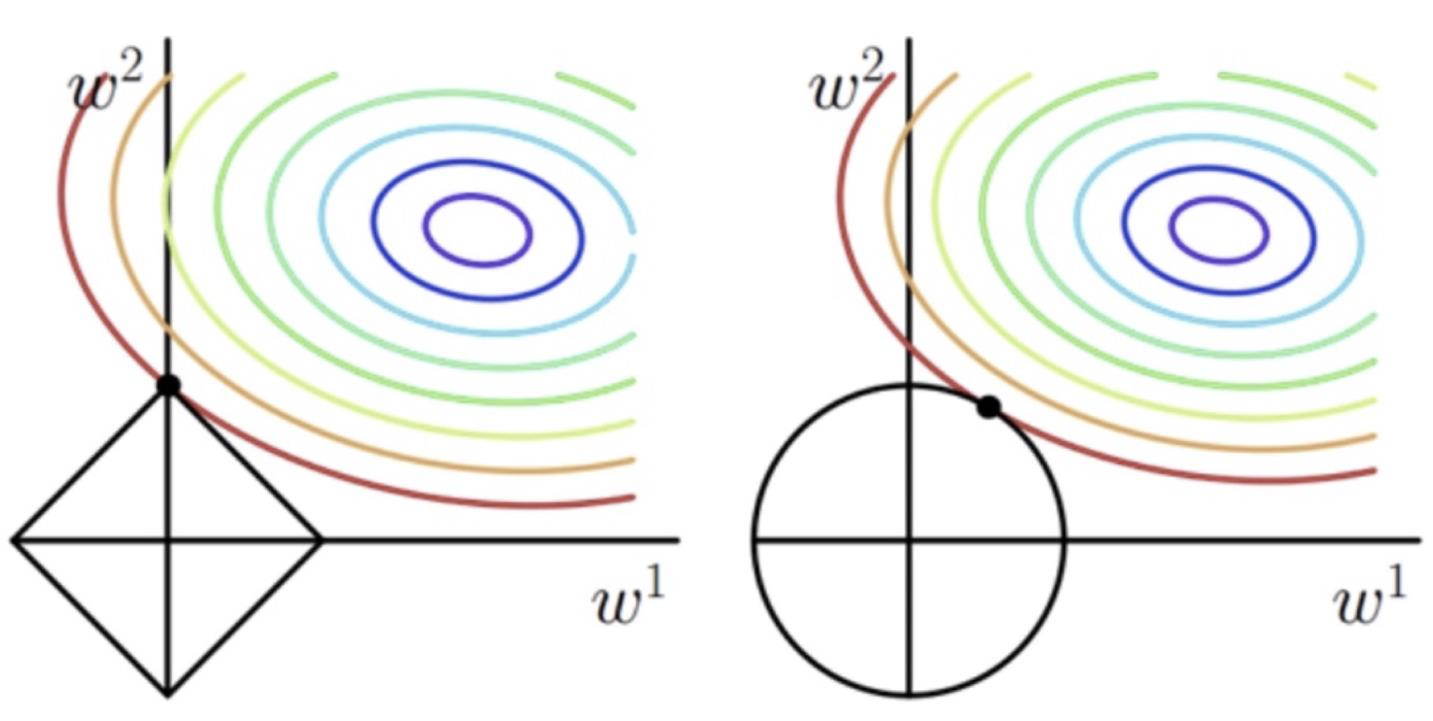
L1 Regularization: \(\sum_i |w_i|\) 因为常在坐标轴(顶点)上取极值,容易训练出稀疏参数
L2 Regularization: \(\sum_i w_i^2\) \(w_{i+1} = w_i - Obj' = w_i - (\frac{\partial Loss}{\partial w_i}+\lambda * w_i) = w_i(1-\lambda) - \frac{\partial Loss}{\partial w_i}\) ,因此常被称为权重衰减
3. 以简单的三层感知机为例
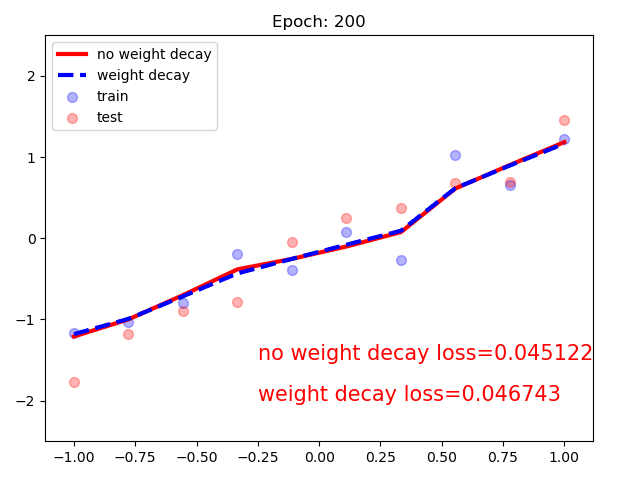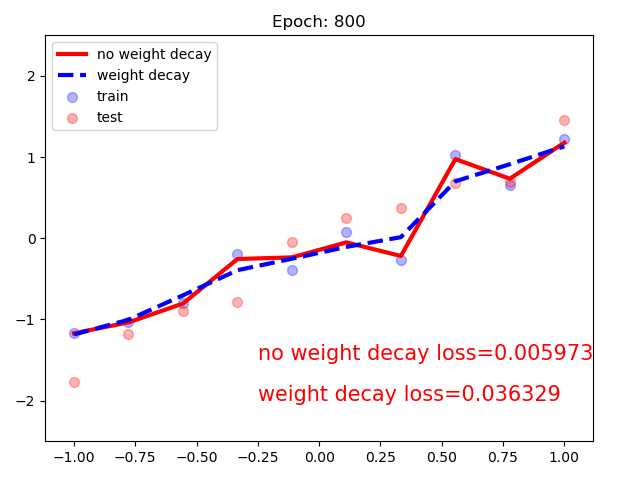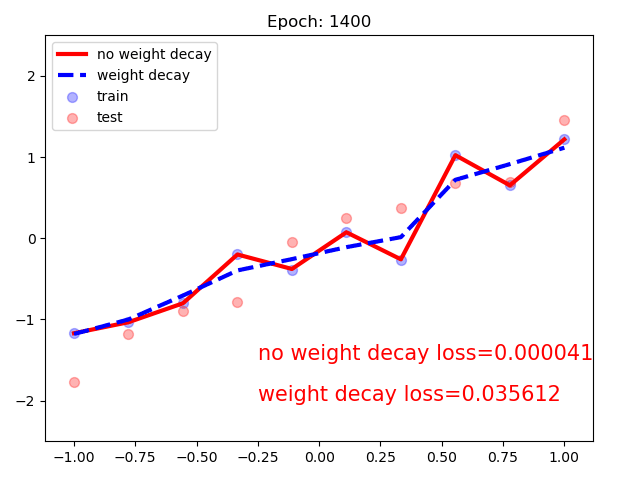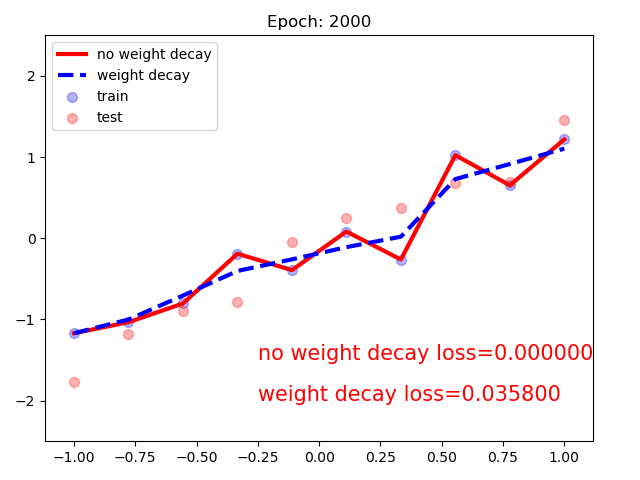
同时构建使用weight_dacay和没有的模型:可以看到,随着训练次数增加,不含正则项的模型loss趋于0.
# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):
w = 1.5
train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
return train_x, train_y, test_x, test_y
train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))
# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
def __init__(self, neural_num):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)
# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
# 包含了weight_decay
# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()
# ============================ step 5/5 迭代训练 ============================
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
# forward
pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_wdecay.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_wdecay.step()
...
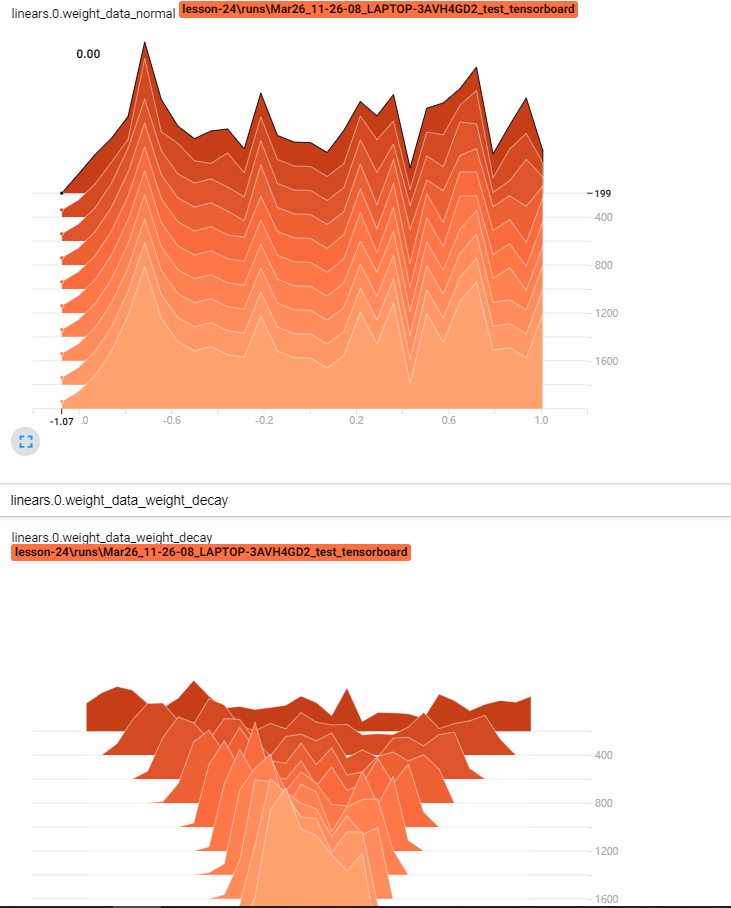
通过tensorborad查看参数变化,可以明显看出使用L2的模型参数更集中:
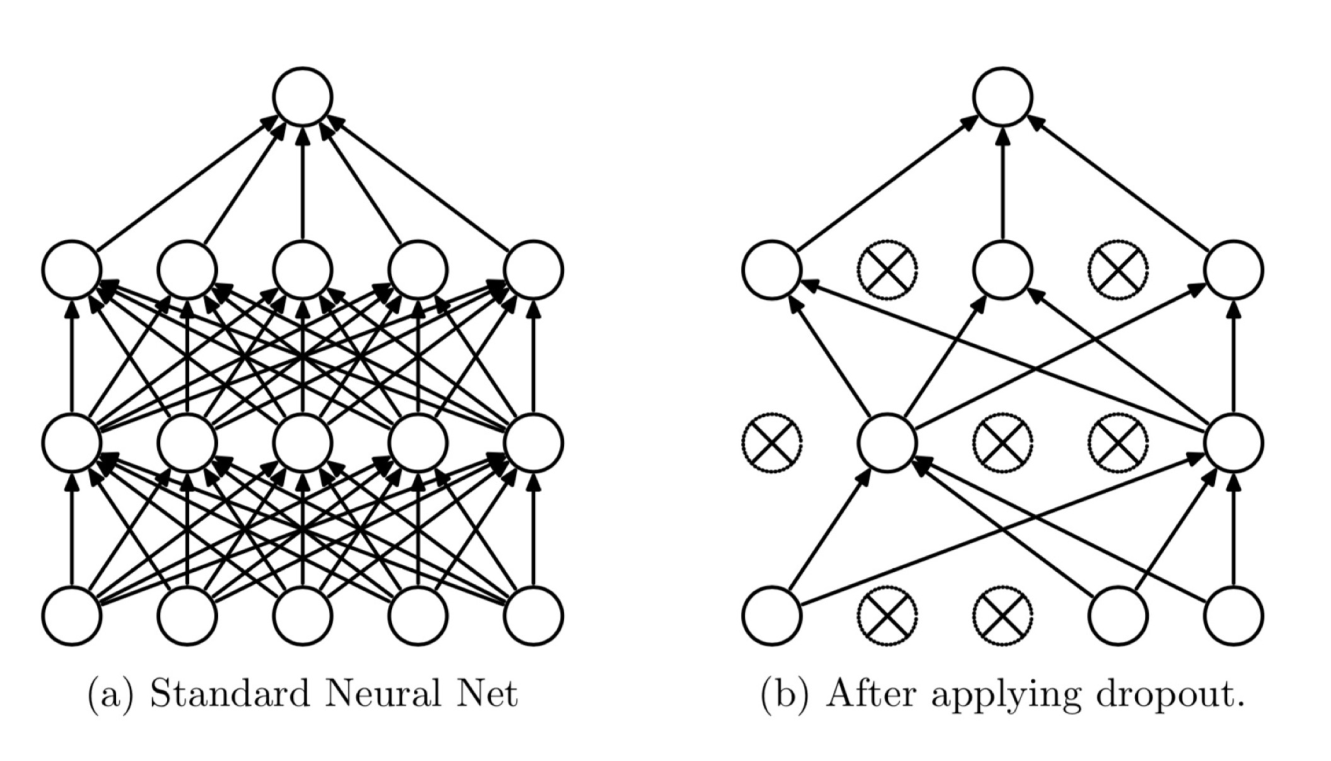
二、 正则化之Dropout
1. 随机:dropout probability
失活:weight = 0
指该层任何一个神经元都有prob的可能性失活,而非有prob的神经元会失活。
2. 带来以下三种影响:
- 特征依赖性降低
- 权重数值平均化
- 数据尺度减小
假设prob = 0.3,在测试时不使用dropout,为了抵消这种尺度上的变化,需要在训练期间对权重除 \((1-p)\)
Test: \(100 = \sum_{100} W_x\)
Train: \(70 = \sum_{70} W_x \Longrightarrow 100 = \sum_{70} W_x/(1-p)\)
因此,在两种状态下经过网络层,得到的结果近似:
net = Net(input_num, d_prob=0.5)
net.linears[1].weight.detach().fill_(1.)
net.train() # 测试结束后调整回运行状态
y = net(x)
print("output in training mode", y)
net.eval() # 测试开始时使用
y = net(x)
print("output in eval mode", y)
output in training mode tensor([9942.], grad_fn=<ReluBackward1>)
output in eval mode tensor([10000.], grad_fn=<ReluBackward1>)
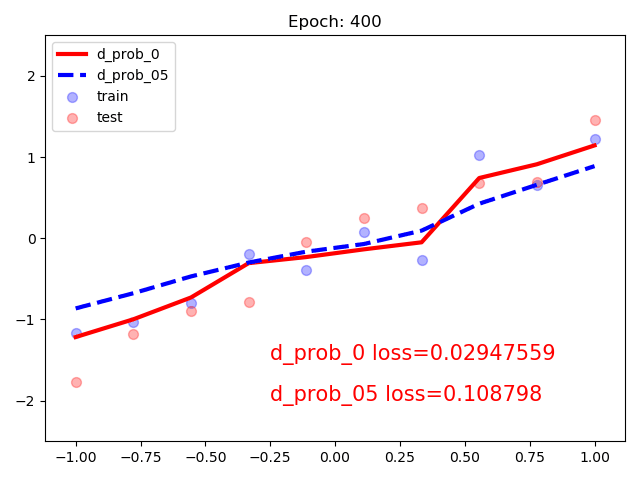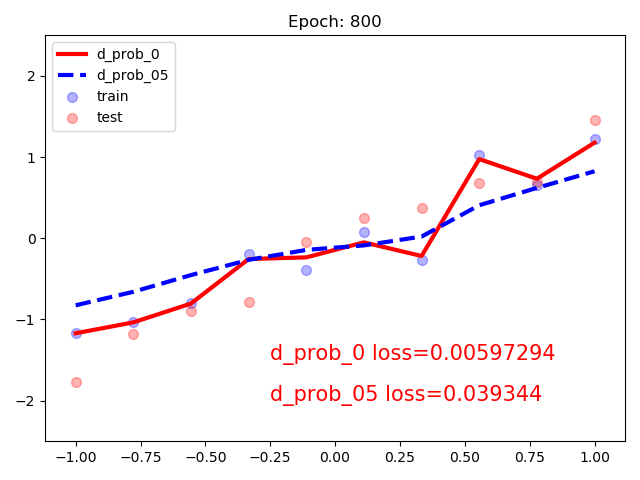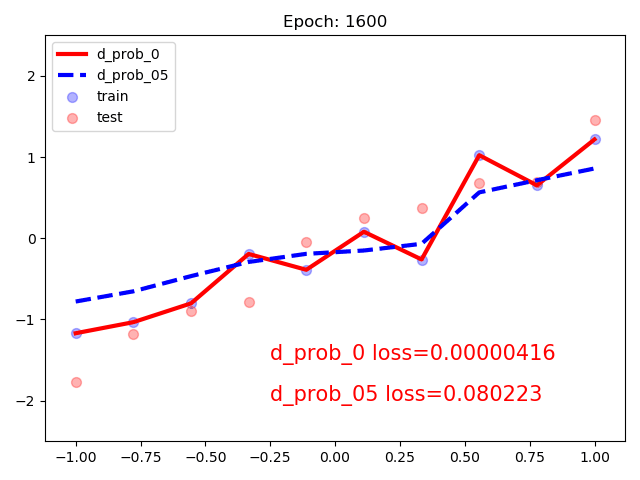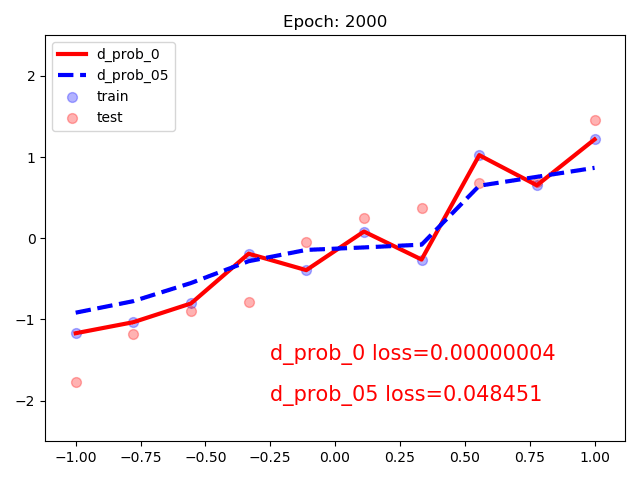
3. 仍以线性回归为例:
同时构建有dropout和没有的模型:随着训练次数增加,含有dropout的模型会更加平滑。
class MLP(nn.Module):
def __init__(self, neural_num, d_prob=0.5):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)
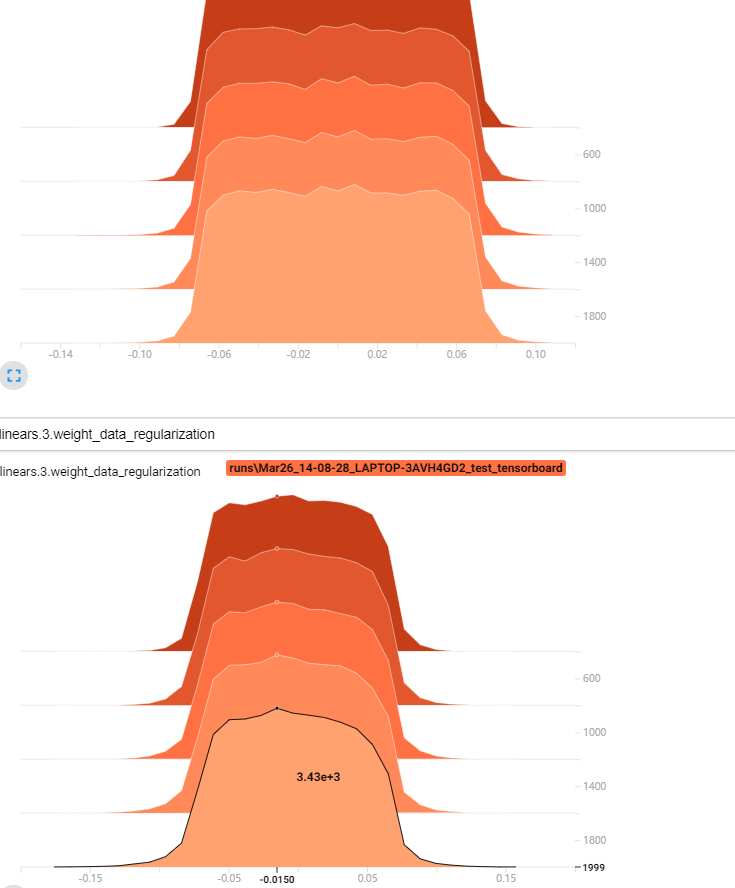
我们观察线性层的权重分布,可以明显看出来含有dropout的模型参数更集中,峰值更高
三、Batch Normalization
1. Batch Normalization:批标准化
批:一批数据,通常为mini-batch
标准化:0均值,1方差
优点:
- 可以用更大学习率,加速模型收敛
- 可以不用精心设计权值初始化
- 可以不用dropout或较小的dropout
- 可以不用L2或者较小的weight decay
- 可以不用LRN(local response normalization)

注意到,\(\gamma, \beta\)是可学习的参数,如果该层不想进行BN,最后学习出来\(\gamma = \sigma_{\Beta}, \beta = \mu_{\Beta}\),即恒等变换。
详见《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》阅读笔记与实现
2. Internal Covariate Shift (ICS)
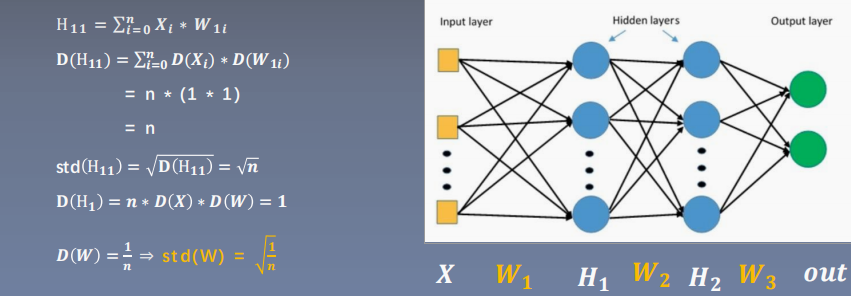
防止因为数据尺度/分布的不均使得梯度消失或爆炸,导致训练困难。
第四节提到的其他Normalization都是为了避免ICS.
3. _BatchNorm
pytorch中nn.BatchNorm1d nn.BatchNorm2d nn.BatchNorm3d 都继承于_BatchNorm,并且有以下参数:
__init__(self, num_features, # 一个样本特征数量(最重要)
eps=1e-5, # 分母修正项
momentum=0.1, # 指数加权平均估计当前mean/var
affine=True, # 是否需要affine transform
track_running_stats=True) # 是训练状态,还是测试状态
BatchNorm层主要参数:
- running_mean:均值
- running_var:方差
- weight:affine transform中的gamma
- bias: affine transform中的beta
训练:均值和方差采用指数加权平均计算
running_mean = (1 - momentum) * running_mean + momentum * mean_t
running_var = (1 - momentum) * running_var + momentum * var_t
测试:当前统计值
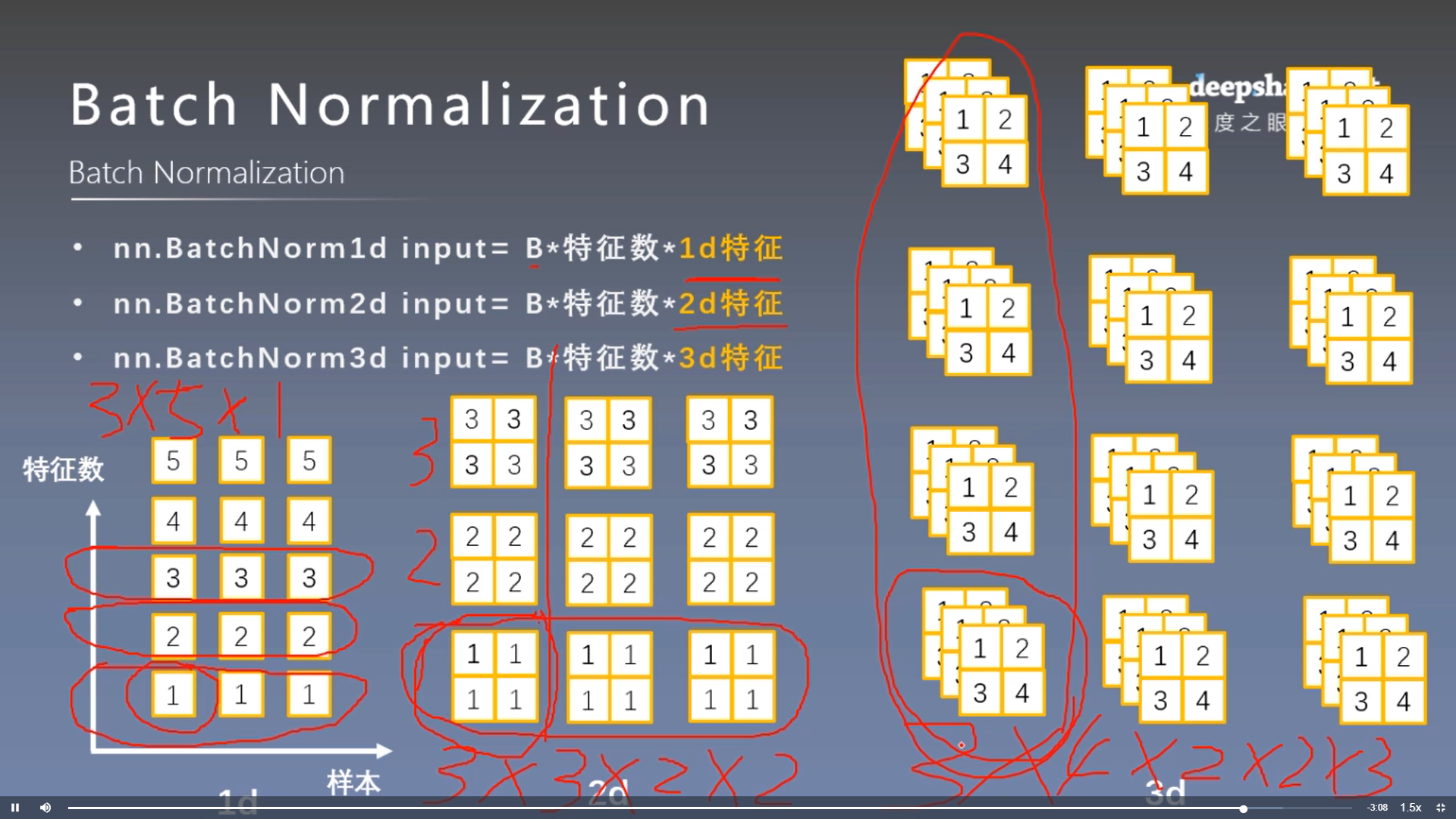
如上图所示:在1D,2D,3D中,特征数分别指 特征、特征图、特征核的数目。而BN是对于每个特征对应的所有样本求的均值和方差,故如上图中三种情况样本数分别为5,3,3,而对应的\(\gamma, \beta\)维数即5,3,3
4. 仍以人民币二分类为例:
我们原始的网络在卷积和线性层之后加入了BN层,注意其中卷积层后是2D BN,线性层后是1D
class LeNet_bn(nn.Module):
def __init__(self, classes):
super(LeNet_bn, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.bn1 = nn.BatchNorm2d(num_features=6)
self.conv2 = nn.Conv2d(6, 16, 5)
self.bn2 = nn.BatchNorm2d(num_features=16)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.bn3 = nn.BatchNorm1d(num_features=120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, classes)
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = F.relu(out)
out = F.max_pool2d(out, 2)
out = self.conv2(out)
out = self.bn2(out)
out = F.relu(out)
out = F.max_pool2d(out, 2)
out = out.view(out.size(0), -1)
out = self.fc1(out)
out = self.bn3(out)
out = F.relu(out)
out = F.relu(self.fc2(out))
out = self.fc3(out)
return out
def initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.xavier_normal_(m.weight.data)
if m.bias is not None:
m.bias.data.zero_()
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data, 0, 1)
m.bias.data.zero_()
- 使用
net = LeNet(classes=2)不经过初始化:
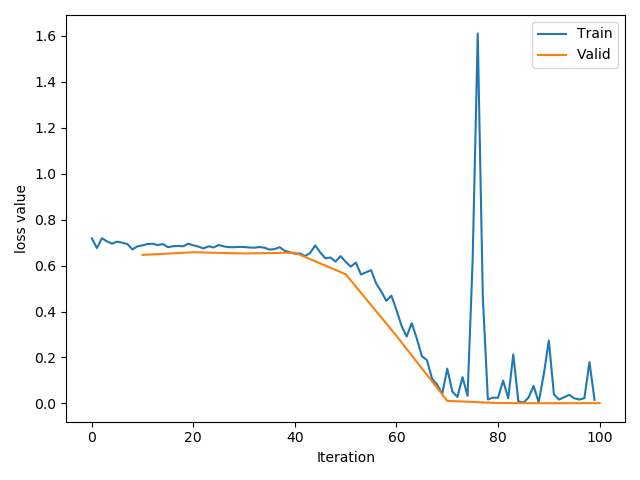
- 经过精心设计的初始化
net.initialize_weights():
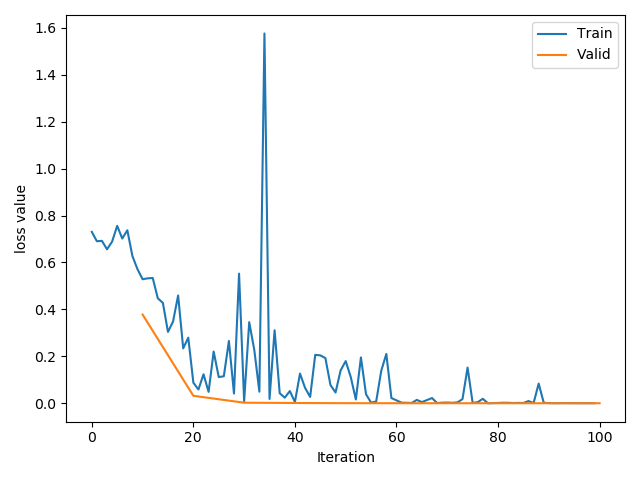
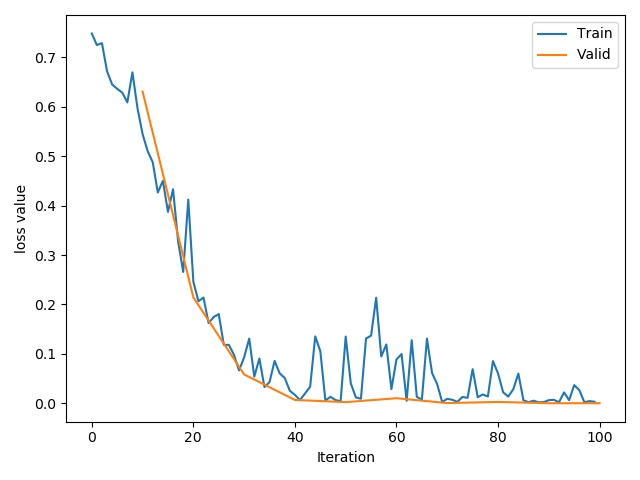
- 使用
net = LeNet_bn(classes=2)结果如下:即使Loss有不稳定的区间,其最大值不像前两种超过1.5
四、Normalizaiton_layers

1. Layer Normalization
起因:BN不适用于变长的网络,如RNN
思路:逐层计算均值和方差
注意事项:
- 不再有running_mean和running_var
- gamma和beta为逐元素的
nn.LayerNorm(normalized_shape, # 该层特征形状
eps=1e-05,
elementwise_affine=True # 是否需要affine transform
)
注意,这里的normalized_shape可以是输入后面任意维特征。比如[8, 6, 3, 4]为batch的输入,可以是[6,3,4], [3,4],[4],但不能是[6,3]
2. Instance Normalization
起因:BN在图像生成(Image Generation)中不适用,图像中输入的Batch各不相同,不能逐Batch标准化
思路:逐Instance(channel)计算均值和方差
nn.InstanceNorm2d(num_features,
eps=1e-05,
momentum=0.1,
affine=False,
track_running_stats=False)
# 同样还有1d, 3d

图像风格迁移就是一种不能BN的应用,输入的图片各不相同,只能逐通道求方差和均值
3. Group Normalization
起因:小batch样本中,BN估计的值不准
思路:数据不够,通道来凑
nn.GroupNorm(num_groups, # 分组个数,必须是num_channel的因子
num_channels,
eps=1e-05,
affine=True)
注意事项:
- 不再有running_mean和running_var
- gamma和beta为逐通道(channel)的
应用场景:大模型(小batch size)任务
当num_groups=num时,相当于LN
当num_groups=1时,相当于IN
4. 小结
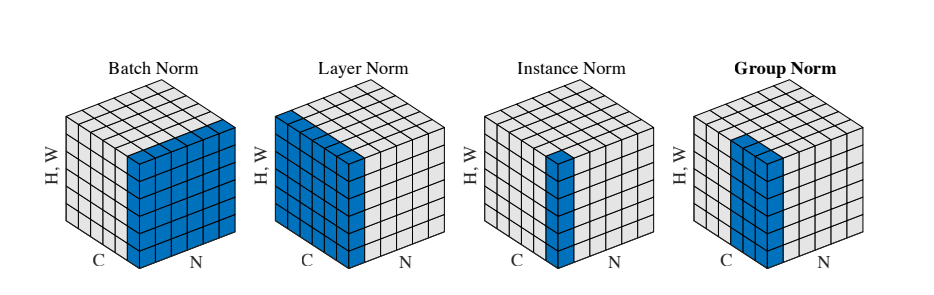
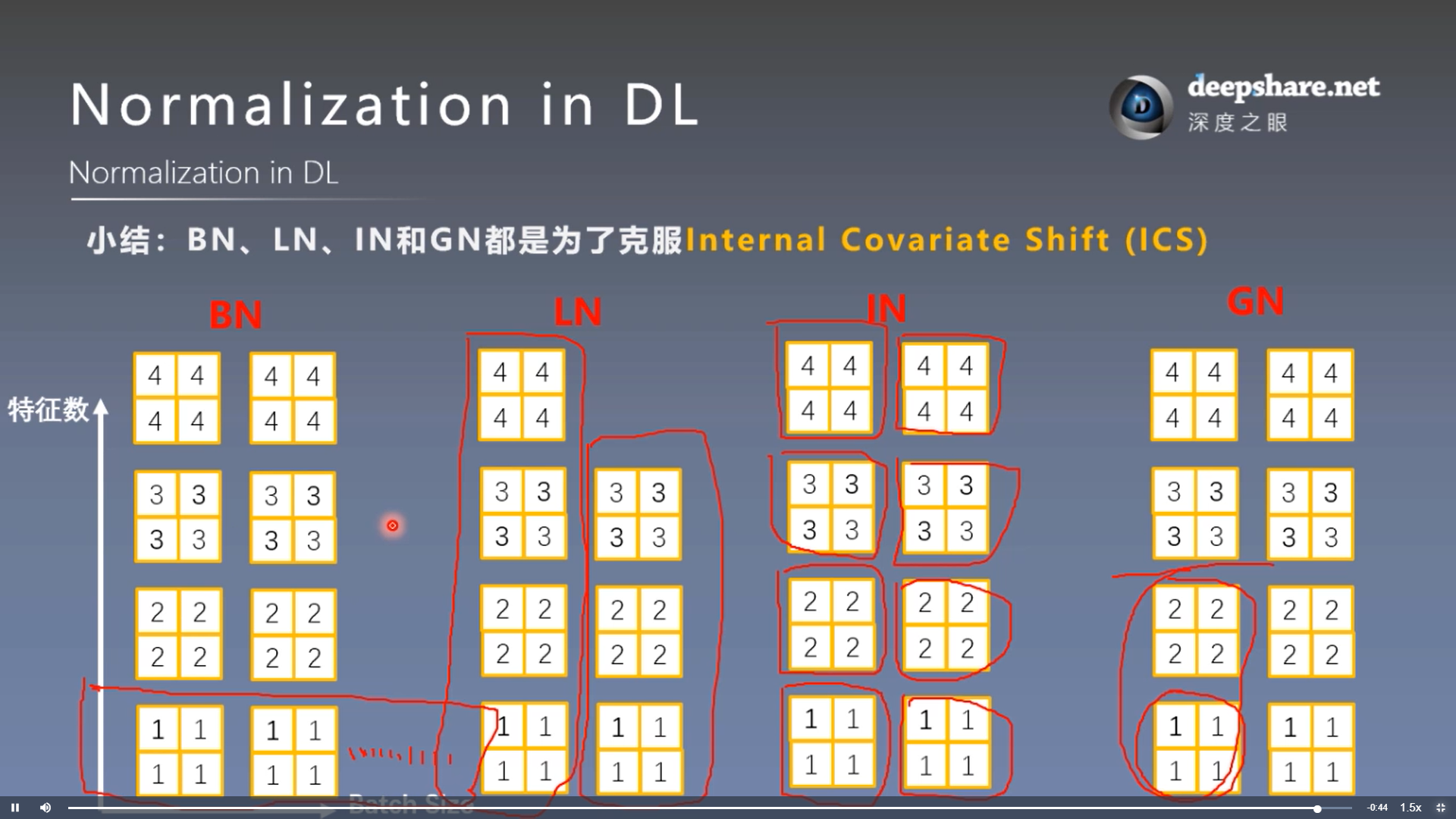
Pytorch_Part6_正则化的更多相关文章
- 数据预处理中归一化(Normalization)与损失函数中正则化(Regularization)解惑
背景:数据挖掘/机器学习中的术语较多,而且我的知识有限.之前一直疑惑正则这个概念.所以写了篇博文梳理下 摘要: 1.正则化(Regularization) 1.1 正则化的目的 1.2 正则化的L1范 ...
- 【原】关于使用sklearn进行数据预处理 —— 归一化/标准化/正则化
一.标准化(Z-Score),或者去除均值和方差缩放 公式为:(X-mean)/std 计算时对每个属性/每列分别进行. 将数据按期属性(按列进行)减去其均值,并处以其方差.得到的结果是,对于每个属 ...
- 正则化方法:L1和L2 regularization、数据集扩增、dropout
正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合).其直观的表现如下图所示,随着训练过程的进行,模型复杂度增加,在tr ...
- coursera机器学习-logistic回归,正则化
#对coursera上Andrew Ng老师开的机器学习课程的笔记和心得: #注:此笔记是我自己认为本节课里比较重要.难理解或容易忘记的内容并做了些补充,并非是课堂详细笔记和要点: #标记为<补 ...
- stanford coursera 机器学习编程作业 exercise 5(正则化线性回归及偏差和方差)
本文根据水库中蓄水标线(water level) 使用正则化的线性回归模型预 水流量(water flowing out of dam),然后 debug 学习算法 以及 讨论偏差和方差对 该线性回归 ...
- PRML读书会第五章 Neural Networks(神经网络、BP误差后向传播链式求导法则、正则化、卷积网络)
主讲人 网神 (新浪微博:@豆角茄子麻酱凉面) 网神(66707180) 18:55:06 那我们开始了啊,前面第3,4章讲了回归和分类问题,他们应用的主要限制是维度灾难问题.今天的第5章神经网络的内 ...
- 斯坦福第七课:正则化(Regularization)
7.1 过拟合的问题 7.2 代价函数 7.3 正则化线性回归 7.4 正则化的逻辑回归模型 7.1 过拟合的问题 如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集( ...
- 正则化,数据集扩增,Dropout
正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合).其直观的表现如下图所示,随着训练过程的进行,模型复杂度增加,在tr ...
- (五)用正则化(Regularization)来解决过拟合
1 过拟合 过拟合就是训练模型的过程中,模型过度拟合训练数据,而不能很好的泛化到测试数据集上.出现over-fitting的原因是多方面的: 1) 训练数据过少,数据量与数据噪声是成反比的,少量数据导 ...
随机推荐
- 攻防世界 reverse easy_Maze
easy_Maze 从题目可得知是简单的迷宫问题 int __cdecl main(int argc, const char **argv, const char **envp) { __int64 ...
- 【JVM进阶之路】七:垃圾收集器盘点
在前面,我们已经了解了JVM的分代收集,知道JVM垃圾收集在新生代主要采用标记-复制算法,在老年代主要采用标记-清除和标记-整理算法.接下来,我们看一看JDK默认虚拟机HotSpot的一些垃圾收集器的 ...
- istio sidecar使用自定义镜像源
Istio 和 sidecar 配置保存在 istio 和 istio-sidecar-injector 这两个 ConfigMap 中,其中包含了 Go template,所谓自动 sidecar ...
- Elasticsearch中最重要的文档CRUD要牢记
Elasticsearch文档CRUD要牢记 转载参考:https://juejin.im/post/5ddbf298e51d4523053c42e7 在Elasticsearch中,文档(docum ...
- " "( 双引号) 与 ' '( 单引号) 差在哪?-- Shell十三问<第四问>
" "( 双引号) 与 ' '( 单引号) 差在哪?-- Shell十三问<第四问> 经过前面两章的学习,应该很清楚当你在 shell prompt 后面敲打键盘.直到 ...
- 201871030122-牛建疆 实验三 结对项目——《D{0-1}KP 实例数据集算法实验平台》项目报告
项目 内容 课程班级博客链接 班级博客链接 作业要求链接 作业要求链接 我的课程学习目标 (1)体验软件项目开发中的两人合作,练习结对编程(Pair programming).(2)掌握Github协 ...
- 如何在 NET 程序万种死法中有效的生成 Dump (上)
一:背景 相信很多人都知道通过 任务管理器 抓取dump,虽然简单粗暴,但无法满足程序的无数种死法,比如: 内存膨胀,程序爆炸 CPU爆高,程序累死 应用无响应,用户气死 意外退出,和人生一样 既然手 ...
- Box UVA - 1587
Ivan works at a factory that produces heavy machinery. He has a simple job - he knocks up wooden box ...
- 编写shell脚本让springboot项目在CentOS中开机自启动
springboot项目部署在CentOS系统上时,如果遇到停电关机,公司的实施人员就得跑到甲方现场重新启动项目并测试,很是麻烦,这里探讨如何编写shell脚本控制springboot项目开机时自动启 ...
- Servlet与Netty横向对比
为什么要把这两个看起来不是很搭的东西放在一起对比呢?首先它们两个都是网络编程框架和规范,而且通过我的观察,从API的设计.生命周期方法.处理流程等等方面,他们确实有太多相似的地方了,如果想要深入地学习 ...
