【剑指Offer】07. 重建二叉树 解题报告（Java & Python & C++）

• 作者： 负雪明烛
• id： fuxuemingzhu
• 个人博客：http://fuxuemingzhu.cn/
• 个人微信公众号：负雪明烛

---

目录

• • 题目描述
  • 解题方法
  • • 基本方法：线性查找根节点的位置
    • 方法优化：使用 map 保存 inorder 中每个元素出现的位置
  • 日期

题目地址：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

• 0 <= 节点个数 <= 5000

解题方法

基本方法：线性查找根节点的位置

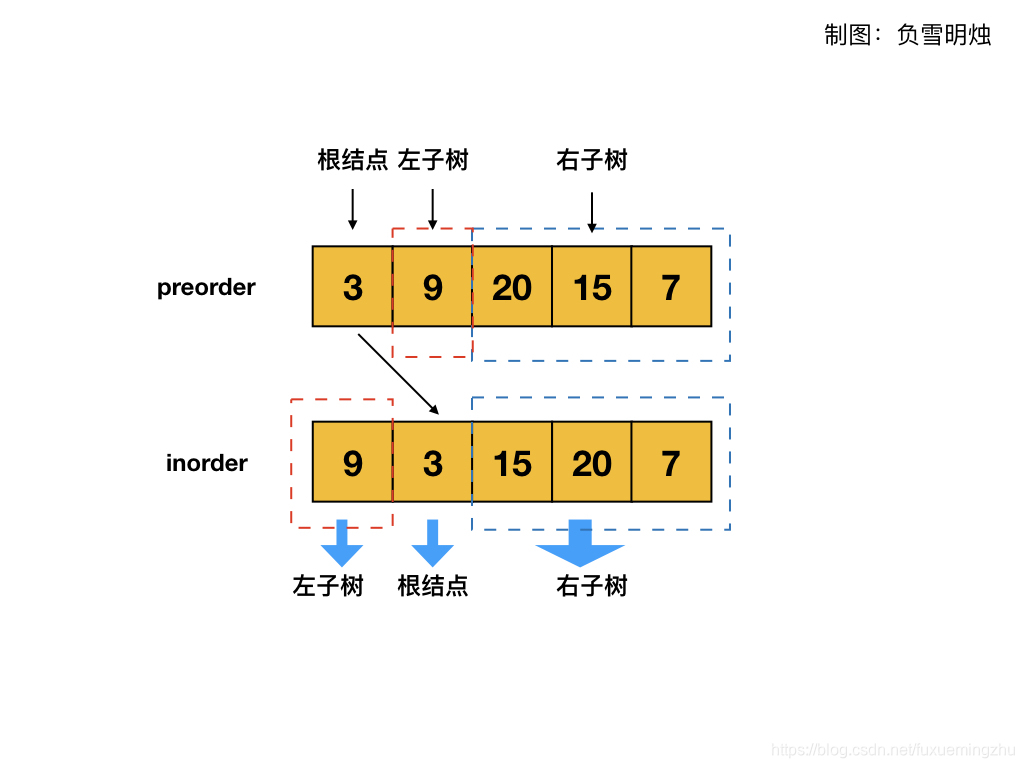
先看两种遍历方式的顺序：

• 前序遍历：根结点 -> 左子树 -> 右子树
• 中序遍历：左子树 -> 根结点 -> 右子树

我们看到前序遍历的第一个元素就是根结点，找到这个根结点在中序遍历种的位置，就能把中序遍历分为两部分：左子树和右子树。

然后根据中序遍历的左子树和右子树的元素的个数，就可以从前序遍历种区分出左右子树；

最后进行递归。

举个例子：

preorder = [3, 9, 20, 15, 7]
inorder = [9, 3, 15, 20, 7]

preorder 中的第一个元素是根结点，即 3。找出 3 在 inorder 中的位置，把inorder 分为左子树和右子树，长度分别是 1和3。也就确定了preorder 中的 [9]是左子树，[20,15,7] 是右子树。然后对左右子树进行递归即可。

java 代码如下：

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        return build(pre, in, 0, pre.length - 1, 0, in.length - 1);
    }
    public TreeNode build(int [] pre,int [] in, int s1, int e1, int s2, int e2){
        TreeNode node = new TreeNode(pre[s1]);
        int rootIndx = 0;
        for(int i = s2; i <= e2; i++){
            if(pre[s1] == in[i]){
                rootIndx = i;
                break;
            }
        }
        if(rootIndx != s2){
            node.left = build(pre, in, s1 + 1, s1 + (rootIndx - s2), s2, rootIndx - 1);
        }
        if(rootIndx != e2){
            node.right = build(pre, in, s1 + (rootIndx - s2) + 1, e1, rootIndx + 1, e2);
        }
        return node;
    }
}

Python 代码如下：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not preorder or not inorder: return None
        rootVal = preorder[0]
        rootPos = inorder.index(rootVal)
        root = TreeNode(rootVal)
        root.left = self.buildTree(preorder[1:1 + rootPos], inorder[:rootPos])
        root.right = self.buildTree(preorder[1 + rootPos:], inorder[rootPos + 1:])
        return root

方法优化：使用 map 保存 inorder 中每个元素出现的位置

我们在基本方法中看到一个可以优化的点：每次都从 inorder 中线性查找根节点，这步的时间复杂度是 O(N)。可以优化用一个全局的 map 保存 inorder 中每个节点和其位置的映射，这样查找根节点所在位置的是复杂度降到了 O(1)。

python 代码如下：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        self.posMap = { x : i for i, x in enumerate(inorder)}
        return self.build(preorder, inorder)

    def build(self, preorder, inorder):
        if not preorder or not inorder: return None
        rootVal = preorder[0]
        rootPos = self.posMap[rootVal]
        root = TreeNode(rootVal)
        root.left = self.buildTree(preorder[1:1 + rootPos], inorder[:rootPos])
        root.right = self.buildTree(preorder[1 + rootPos:], inorder[rootPos + 1:])
        return root

C++ 代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (preorder.empty() || inorder.empty())
            return nullptr;
        unordered_map<int, int> inorderPos;
        for (int i = 0; i < inorder.size(); ++i) {
            inorderPos[inorder[i]] = i;
        }
        return buildTreeOrder(preorder, inorder, inorderPos, 0, preorder.size() - 1, 0, preorder.size() - 1);
    }
    TreeNode* buildTreeOrder(vector<int>& preorder, vector<int>& inorder, unordered_map<int, int>& inorderPos, int preStart, int preEnd, int inStart, int inEnd) {
        if (preStart > preEnd || inStart > inEnd)
            return nullptr;
        int root_val = preorder[preStart];
        int inMid = inorderPos[root_val];
        TreeNode* root = new TreeNode(root_val);
        root->left = buildTreeOrder(preorder, inorder, inorderPos, preStart + 1, preStart + inMid - inStart, inStart, inMid - 1);
        root->right = buildTreeOrder(preorder, inorder, inorderPos, preStart + inMid - inStart + 1, preEnd, inMid + 1, inEnd);
        return root;
    }
};

日期

2017 年 4 月 20 日
2018 年 3 月 9 日
2021 年 8 月 5 日 —— 我离职了