[省选联考 2020 A 卷] 组合数问题

题意

[省选联考 2020 A 卷] 组合数问题

想法

自己在多项式和数论方面还是太差了，最近写这些题都没多少思路，看完题解才会

首先有这两个柿子

\(k*\dbinom{n}{k} = n*\dbinom{n - 1}{k - 1}\)

\((1 + x) ^ n = \sum_{i = 0}^{n}\dbinom{n}{i}x^i\)

然后对于题目中所要求的多项式\(f(x)\)我们自然把他拆开,对于一个单个\(k\)对答案贡献

\(\sum_{i = 1}^{m}a_i * (k^i * x^k * \dbinom{n}{k})\)

然后我们发现这个项\(k^i* \dbinom{n}{k}\)

是我们所给的第一个柿子的拓展

我们取\(i = 2\)来看看柿子的展开

\(k^2* \dbinom{n}{k}\)

\(k*((n) * \dbinom{n - 1}{k - 1})\)

\((k - 1 + 1)*((n) * \dbinom{n - 1}{k - 1})\)

\((k - 1)*n*\dbinom{n - 1}{k - 1} + n * \dbinom{n - 1}{k - 1}\)

\(n*(n - 1)*\dbinom{n - 2}{k - 2} + n * \dbinom{n - 1}{k - 1}\)

取\(i = 3.......\)

我们发现\(k^p * \dbinom{n}{k}\)

可以变为这个柿子

\(\sum_{i = 1}^pS(p,i)n^{\underline i}\dbinom{n - i}{k - i}\)

其中\(n^{\underline i}\)是下降幂

而\(S(p,i)\)这个系数可以这样推来\(S(p,i) = i * S(p - 1,i) + S(p - 1,i - 1)\)

当你在计算展开的时候我们注意到如果我们先把\(k\)给乘进去可以很自然的把一些柿子给转化成\(k^i-1\dbinom{n}{k}\)的展开形式

这个时候会给\(S(p,i)多一个S(p - 1,i - 1)的系数\)

然后我们会发现把可转化的柿子转化完后\(我们把k拆成(k - i + i)这个时候又会多一个i * S(p - 1,i)\)

这是一个好的结论

\(k^p * \dbinom{n}{k}\ =\ \sum_{i = 1}^pS(p,i)n^{\underline i}\dbinom{n - i}{k - i}\)

其中

\(S(p,i) = i * S(p - 1,i) + S(p - 1,i - 1)\)

然后我们往原柿子里带（打不动了）

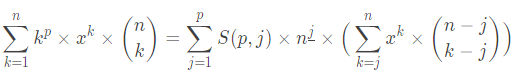
括号里用二项式定理打开

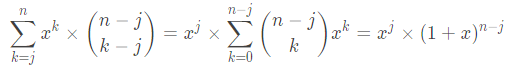
做完了

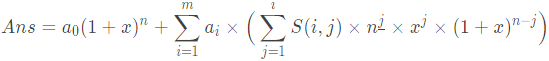
代码

#include <cstdio>
using namespace std;
typedef long long LL;
inline LL read()
{
	LL val = 0; char c = getchar();
	while(c < '0' || c > '9') c = getchar();
	while(c >= '0' && c <= '9') { val = val * 10 + (c ^ 48); c = getchar(); }
	return val;
}
const int M = 1005;
LL a[M], n, x, p, m, S[M][M], ans;
inline LL Qpow(LL b, LL c)
{
	LL res = 1;
	while(c)
	{
		if(c & 1) res = res * b % p;
		b = b * b % p;
		c >>= 1;
	}
	return res;
}
int main()
{
	n = read(); x = read(); p = read(); m = read();
	for(int i = 0; i <= m; i++) a[i] = read();
	S[1][1] = 1;
	for(int i = 2; i <= m; i++)
		for(int j = 1; j <= i; j++)
			S[i][j] = ((S[i - 1][j] * j) % p + S[i - 1][j - 1]) % p;
	ans = a[0] * Qpow(x + 1, n) % p;
	for(int i = 1; i <= m; i++)
	{
		LL sum = 0, tmp = n;
		for(int j = 1; j <= i; j++)
		{
			sum = (sum + (S[i][j] * tmp % p * Qpow(x, j) % p * Qpow(x + 1, n - j) % p)) % p;
			tmp = tmp * (n - j) % p;
		}
		ans = (ans + a[i] * sum % p) % p;
	}
	printf("%lld\n", ans);
	return 0;
}