洛谷 P5785 [SDOI2012] 任务安排

链接：

弱化版：P2365

题意：

有 $n$ 个任务待完成，每个任务有一个完成时间 $t_i$ 和费用系数 $f_i$，相邻的任务可以被分成一批。从零时刻开始这些任务会被机器分批完成，在每批任务开始前机器有一个给定启动时间 $s$，一批任务的完成时间是这批任务完成时间之和，同一批任务视作在同一时刻完成。

每个任务的费用是他的完成时刻和费用系数的乘积，请最小化总费用。

分析：

如果设 $dp[i]$ 为第 $i$ 个任务作为当前这一批任务的最后一个时的最优解，这样会很麻烦，因为会涉及到 "此时一共有多少批" 这个很麻烦的状态。这里有一个dp的trick：费用提前。

我们发现把第 $i$ 个任务作为当前这一批任务的最后一个时，当前批内以及后面的任务都会多一个 $s\cdot f_i$ 的费用，于是把 $dp[i]$ 改为第 $i$ 个任务作为当前这一批任务的最后一个时，加上后面任务的已有贡献的最优解。可以联系状态转移理解：

\[dp[i]=dp[j]+(\sum_{k=j+1}^if_i\times\sum_{k=1}^it_i)+s\sum_{k=j+1}^nf_i
\]

于是设 $sumf[i]=\sum\limits_{k=1}^if_k$，$sumt[i]=\sum\limits_{k=1}^it_k$

\[dp[i]=dp[j]+(sumf[i]-sumf[j])\times sumt[i]+s(sumf[n]-sumf[j])
\]

于是

\[dp[i]=dp[j]+sumf[i]sumt[i]-sumf[j]sumt[i]+s\cdot sumf[n]-s\cdot sumf[j]
\]

依套路：

\[(dp[j]-s\cdot sumf[j])=sumt[i]sumf[j]+(dp[i]-sumf[i]sumt[i]-s\cdot sumf[n])
\]

于是求斜率为 $sumt[i]$，过点 $(sumf[j],dp[j]-s\cdot sumf[j])$ 的直线的最小截距。

这里的 $sumt[i]$ 并不是单调的，所以不能用单调队列优化，一个优秀的办法是二分找到第一个与下一个点之间的斜率大于 $sumt[i]$ 的点，时间复杂度 $O(n\log n)$。

算法：

单调队列维护下凸包，然后每次二分找到最优决策点，根据其信息得到 $dp[i]$，继续维护凸包即可。时间复杂度 $O(n\log n)$。

重要的细节：

这道题让我注意到了一个斜率优化dp中的一个很重要的细节，就是维护下凸包的判断。

这道题在洛谷讨论区也有不少人曾发起过讨论，称因为精度问题而必须把判断斜率改成乘法，但其实并不是这样一个简单的借口，我们来看下面三个代码，他们除了维护下凸包的判断没有任何区别。

(Y(q[qt])-Y(q[qt-1]))*(X(i)-X(q[qt])) >= (Y(i)-Y(q[qt]))*(X(q[qt])-X(q[qt-1])) 100pts

slope(q[qt],q[qt-1])>=slope(i,q[qt]) 80pts

slope(q[qt],q[qt-1])>=slope(i,q[qt-1]) 100pts

显然，这并不是精度的问题，甚至这三种写法都是错的！

我们来看下面这种情况：（这种情况虽然在数据上比较难构造，但单纯考虑维护下凸包来看还是很常见的）

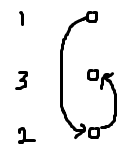
这样三个横坐标相等点从上到下按 $1,3,2$ 的次序被加入下凸包的维护。

显然，根据人脑判断，这样的数据要维护下凸包自然是保留 $2$ 号点，弹出 $3$ 号点，但普遍的写法是不存在 "弹出当前点" 这种操作的，只有 "弹出上一个点"。于是：

如果是第一种判断，两边的乘积都是 $0$，于是会弹出 $2$ 号点，此时 $1,3$ 点间斜率为 -inf，后面的点可以加入，但在局部确实出现了正确性的错误。

如果是第二种判断，由于 $1,2$ 间斜率是 -inf，$2,3$ 点间斜率是 +inf，所以不会有点弹出，此时 $2,3$ 点之间斜率为 +inf，这种情况下，后面的点根本无法加入下凸包的维护了，出现了严重的问题。

如果是第三种判断，由于 $1,2$ 间斜率是 -inf，$1,3$ 点间斜率是 -inf，这里也涉及取等的问题，如果取等，那么会弹出 $2$ 号点，变成第一种情况；如果不取等，那么 $2$ 号点不会被弹出，于是变成第二种情况。

所以这题错误的真正原因根本不是什么精度，而是维护下凸包的做法在存在横坐标相等的情况下本来就是假的！

根据这题横坐标非严格单调增，一个感觉比较正确的做法是在维护下凸包时先判断与前面的点横坐标是否相等，如果相等，保留纵坐标最低的点；如果不等，按照原本的做法即可。

在这样的做法下，不等号是否取等是没有正确性的影响的。取等会弹出一些无用的点，可能会快几毫秒。

所以在有横坐标相等的情况下，一个正确的写法是：

if(X(i)==X(q[qt])&&1<qt){if(Y(i)<Y(q[qt]))qt--;else continue;}

while(1<qt&&slope(q[qt],q[qt-1])>=slope(i,q[qt]))qt--;

q[++qt]=i;

这样写的话，不管判断是用的乘法还是斜率，哪两个斜率判断，或者取不取等，都是能过的。不排除真的会有精度错误，但我认为不能把根据观察发现除法比乘法劣的情况统一归咎到精度错误上。

代码：

#include<bits/stdc++.h>

using namespace std;

#define int long long

#define in read()

inline int read(){

	int p=0,f=1;

	char c=getchar();

	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}

	while(isdigit(c)){p=p*10+c-'0';c=getchar();}

	return p*f;

}

#define X(x) (sumf[x])

#define Y(x) (dp[x]-sumf[x]*s)

#define dx(x,y) (X(x)-X(y))

#define dy(x,y) (Y(x)-Y(y))

#define slope(x,y) ((double)dy(x,y)/dx(x,y))

const int N=3e5+5;

const int inf=0x7fffffffffffffff;

int n,s,t[N],f[N],sumt[N],sumf[N],dp[N],q[N],qt;

inline int bin(int key){

	int l=1,r=qt,mid;

	while(l<r){

		mid=(l+r)>>1;

		double cp=(mid==qt)?inf:slope(q[mid+1],q[mid]);

		if(cp<key)l=mid+1;

		else r=mid;

	}

	return l;

}

signed main(){

	n=in,s=in;

	for(int i=1;i<=n;i++)

		t[i]=in,f[i]=in,

		sumt[i]=sumt[i-1]+t[i],

		sumf[i]=sumf[i-1]+f[i];

	qt=1;

	for(int i=1;i<=n;i++){

		int qh=bin(sumt[i]);

		dp[i]=Y(q[qh])-sumt[i]*X(q[qh])+sumf[i]*sumt[i]+sumf[n]*s;

		if(X(i)==X(q[qt])&&1<qt){if(Y(i)<Y(q[qt]))qt--;else continue;}

		while(1<qt&&slope(q[qt],q[qt-1])>slope(i,q[qt-1]))qt--;

		q[++qt]=i;

	}

	cout<<dp[n];

	return 0;

}

题外话：

这个重要的细节确实让我对斜优里维护下凸包部分的印象深了许多。