230th Weekly Leetcode Contest

题目二

题目描述

5690. 最接近目标价格的甜点成本  难度：中等-中等

题解

解法一：三进制状态压缩

　　考虑到baseCosts、toppingCosts的长度最多都为10，每一种辅料都有加0、1、2份的选择，因此可以考虑三进制状态压缩求解。类似二进制的状态压缩。

以10种辅料为例。

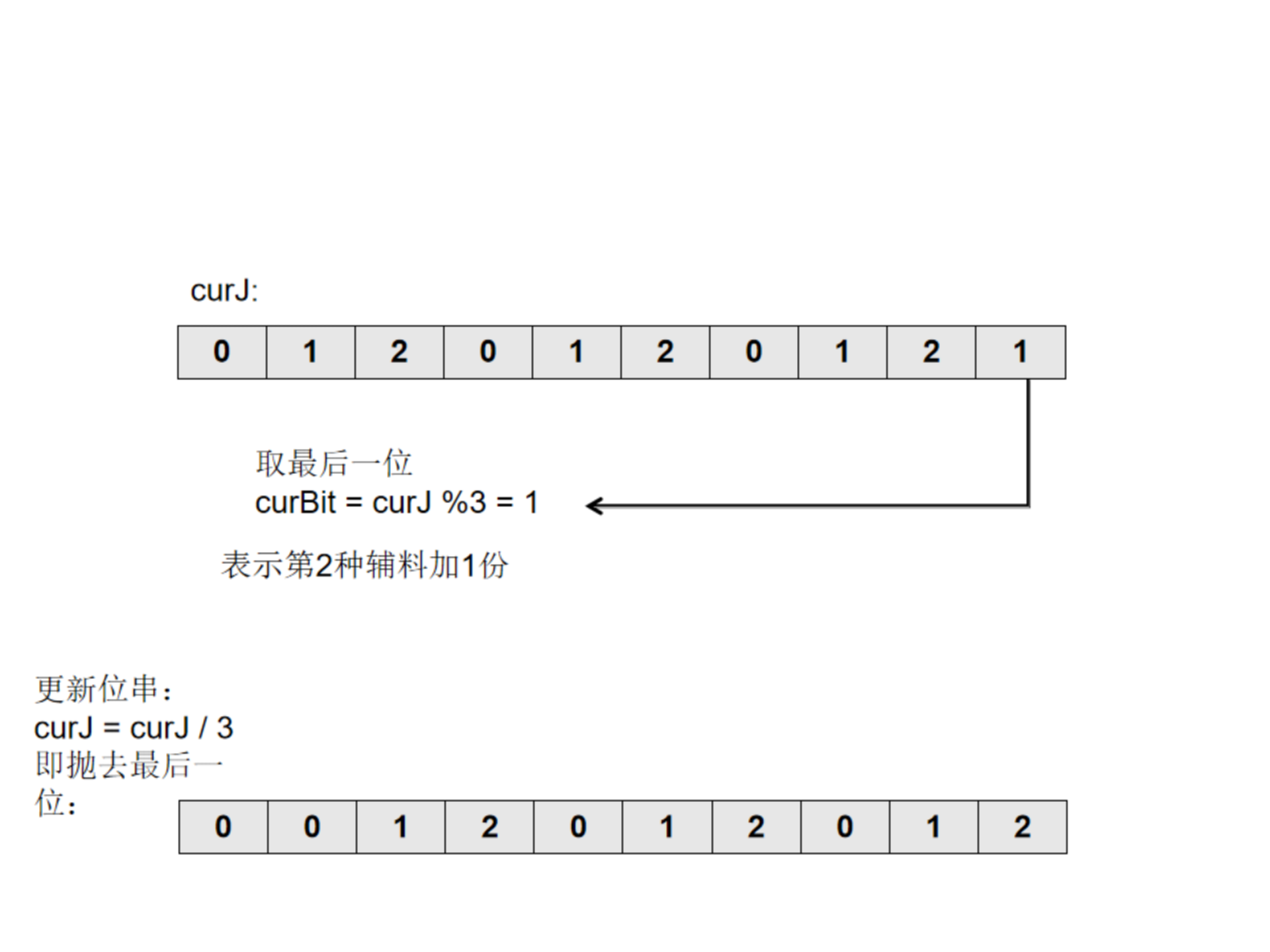
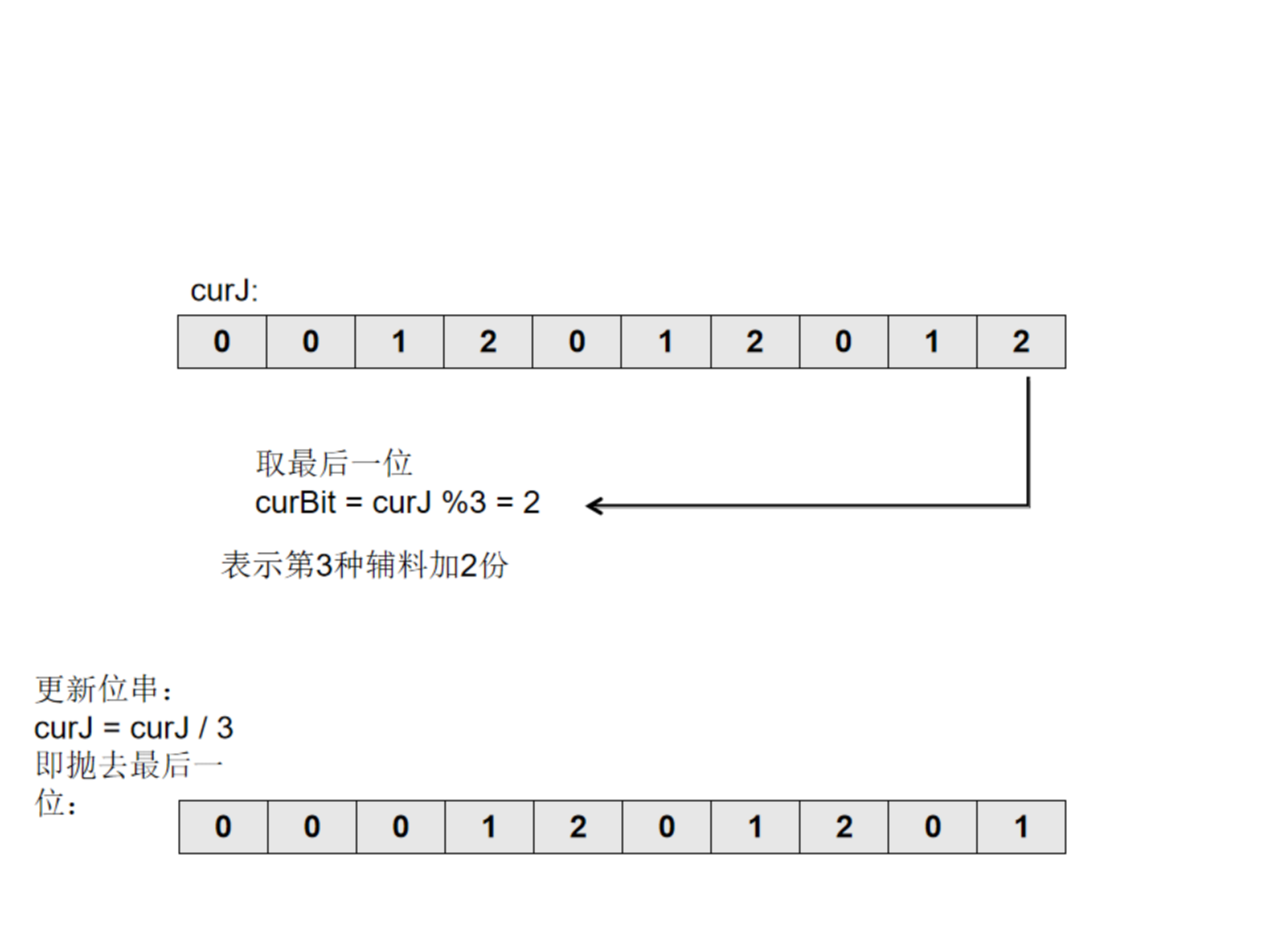
直到curJ为0。

代码：

 1 class Solution {
 2     public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
 3         Arrays.sort(baseCosts);
 4         Arrays.sort(toppingCosts);
 5         int nearestCost=0;//记录最接近的成本
 6         int minGap = Integer.MAX_VALUE;//记录目前最接近的成本和目标成本target的差
 7         for(int i=0;i<baseCosts.length;i++){//每一种基料
 8             for(int j=0;j<Math.pow(3,toppingCosts.length);j++){//三进制位串
 9                 int cost = baseCosts[i];
10                 int curJ = j;//现在的位串
11                 int index = 0;
12                 while(curJ!=0){//取位串的每一位
13                     int curBit = curJ % 3;//位串的当前一位
14                     curJ /= 3;
15                     cost += toppingCosts[index]*curBit;
16                     index++;
17                 }
18                 if(Math.abs(cost-target)==0){//若现在的成本恰好是target，直接返回
19                     return target;
20                 }else if(Math.abs(cost-target)<minGap){//若目前的成本更接近target，更新nearestCost和minGap;
21                     minGap = Math.abs(cost-target);
22                     nearestCost = cost;
23                 }else if(Math.abs(cost-target)==minGap){//若目前的成本和已经找到的最接近成本与目标成本的差距相等，取成本较小者（题目要求）
24                     if(cost<nearestCost){
25                         nearestCost = cost;
26                     }
27                 }
28             }
29         }
30         return nearestCost;
31     }
32 }

略微优化代码：

　　当目前的cost>target 且 Math.abs(cost-target)>minGap时，由于cost随着位串的遍历单调不减，这种方案可以不再考虑，肯定不优于已经求得的成本，因此可以剪枝。

　　

 1 class Solution {
 2     public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
 3         Arrays.sort(baseCosts);
 4         Arrays.sort(toppingCosts);
 5         int nearestCost=Integer.MAX_VALUE;//记录最接近的成本
 6         int minGap = Integer.MAX_VALUE;//记录目前最接近的成本和目标成本target的差
 7         for(int i=0;i<baseCosts.length;i++){//每一种基料
 8             for(int j=0;j<Math.pow(3,toppingCosts.length);j++){//三进制位串
 9                 int cost = baseCosts[i];
10                 int curJ = j;//现在的位串
11                 int index = 0;
12                 boolean isCut = false;
13                 while(curJ!=0){//取位串的每一位
14                     int curBit = curJ % 3;//位串的当前一位
15                     curJ /= 3;
16                     cost += toppingCosts[index]*curBit;
17                     index++;
18                     if(cost>target&&Math.abs(cost-target)>minGap){//剪枝
19                         isCut = true;
20                         break;
21                     }
22                 }
23                 if(isCut==true){//剪枝
24                     continue;
25                 }
26                 if(Math.abs(cost-target)==0){//若现在的成本恰好是target，直接返回
27                     return target;
28                 }else if(Math.abs(cost-target)<minGap){//若目前的成本更接近target，更新nearestCost和minGap;
29                     minGap = Math.abs(cost-target);
30                     nearestCost = cost;
31                 }else if(Math.abs(cost-target)==minGap){//若目前的成本和已经找到的最接近成本与目标成本的差距相等，取成本较小者（题目要求）
32                     if(cost<nearestCost){
33                         nearestCost = cost;
34                     }
35                 }
36             }
37         }
38         return nearestCost;
39     }
40 }

解法二：动态规划

本题数据范围很小，暴力枚举辅料组合就可以通过，但时间复杂度为指数级。

把问题转化为背包问题，可以将时间复杂度降低到多项式级别。

• 因为每种辅料最多可以用两次，所以直接把每种辅料变成两个。
• 基料必须且只能选一种，可以首先处理好。

题目三

题目描述

5691. 通过最少操作次数使数组的和相等 难度：中等-中等

题解-贪心法

看到题目后，总结出以下要点：

• 总和大的数组中元素减小等同于总和小的数组中元素增大（这样转化后，我们在求得每个数组的总和后，两个总和不再狭义地代表每个数组的总和）
• 要实现最小操作次数，考虑从最小的元素开始增大，增大到最大，如1直接变成6；或从最大的元素开始减小，减小到最小，如6直接变成1。
• 如何判断是否已经满足条件呢？既然我们是保证每次改变量都是最大，那么，如果这次改变后，最好是两个总和相等，那么功德圆满，即使不相等，但若实现了两个总和的反转（即大小关系反转），那么因为我们是最大的改变量，我们只需在心中将这次的改变量减小一点，如原来是2直接到6，我们可以改变2到5、4等等，肯定能实现两个总和的相等。
• 题目中固定1-6的数据范围，我们可以指定一个大小为6的数组inc[] (为了方便,inc[0]不用),inc[1]代表两个数组中1或6的个数（总和大的数组中的1可以增大到6、总和小的数组中的6可以减小到1），inc[2]代表两个数组中2或5的个数（总和大的数组中的2可以增大到6、总和小的数组中的5可以减小到1）

 1 class Solution {
 2     public int minOperations(int[] nums1, int[] nums2) {
 3         if(Math.min(nums1.length,nums2.length)*6<Math.max(nums1.length,nums2.length)*1){
 4             return -1;
 5         }
 6         int nums1Sum = 0;
 7         int nums2Sum = 0;
 8         for(int i=0;i<nums1.length;i++){//统计nums1的和
 9             nums1Sum += nums1[i];
10         }
11         for(int i=0;i<nums2.length;i++){//统计nums2的和
12             nums2Sum += nums2[i];
13         }
14         if(nums1Sum==nums2Sum){
15             return 0;
16         }
17         int[] inc = new int[6];//统计nums1 和 nums2中可以增大或减小的数的个数，即1 ~ 5的个数；为了方便，数组容量多1，inc[0]不用
18         if(nums1Sum<nums2Sum){
19             for(int i=0;i<nums1.length;i++){//nums1Sum较小，考虑nums1中可以增大的数
20                 if(nums1[i]<6){ // 1 ~ 5
21                     inc[nums1[i]]++;
22                 }
23             }
24             for(int i=0;i<nums2.length;i++){//nums2Sum较大，考虑nums2中可以减小的数
25                 if(nums2[i]>1){ // 2 ~ 6    nums2减小相当于nums1增大,如6减小到1，同1增加到6t；又如5减小到1同2增加到6
26                     inc[7-nums2[i]]++;
27                 }
28             }
29             int cnt=0;
30             for(int i=1;i<=5;i++){//此后的nums1Sum已经不是真正意义上的nums1的和
31                 while(inc[i]!=0){
32                     nums1Sum += 6 - i;
33                     inc[i]--;
34                     cnt++;
35                     if(nums1Sum>=nums2Sum){
36                         return cnt;
37                     }
38                 }
39             }
40         }else if(nums1Sum>nums2Sum){
41             for(int i=0;i<nums2.length;i++){//nums2Sum较小，考虑nums2中可以增大的数
42                 if(nums2[i]<6){ // 1 ~ 5
43                     inc[nums2[i]]++;
44                 }
45             }
46             for(int i=0;i<nums1.length;i++){//nums1Sum较大，考虑nums1中可以减小的数
47                 if(nums1[i]>1){ // 2 ~ 6    nums1减小相当于nums2增大,如6减小到1，同1增加到6；又如5减小到1同2增加到6
48                     inc[7-nums1[i]]++;
49                 }
50             }
51             int cnt=0;
52             for(int i=1;i<=5;i++){
53                 while(inc[i]!=0){
54                     nums2Sum += 6 - i;
55                     inc[i]--;
56                     cnt++;
57                     if(nums2Sum>=nums1Sum){
58                         return cnt;
59                     }
60                 }
61             }
62         }
63          return -1;
64     }
65 }

题目三

题目描述

5691. 通过最少操作次数使数组的和相等  难度：困难-简单

题解