OO_Unit1_表达式求导总结

OO的第一单元主要是围绕表达式求导这一问题布置了3个子任务，并在程序的鲁棒性与模型的复杂度上逐渐升级，从而帮助我们更好地提升面向对象的编程能力。事实也证明，通过这3个task的练习，我的OO水平也在各方面得到了不同程度的提高，包括但不限于模型的设计、对Java中各类容器的使用和重载以及测试手段的多样化等等。接下来我将分别就这3个task对我的代码进行分析，同时总结自己的一些收获与心得。

Task 1

任务目标：实现由简单幂函数构成的多项式的求导

任务特点：

保证输入格式的绝对正确（对程序的鲁棒性没有要求）
多项式仅由幂函数和其系数构成，不存在纵向与横向的深度拓展

代码结构度量

Task1的代码UML图如下：

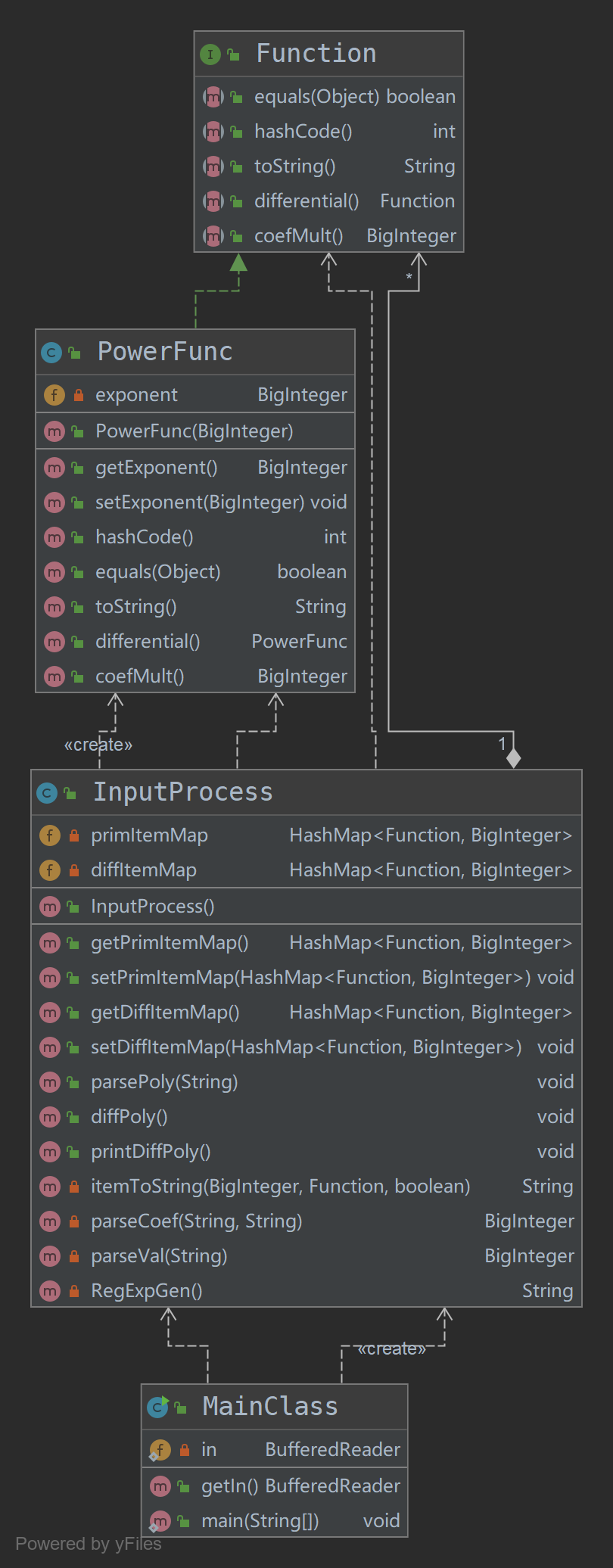
可以看到，在task1中，面向过程的思想依然十分明显，绝大部分的处理都是在InputProcess类中完成，PowerFunc主要是充当了一种数据单元作用。之所以如此，我认为原因有二：

Task1的任务本身比较简单，没有太多需要处理的对象，也就没有进行建模的必要
自己在设计本次任务的模型时，仍然是从过程的角度出发，即按照输入处理——求导——输出的思路进行编程，这在本质上还是一种面向过程的思维方式。

但同时，为了尽可能向后兼容，我在此时就已经设计了一个Function接口，试图将幂函数中的一些共性方法抽离出来，为后面的任务中可能出现的增加新的函数这样的横向拓展做好准备。

代码复杂度分析

Task1的各类代码复杂度如下表所示。

Class Name	NOF	NOM	NOPM	LOC	WMC	DIT(E)	LCOM
Function	0	5	0	7	5	0	-1
InputProcess	2	12	8	148	31	0	0.416667
MainClass	1	2	2	20	2	0	0
PowerFunc	1	8	8	50	13	1	0

可以看到，正如上文所言，InputProcess类的长度和加权方法数都明显高于其他类，这正是面向过程的编程思想所导致的结果。

测试分析

Task1的难度相对较低，主要是为了让同学们能够更好地适应全新的Java编程环境，虽然之前有了pre的铺垫，但作为正式OO作业的第一篇章，Task1的难度低一些也在情理之中。因此，我的程序在测试中并未出现什么bug，但是我在互测环节却仍然发现了其他同学的3个非同质bug，在此列举如下：

当出现两个连续的 '-' 时，求导的结果就会出现问题
由于使用了大正则匹配导致的极端数据下的栈溢出
对于对空格的处理不当（没有直接去掉空格），结果莫名使得项前面的符号在处理的过程中被丢弃了。

这三个bug都给我本人以一定程度的启发，第2个bug提高了我对于压力测试的重视；第3个bug则直接导致了我更加坚定了先把空格字符丢弃掉的决心，但这却在一定程度上为task2中的bug埋下了伏笔。

Task 2

任务目标：实现对由幂函数、正余弦函数构成的表达式的求导

任务特点：

鲁棒性方面，增加了非合法空白字符引起的格式错误的检测与判断
模型复杂度方面，增加了正余弦函数，并允许表达式中的项由多个函数构成，这相当于对Task1进行了横向拓展

代码结构度量

Task2的代码UML图如下：

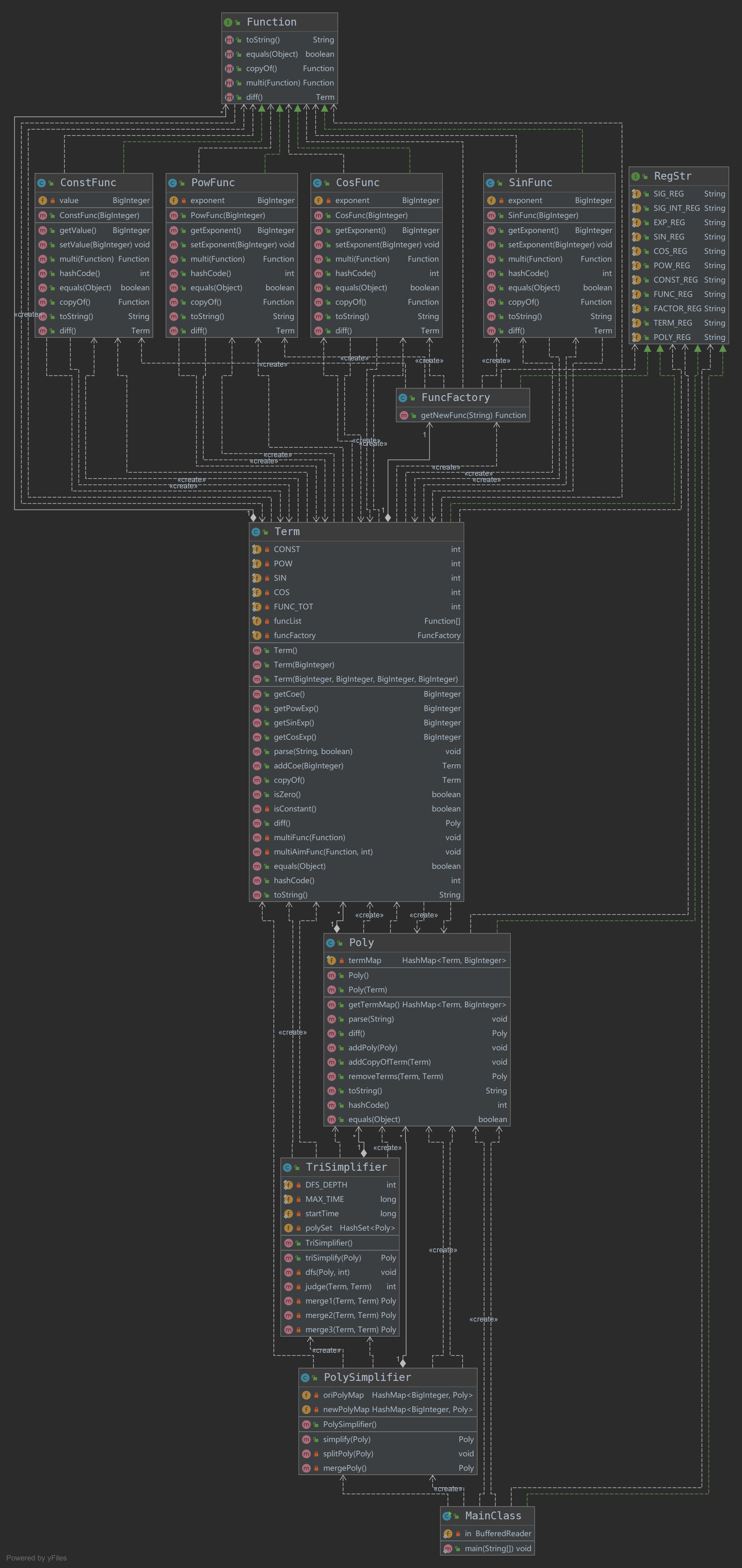
Task2的整体架构相比于Task1在复杂度上已经有了相当大程度的提升，也为task3打下了一个很好的基础。通过Poly-->Term-->Function这样的一个结构，我成功地将输入的多项式进行了拆解；同时由于函数种类的增加，我引入了FuncFactory类也就是工厂模式来构造不同的函数，以达到降低耦合度的目的。总体来看，Task2中值得强调的主要是以下两点：

Task2中的解析表达式字符串还是完全利用正则来实现，这是与Task1一以贯之的。这里我们通过RegStr接口将所有的正则表达式封装在一起，可以极大地降低debug的难度，便于进行统一的管理。
在优化方面，Task2采用完全构造单独的优化类来对生成的多项式进行优化，也就是将优化的部分与求导等其他模块完全解耦，从而降低复杂度。具体而言，这里的优化主要是三角函数的优化，这里我们利用记忆化搜索，通过，，这三个最基本的三角公式对原多项式进行递归遍历，寻找所有的化简结果中最短的一项，最终的结果可以说是相当完美了。至于时间控制，则是利用限制递归深度+设置熔断时间来防止出现TLE的现象。

代码复杂度分析

Task2中各类的代码复杂度如下表所示：

Class Name	NOF	NOM	NOPM	LOC	WMC	DIT(E)	LCOM
ConstFunc	1	9	9	43	12	1	0.222222
CosFunc	1	9	9	51	14	1	0
FuncFactory	0	1	1	31	7	0	-1
Function	0	5	0	7	5	0	-1
MainClass	1	1	1	34	2	0	0
Poly	1	11	11	117	32	0	0.272727
PolySimplifier	2	4	2	42	8	0	0
PowFunc	1	9	9	54	15	1	0
RegStr	11	0	0	13	0	0	-1
SinFunc	1	9	9	51	14	1	0
Term	7	18	15	175	45	0	0
TriSimplifier	4	7	2	100	20	0	0.714286

可以看到，总体而言Task2在耦合度的控制上做的还算差强人意。即便在横向进行了扩展，增加了优化方法，但由于在设计中将这些都完全地独立了出去，因此客观上限制了各个类的复杂度。

测试分析

说来惭愧，自己在task2中的强测和互测中都出现了一个bug（而且都是很蠢的那种）：

强测里的Bug是自己在处理空白字符时把'\t'写成了'\s'，结果把所有的空白字符都去掉了，导致合法性判断出现纰漏
互测里的Bug是自己在处理指数的绝对值范围时直接用正则进行判定，即要么是4位数，要么刚好为10000，结果忘掉了前导0的存在。然后由于自己把所有的RegStr都写在一起了，结果被有心人一眼就看出来了...

这两个bug暴露出的问题是：

在本地自测的时候只考虑了正确性测试，忘记了进行全面的鲁棒性测试，导致在空白符的处理上出现问题；
由于自己在本地测试的时候也是用的同样的正则生成的测试数据，所以默认就是没有前导0的，结果第二个bug自己也没发现
程序写的明明白白只有两个下场：自己若足够完美自然会让大家只读不hack，否则只会死的明明白白。

但仔细一想，这真的是测试不到位的问题吗？或许是的，但我同时觉得这是因为自己在一开始进行架构设计的时候就对这两个细节没有做到足够敏感，潜意识里压根就不重视。所以我更觉得这是一个审题的问题，get到客户需求真的是一切的前提的前提啊。

此外，自己在互测中也发现了一些其他同学的bug，总结如下：

指数绝对值刚好等于10000被判为WF（边界条件）
莫名地就是求导不对
类似2中的求导运算错误……

嗯，不过这个架构在性能上的表现还是很不错滴~

Task 3

任务目标：在Task2的基础上，实现可以嵌套的表达式的求导：具体的嵌套包括：项层面允许因子为多项式，函数层面允许三角函数的底数为因子。

任务特点：

相比于Task2，鲁棒性上增加了对于空白字符位置的合法性检测
同时通过允许嵌套，增加了任务的纵向深度，使得难度有所上升。

代码结构度量

Task3的代码UML图如下...

可以看到，Task3里的代码结构一下子就变得扑朔迷离了起来……嗯，但这其实是无法避免的，因为考虑到Poly, Term, Factor之间存在许多的相互调用关系（解析、求导、化简、输出），所以就使得类与类之间存在很深的依赖。总体而言，Task3在保留了Task2的工厂方法外，还通过继承HashMap的方式实现了一个自定义容器类VarItemSet以便更好地合并同类项。

此外，在化简方面，这里分成了两种化简方式，一种是基于模型的内部化简，即根据对象本身的属性特征判断其可否进行转化（如项变成表达式，表达式变成普通因子等等），从而尽可能减少递归深度；另一种是基于公式法则的外部化简，即根据一些简单的运算法则，如将形如这样的表达式因子进行展开等。之所以这样做，是因为前者的化简很自然，并且必然存在事实上的最优解；而后者则不一定存在算法上的最优解，因此需要对化简进行额外的限制和处理以防TLE。

代码复杂度分析

Task3中各类的代码复杂度如下表所示：

Class Name	NOF	NOM	NOPM	LOC	WMC	DIT(E)	LCOM
ConstFactor	1	10	10	45	13	1	0.2
CosFactor	2	9	9	82	19	1	0.222222
Factor	0	3	0	5	3	0	-1
FactorFactory	6	8	1	180	38	0	1
Main	1	2	2	34	5	0	1
Poly	1	17	16	207	52	1	0.117647
PolySimplifier	1	5	2	54	12	0	0.6
PowFactor	1	9	9	53	14	1	0.444444
PreParser	0	3	1	77	17	0	-1
SinFactor	2	9	9	82	19	1	0
Term	4	25	18	333	85	1	0.08
VarItem	0	2	0	4	2	0	-1
VarItemSet	0	4	4	26	7	0	-1

在Task3中，Term类作为承上启下至关重要的一环，承担的任务也比较艰巨，因此在复杂度上远超其他类（Poly紧随其后）。除此之外，其他类还算是分布的比较均匀。总体而言，Task3的耦合度与复杂度应该是3次任务中最高的(Task2最低)，我认为这里面最主要的原因就是存在类之间的循环调用，但我觉得这似乎没办法避免？无论圈画的再大（比如单独设置一个表达式因子类做一个缓冲），还是终究要回到原点。

仅就架构层面而言，我认为Task3中最具争议的一点就是是否需要把化简方法完全地剥离出来，我的架构里给出的答案是否定的，我认为这样更加自然，但这不可避免地增加了类的复杂度。那么如果从“高内聚，低耦合”的基本设计原则来看呢，把化简方法全部放到外面可能也不符合“低耦合”的原则：因此综上，我认为我目前采用的这种架构设计算是在耦合度与复杂度之间的一个比较好的折衷。

测试分析

Task3里，由于自己在本地进行了更加全面多样的测试，包括压力测试，边界测试等等，以及个人感觉强测数据略弱的缘故，所以强测中没有出现bug。但是在互测中，厉害的roommates还是给我上了一课，找到了我的程序中的两个非同质bug，具体如下：

进行多项式外部化简的时候，我调用了一个multiCoe()方法，这个方法是用来乘常数系数的，并且返回一个新的多项式，然而我忘了自己的所有multi开头的方法都是返回新的对象（所有以add开头的方法都是改变原有对象），结果就没有取它的返回值，也就是调用了相当于没有调用，结果就gg了。
进行内部化简的时候，自己对于表达式因子向一般因子转换的判定中忽略了表达式不含项的情况(如(x-x))，结果在输出的时候出现了一点异常。

这两个bug我觉得应该是由于程序复杂性增加后的必然，不是说避免不了的必然，而是说必须要通过测试才有可能de出来的必然。~~（没错，这是一个概率学问题）~~也就是自己的测试仍然还不够到位的原因。

对于bug1，我想最有效的测试方法应该是单元测试，即每完成一个小的单元就进行针对性测试，这样可以只需要少量测试数据就可以做到全面，考虑到日后程序整体上将变得越来越复杂，单元测试必不可少。此外，单元测试对于新增功能也特别有帮助，这就很好地避免了今天写的代码第二天调用的时候就忘了它具体是要干嘛的尴尬局面。

而对于bug2，我认为这是自己在构造测试数据时还不够仔细全面的缘故，自己只考虑了cos(0)的情况，却没考虑cos((0))的情况，正所谓你以为你一共就1层，而你的roommates却给你挖出了第2层。所以啊，下次一定要自己把所有的层都挖出来才行。

当然，在互测中，自己也发现其他同学的两个非同质bug，列举如下：

嵌套层数过多时，出现TLE的情况
括号间空格引起的WF错误

写在最后——我对Unit1的一点思考

Thinking 1.1 设计模式的应用

整个表达式单元的设计模型如下：

由于就整体上来看，模型中的每一项既是组成最后的“产品”中的一环，也同时承担了“生产下一级产品”的任务，因此难以将其进一步分解成更多的对象。从过程的角度来看，或许可以把化简乃至其他的部分抽离出来单独作为一个工具类（也就是“加工车间”）来使用，但具体是否需要这样做，我认为还是取决于化简方法本身的复杂度是否到了非给它单独一个类（特殊待遇）的程度。

因此，这里我仅仅是应用了工厂模式将构造不同形式的因子从Term中分离了出来，这主要是因为因子层面的种类较多而导致的。在今后的任务中是否有必要应用其他的设计模式，咱们就具体问题具体分析好了。

Thinking 1.2 关于本地评测

本地评测我是利用python中的sympy，Xeger和subprocess模块搭建的评测机，尚未使用单元测试，这个评测机我感觉在测试上对我的帮助没有达到我预期的效果，这应该是因为我给它的自由度太高，导致随机的范围太大，以致于对于诸多的极端情况表现得并不如我自己手动构造一些测试用例来的效果更好。

因此，我认为后面如果还有必要本地搭建评测机的话，应该尽量将测试点分的更加细致，从纵向和横向两个角度对问题进行分解，针对所有的组合情况进行测试~~（这不就是手造数据吗）~~；此外还需要特别注意压力测试与边界测试的情况，确保在极端数据下程序仍然能够正常运行。

对于互测部分，这里我采用的策略同样是定向爆破+大规模随机数据相结合的方式，简单来说就是凡是我自己之前发现的bug我都会拿来测别人，此外评测机会不会随机发现一些新的bug就不好说了这样。但是神奇的是，在实际进行互测的时候，我发现大家的bug似乎并不重合，也就是我出bug的地方似乎大家都没问题，我认为很显然不用测试的地方却神奇地发现了别人的bug...

究其原因，我觉得首先应该是不同人的架构设计不同，因此容易出现bug，或者说逻辑比较复杂的部分也不相同：比如有同学可能会把解析作为一种预处理，那他这一块的复杂度就比较高，也就容易出Bug；但如果是逐层进行解析，那么每一层的复杂度都会较低，也就不容易出现问题了。此外，还可能是因为大家在测试的时候构造样例的侧重点不一样，因为如前所述，普通的评测机只能测试一些比较一般的情况，极端数据需要自己手造，但可能大家考虑的点不一样，所以测试的时候忽略的部分也就不同了。

基于此，我认为后面除了进一步优化评测机以外呢，最好还要把不同的测试数据与不同的架构之间联系起来。也就是思考大家可能的架构都有哪些，不同的架构可能出现问题的地方都有哪些，这样才进行测试或许针对性会更好。

Thinking 1.3 性能与向后兼容

最后我想说的一点是关于性能与兼容性之间的矛盾。这里并不是说为了做到向后兼容就必须要牺牲性能，或者为了性能就难以向后兼容。而是说在相同规模的程序复杂度的前提下，性能与向后兼容是无法做到绝对的同时兼顾的。以表达式求导问题为例，Task2中的基于三角公式的化简就很难套用到Task3上，但是Task2本身的性能可以说是优化得相当不错了。究其原因，我认为是因为在模型的复杂度本身提高的情况下，将其与原复杂度条件下的性能优化同等看待本身就是不合理的。因为这里我们需要首先使得新模型的复杂度降到原模型的层面，然后才能套用原模型的方法对其进行优化，而前一步本身就需要额外的程序复杂度的开销。换而言之，这其中显然存在着某种类似于“时间换空间，空间换时间”般的守恒关系。无论多么优秀的程序员，在同等条件下，都无法跨越这条天然的鸿沟——除非将其直接填平。