noip模拟42

A. 卷

发现乘积足以爆 \(long\) \(long\)，但是数据随机，可以略忽略精度问题

一个快速降低数的级别的方法是取对数，由于有性质 \(log(x * y)=logx+logy\)，合并时运算会很方便，于是转化成加和型最大独立集问题

---

B. 简单题

观察发现对于每个奇数，其 \(2\) 倍放在另一个集合，\(4\) 倍放在当前集合，以此类推

那么对于一条偶数长度的链，一定一半放在第一个集合，另一半放在第二个集合，对答案贡献乘 \(2\)

对于奇数长度的链，一定分成 \(len\) 和 \(len+1\) 两部分，那么这样最终答案一定有可行区间 \([l,r]\)，那么多出 \(l\) 的部分一定是若干个奇数链造成的，而奇数链又是自由组合，设总数为 \(tot\)，答案为 \(\binom{tot}{m-l}\)

发现组合数数过大，模数很小，可以用 \(lucas\) 定理计算

对于计算奇偶链的个数，考虑枚举链长，这是 \(log\) 级别的，那么长度的 \(k\) 的链的起点范围为 \(\displaystyle[\frac{n}{2^{k-1}}+1,\frac{n}{2^k}]\)，因为这个不分奇数，得除以 \(2\)

代码实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=5005;
const int maxm=11000025;
const int mod=10000019;
int n,q,x,tot1,tot2,l,r,frac[maxm],inv[maxm],ans,ans1,len;
int po(int a,int b=mod-2){
	int ans=1;
	while(b){
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return ans;
}
int read(){
	int x=0,f=1;
	char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=x*10+ch-48;
		ch=getchar();
	}
	return x*f;
}
void pre(){
	frac[0]=1;
	for(int i=1;i<=mod-1;i++)frac[i]=frac[i-1]*i%mod;//,cout<<frac[i]<<" ";
	inv[mod-1]=po(frac[mod-1]);
//	cout<<frac[mod]<<" "<<inv[mod]<<endl;
	for(int i=mod-2;i>=0;i--)inv[i]=(i+1)*inv[i+1]%mod;//,cout<<inv[i]<<" ";
	return ;
}
int C(int n,int m){
	if(n<m)return 0;
	if(n==m)return 1;
	return frac[n]*inv[m]%mod*inv[n-m]%mod;
}
int lucas(int x,int y){
//	cout<<"hhh "<<x<<" "<<y<<endl;
	if(x==y)return 1;
	if(x<y)return 0;
	if(x<mod&&y<mod)return C(x,y);
	return lucas(x/mod,y/mod)*C(x%mod,y%mod)%mod;
}
signed main(){
//	cout<<po(2);
	n=read();
	q=read();
	pre();
//	cout<<C(6,2)<<endl;
	len=log2(n)+1;
//	cout<<len<<endl;
	for(int i=1;i<=len;i++){
//		cout<<i<<endl;
		int po1=pow(2,i-1);
		int po2=pow(2,i);
		int up=n/po1;
		int down=n/po2+1;
		if(down&1)down--;
		if(up&1)up++;
		int num=(up-down)/2;
		if(i&1){
			tot1+=num;
		}
		else tot2+=num;
		l+=num*(i/2);
	}

	r=l+tot1;
//	cout<<tot1<<" "<<tot2<<" "<<l<<" "<<r<<endl;
	ans1=po(2,tot2);
//	cout<<"ppp "<<endl;
	for(int i=1;i<=q;i++){
		x=read();
		if(x<l||x>r){
			puts("0");
			continue;
		}
		ans=ans1*lucas(tot1,x-l)%mod;
		printf("%d\n",ans);
	}
	return 0;
}

---

C. 粉丝

这道题本质是自然数拆分，运用根号分治优化

首先自然数拆分有两种 \(dp\) 方法：

设 \(f[i][j]\) 表示 \(dp\) 到 \(i\) 这个数和为 \(j\) 的方案数，\(f[i][j]=f[i-1][j]+f[i][j-i]\)

\(g[i][j]\) 表示分成了 \(i\) 个数字，和为 \(j\) 的方案数

发现两种 \(dp\) 单独做都是 \(n^2\) 的

但是观察第一种 \(dp\) 的状态是 \(dp\) 到 \(i\) 这个数，值域越小复杂度越低

第二种状态是分成 \(i\) 个数，值域越大复杂度越低

于是在 \(\sqrt n\) 处分治，值域小的部分用第一种，大的部分用第二种，总复杂度为 \(n\sqrt n\)

注意第二种 \(dp\) 其实是每个选了了的数都已经以 \(sq\) 为基准了，那么实际的总和需要加上 \(num*sq\)，这个合并时用 \(num\) 记录

代码实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e5+5;
int x,y,n,mod,f[maxn],g[maxn],sum[maxn],sq,ans;
int dp(int limit){
	memset(f,0,sizeof f);
	memset(g,0,sizeof g);
	memset(sum,0,sizeof sum);
	ans=0;
	f[0]=1;
	sq=max((int)sqrt(n),limit);
	for(int i=limit;i<sq;i++){
		for(int j=i;j<=n;j++){
			f[j]+=f[j-i];
			f[j]%=mod;
		}
	}
	g[0]=1;
	sum[0]=1;
	for(int i=1;i<=n/sq;i++){
		int t=i*sq;
		for(int j=i;j+t<=n;j++){
			g[j]=(g[j]+g[j-i])%mod;
		}
		for(int j=0;j+t<=n;j++){
			sum[j+t]+=g[j];
			sum[j+t]%=mod;
		}
	}
	for(int i=0;i<=n;i++){
		ans=(ans+f[i]*sum[n-i]%mod)%mod;
	}
	return ans;
}
signed main(){
	cin>>x>>y>>n>>mod;
	cout<<(dp(x)-dp(y+1)+mod)%mod;
	return 0;
}

---

D. 字符串

首先可以把两端本身就对称的部分砍掉，作为 \(A\) 和 \(E\) 的部分，然后中间找一个回文串进行扩展

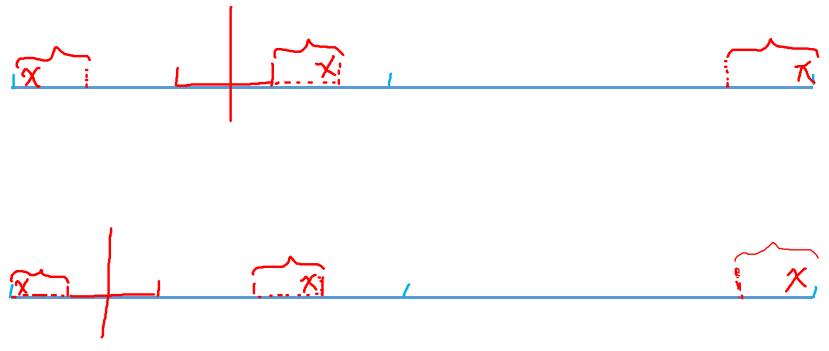
会出现一下两种情况

那么找相同串的情况可以翻转一次接在最后做一遍 \(KMP\)，由于中间插入了一个特殊字符，\(KMP\) 后不会跨边界

代码实现

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e7+5;
char c[maxn],a[maxn],b[maxn];
int n,cnt1,tot,len,cnt,p[maxn],ans,nxt[maxn],mx[maxn];
void manacher(){
	memset(p,0,sizeof p);
	for(int t=1,mid=0,r=0;t<=cnt;t++){
		if(t<=r)p[t]=min(p[mid*2-t],r-t+1);
		while(a[t+p[t]]==a[t-p[t]])p[t]++;
		if(t+p[t]>r)r=p[t]+t-1,mid=t;
	}
	return ;
}
void init(){
	for(int i=1;i<=len/2;i++){
		if(c[i]==c[len-i+1])tot++;
		else break;
	}
	n=len-tot*2;
	for(int i=1;i<=n;i++){
		c[i]=c[i+tot];
	}
	return ;
}
void pre(){
	a[0]='?';
	a[cnt=1]='#';
	for(int i=1;i<=n;i++){
		a[++cnt]=c[i];
		a[++cnt]='#';
	}
}
void kmp(){
	memset(nxt,0,sizeof nxt);
	memset(mx,0,sizeof mx);
	for(int i=cnt1-1,j=0;i>=1;i--){
		while(j&&b[i]!=b[cnt1-j])j=nxt[j];
		if(b[i]==b[cnt1-j])j++;
		nxt[i]=j;
	}
	for(int i=n;i>=1;i--){
		mx[i]=max(mx[i+1],nxt[i]);
	}
	return ;
}
void pre1(){
	cnt1=n;
	for(int i=1;i<=n;i++)b[i]=c[i];
	b[++cnt1]='$';
	for(int i=n;i>=1;i--){
		b[++cnt1]=c[i];
	}
	return ;
}
void solve(){
	for(int i=1;i<=cnt;i++){
		int posl=(i-p[i])/2;
		int posr=(i+p[i])/2;
		if(nxt[posr]<=posl)ans=max(ans,p[i]-1+nxt[posr]*2);
		if(mx[posr]>=posl)ans=max(ans,p[i]-1+posl*2);
	}
	return ;
}
void work(){
	pre();
	manacher();
	pre1();
	kmp();
	solve();
	return ;
}
int main(){
	scanf("%s",c+1);
	len=strlen(c+1);
	init();
	if(tot==n/2){
		cout<<n;
		return 0;
	}
	work();
	reverse(c+1,c+n+1);
	work();
	cout<<ans+tot*2;
	return 0;
}