M-SOLUTIONS Programming Contest 2021(AtCoder Beginner Contest 232) 题解

目录

• G - Modulo Shortest Path
• H - King's Tour

因为偷懒就只写G和H的题解了。

G - Modulo Shortest Path

首先可以观察到对于一条从点\(i\)到点\(j\)的边，权值只有两种：\(A_i+B_j\)和\(A_i+B_j-M\)。

那么我们假如把点按照\(B\)升序排成一列，那么当中的一个点肯定只会向前半部分连权值为\(A_i+B_j\)的边，后半部分连权值\(A_i+B_j-M\)的边。

我们可以把一个点拆成入点和出点（此时仍旧按照\(B\)升序排成两列），由出点向入点连权值为\(A_i+B_j\)和\(A_i+B_j-M\)的这两种边，入点向对应出点连接权值为\(0\)的边。

虽然此时边数仍旧是\(O(N^2)\)的，但是我们可以在每一个入点向下一个入点连一条权值为它们的\(B_i\)的差值的边，可以看成是一种反悔操作，走到入点了可以不走向出点，而是往下一个入点继续走，再走到对应的出点。这样发现没有必要给每一个点的出点连那么多条边出去了，只需要两条，一条连向序列开头的点，一条连向第一个使得权值和大于等于\(M\)的点。那么每一条原来的出点向入点连接的边都可以看成是一条现在出点向入点连接的边和一条入点构成的链的组合。

接下来只需要从起点到终点跑最短路就行了。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int n,m,S,T;
pair<pair<int,int>,int> a[200005];
vector<pair<int,int>> g[400005];
ll d[400005];

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i].first.first;
    for(int i=1;i<=n;i++)cin>>a[i].first.second,a[i].second=i;
    sort(a+1,a+1+n,[](const pair<pair<int,int>,int> &a,const pair<pair<int,int>,int> &b){
        if(a.first.second!=b.first.second)return a.first.second<b.first.second;
        return a.second<b.second;
    });
    S=1;
    while(a[S].second!=1)S++;
    T=1;
    while(a[T].second!=n)T++;
    for(int i=1;i<n;i++){
        g[n+i].emplace_back(n+i+1,a[i+1].first.second-a[i].first.second);
    }
    for(int i=1;i<=n;i++){
        g[n+i].emplace_back(i,0);
        g[i].emplace_back(n+1,a[i].first.first+a[1].first.second);
        int l=1,r=n,mid,res=-1;
        while(l<=r){
            mid=l+r>>1;
            if(a[i].first.first+a[mid].first.second>=m){
                res=mid;
                r=mid-1;
            }else{
                l=mid+1;
            }
        }
        if(res!=-1)g[i].emplace_back(n+res,a[i].first.first+a[res].first.second-m);
    }
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q;
    q.emplace(0,S);
    memset(d,0x3f,sizeof(d));
    d[S]=0;
    while(!q.empty()){
        ll cd;
        int x;
        tie(cd,x)=q.top();
        q.pop();
        if(cd>d[x])continue;
        for(auto &[y,z]:g[x])if(d[y]>cd+z){
            q.emplace(d[y]=cd+z,y);
        }
    }
    cout<<d[T]<<'\n';

    return 0;
}

H - King's Tour

比赛时没有想到递归处理的我真是铸币呜呜呜

首先可以考虑只有两行或者只有两列的棋盘怎么处理，那么由于八向移动的特性可以这么处理（起点在左上角，红点为终点）：

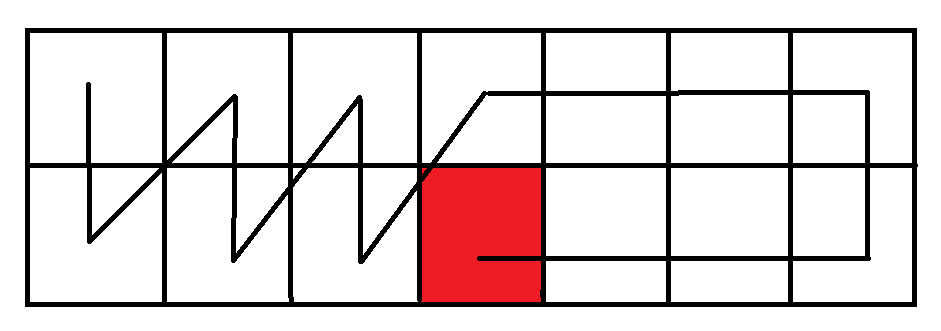
然后就考虑行数和列数都至少为\(3\)的情况（同样默认起点左上角），尝试走过最上方的一行，或者最左边的一列，由于终点一定不会在左上角，且行数和列数都大于\(2\)，那么一定两种操作可以选做一种，并且做完以后剩下来没访问过的棋盘仍旧是满足起点在一个角上且终点不和起点相同位置。

然后递归处理即可。

#include<bits/stdc++.h>
using namespace std;

vector<pair<int,int>> sol(int n,int m,int a,int b){
    vector<pair<int,int>> r;
    if(m==2){
        for(int i=1;i<a;i++){
            r.emplace_back(i,1);
            r.emplace_back(i,2);
        }
        for(int i=a;i<=n;i++)r.emplace_back(i,b^3);
        for(int i=n;i>=a;i--)r.emplace_back(i,b);
    }else if(n>2&&(a>2||a==2&&b!=m)){
        for(int i=1;i<=m;i++)r.emplace_back(1,i);
        for(auto &[x,y]:sol(n-1,m,a-1,m+1-b))r.emplace_back(x+1,m+1-y);
    }else{
        r=sol(m,n,b,a);
        for(auto &[x,y]:r)swap(x,y);
    }
    return r;
}

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n,m,a,b;
    cin>>n>>m>>a>>b;
    for(auto &[x,y]:sol(n,m,a,b))cout<<x<<' '<<y<<'\n';

    return 0;
}