例行检查我就不放了，64位的程序放入ida中

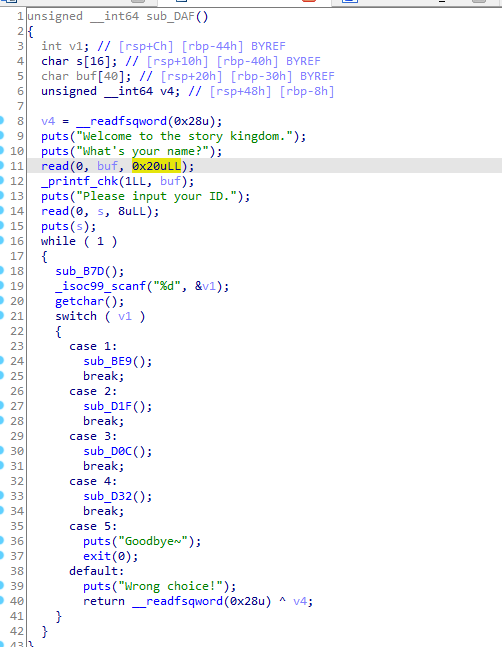
可以看到s到buf的距离是0x10，因为puts是遇到\x00截止。而且题目没有限制我们s输入的数量，所以可以通过这个puts泄露出libc的基值

很明显的uaf漏洞，因为该题的libc版本是2.27所以可以通过double free来做这道题，比较简单

完整exp如下

成功获取到flag

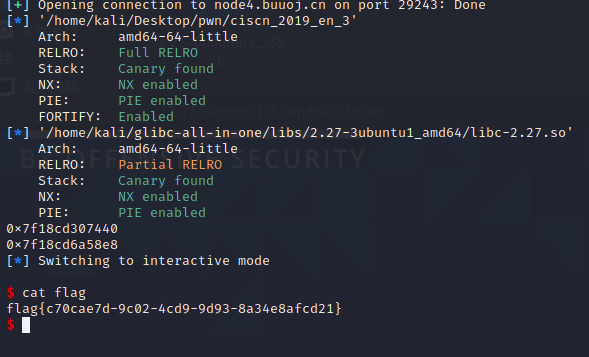
结束！！！！

ciscn_2019_en_3的更多相关文章

随机推荐

  1. Vue3学习与实战 · 全局挂载使用Axios

    在vue2中会习惯性的把axios挂载到全局,以方便在各个组件或页面中使用this.$http请求接口.但是在vue3中取消了Vue.prototype,在全局挂载方法和属性时,需要使用官方提供的gl ...

  2. Kubernetes Deployment 最佳实践

    零.示例 首先给出一个 Deployment+HPA+ PodDisruptionBudget 的完整 demo,后面再详细介绍其中的每一个部分: apiVersion: apps/v1 kind: ...

  3. MYSQL免安装

    MYSQL免安装 本文使用mysql 8.0.22进行演示 一.MYSQL 下载 [x] 官网下载:地址:https://dev.mysql.com/downloads/mysql/ [x] 百度云盘 ...

  4. Gin 如何动态生成模型 swagger 文档

    在做 API 接口开发时, 一般会统一 API 返回格式, 例如 { "code": 200, "data": { //xxxxx //xxxxx }, &qu ...

  5. Python 3 快速入门 2 —— 流程控制与函数

    本文假设你已经有一门面向对象编程语言基础,如Java等,且希望快速了解并使用Python语言.本文对重点语法和数据结构以及用法进行详细说明,同时对一些难以理解的点进行了图解,以便大家快速入门.一些较偏 ...

  6. [APIO2020]有趣的旅途

    注意到第一个点是可以钦定的. 那么我们考虑在重心的子树里反复横跳. 每次选择不同子树里的深度最大的点. 在同一颗子树里可能会在lca处出现问题. 那么我们选择重心,要考虑到会不会出现一颗子树不够选的操 ...

  7. #pragma warning(disable:4996)

    VS使用中常常会遇到一些过时或者不安全的函数,编译会报错: 错误 C4996 'sscanf': This function or variable may be unsafe. Consider u ...

  8. MYSQL5.8----M2

    mysql> SHOW DATABASES; +--------------------+ | Database | +--------------------+ | information_s ...

  9. R语言与医学统计图形-【10】ggplot2图形映射

    ggplot2绘图系统--图形映射 颜色的映射. #aes中映射变量 ggplot()+geom_point(aes(x=carat,y=price,color='blue'),#color视为单一变 ...

  10. 毕业设计压力测试——jmeter

    ------------恢复内容开始------------ JMeter是一款纯java编写负载功能测试和性能测试开源工具软件.相比Loadrunner而言,JMeter小巧轻便且免费,逐渐成为了主 ...