Codeforces Gym 101480C - Cow Confinement（扫描线+线段树）

题面传送门

题意：

有一个 \(10^6\times 10^6\) 的地图。其中 \(m\) 个位置上有花，\(f\) 个矩形外围用栅栏围了起来。保证 \(f\) 个矩形两两之间没有公共点。

\(q\) 组询问，每组询问给出两个整数 \(x,y\)，求出：

• 从点 \((x,y)\) 出发，只能向下或向右走，不能越过栅栏，总共可以摘到多少朵花。

\(0\leq m,f,q\leq 2\times 10^5\)

先考虑 \(f=0\) 的情况，那就是一个弱智的扫描线。从低往高扫，如果 \((x_i,y_i)\) 有花，那就在 \(y_i\) 位置 \(+1\)。单点修改，区间查询，线段树可以实现。

再考虑 \(f\neq 0\) 的情况，大体思路还是扫描线，不过实现起来细节多了很多。

当我们扫描到一个矩形 \((x_1,y_1),(x_2,y_2)\) 的下边界的时候，我们只需把线段树上 \([y_1,y_2]\) 全部改为 \(0\)，因为这些位置都没有办法再向下走了。

当我们遇到一个有花的位置的时候，比如下图：

如果橘色位置有花，那么这朵花会对这一行绿色位置产生 \(1\) 的贡献。

故如果一朵花的纵坐标为 \(y\)，那么所有纵坐标在 \([pre_y+1,y]\) 的位置的答案都会加 \(1\)。其中 \(pre_y\) 为 \(y\) 之前的墙的位置。

比较麻烦的是遇到矩形的上边界。

还是拿张图来举个例子：

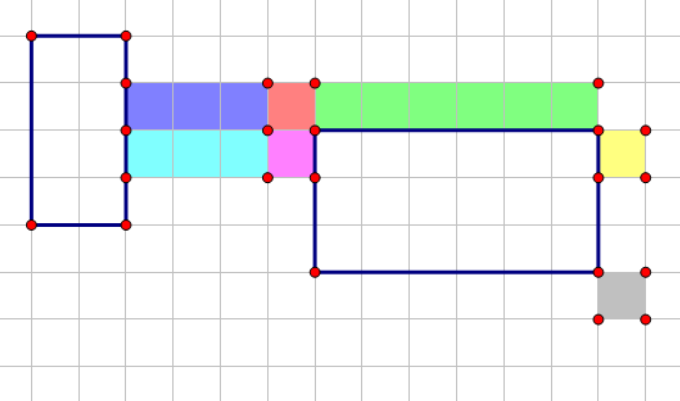
比如说我们现在遇到了右边这个矩形 \((x_1,y_1),(x_2,y_2)\) 的上边界。首先 \([y_1,y_2]\) 内（绿色格子）的位置的答案肯定要发生变化，原先我们计算的是矩形内的答案，现在我们要计算矩形外的答案。稍微观察一下就能发现，这些绿色格子上的答案都等于黄色格子的答案，

除此之外，还有一些格子的值要变化。例如上图中的红色格子，相比于它下方的粉色格子，它既可以向右走，也可以向下走，而从粉色格子只能向下走。多出来的部分就是向右走可以摘到的花朵数。

如果不计当前这一行的贡献的话，那么向右走可以摘到的花朵数就是黄色格子的答案。

但这样算会有重复，有的花既可以通过向下走摘到，也可以通过向右走摘到。这样的花朵的个数其实就是灰色格子的答案。

故红色格子上的答案 \(=\) 粉色格子上的答案 \(+\) 黄色格子上的答案 \(-\) 灰色格子上的答案。

左边三个深蓝色的格子也是如此。

具体来说，假如黄色格子上的答案为 \(x\)，灰色格子上的答案为 \(y\)，那么碰到上边界就需执行以下三个操作：

• \([y_1,y_2]\) 赋上 \(0\)
• \([pre_{y_1-1},y_2]\) 加上 \(x-y\)
• \([y_1,y_2]\) 加上 \(y\)

至于怎样求灰色格子的答案，就直接在扫描到矩阵下边界的时候开个 \(tmp\) 数组记录一下就可以了。

于是这题就分析完了。实现起来还有一个细节要注意：就是你扫描到某一行的时候，执行操作的顺序要注意：一定是先加/删除矩阵，再插入花朵，最后解决询问。加/删除矩阵的顺序就按坐标从小到大排个序。我因此一直 WA 3，花了不少时间调程序。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
	x=0;char c=getchar();T neg=1;
	while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	x*=neg;
}
const int MAXL=1e6;
const int MAXN=2e5;
struct event{
	int opt,x,y,id;
	event(){opt=x=y=id=-1;}
	event(int _opt,int _x,int _y,int _id){
		opt=_opt;x=_x;y=_y;id=_id;
	}
	friend bool operator <(event lhs,event rhs){
		if((lhs.opt>2||rhs.opt>2)&&lhs.opt!=rhs.opt) return lhs.opt<rhs.opt;
		return lhs.x<rhs.x;
	}
};
vector<event> g[MAXL+5];
int F,M,Q;
struct node{
	int l,r,val,lz;
	bool zero;
} s[MAXL*4+5];
void build(int k,int l,int r){
	s[k].l=l;s[k].r=r;if(l==r) return;
	int mid=(l+r)>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
void pushdown(int k){
	if(s[k].zero){
		s[k<<1].zero=s[k<<1|1].zero=1;
		s[k<<1].val=s[k<<1|1].val=s[k].val;
		s[k<<1].lz=s[k<<1|1].lz=s[k].lz;
		s[k].zero=s[k].lz=0;
	}
	if(s[k].lz){
		s[k<<1].val+=s[k].lz;s[k<<1].lz+=s[k].lz;
		s[k<<1|1].val+=s[k].lz;s[k<<1|1].lz+=s[k].lz;
		s[k].lz=0;
	}
}
void modify(int k,int l,int r,int x){
	if(l<=s[k].l&&s[k].r<=r){
		s[k].val+=x;s[k].lz+=x;return;
	} pushdown(k);int mid=(s[k].l+s[k].r)>>1;
	if(r<=mid) modify(k<<1,l,r,x);
	else if(l>mid) modify(k<<1|1,l,r,x);
	else modify(k<<1,l,mid,x),modify(k<<1|1,mid+1,r,x);
	s[k].val=max(s[k<<1].val,s[k<<1|1].val);
}
void assign(int k,int l,int r){
	if(l<=s[k].l&&s[k].r<=r){
		s[k].val=0;s[k].lz=0;s[k].zero=1;return;
	} pushdown(k);int mid=(s[k].l+s[k].r)>>1;
	if(r<=mid) assign(k<<1,l,r);
	else if(l>mid) assign(k<<1|1,l,r);
	else assign(k<<1,l,mid),assign(k<<1|1,mid+1,r);
	s[k].val=max(s[k<<1].val,s[k<<1|1].val);
}
int query(int k,int x){
	if(s[k].l==s[k].r) return s[k].val;
	pushdown(k);int mid=(s[k].l+s[k].r)>>1;
	if(x<=mid) return query(k<<1,x);
	else return query(k<<1|1,x);
}
int ans[MAXN+5],tmp[MAXN+5];
int main(){
	scanf("%d",&F);
	for(int i=1;i<=F;i++){
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		g[x1-1].pb(event(1,y1,y2,i));
		g[x2].pb(event(2,y1,y2,i));
	}
	scanf("%d",&M);
	for(int i=1;i<=M;i++){
		int x,y;scanf("%d%d",&x,&y);
		g[x].pb(event(3,y,-1,-1));
	}
	scanf("%d",&Q);
	for(int i=1;i<=Q;i++){
		int x,y;scanf("%d%d",&x,&y);
		g[x].pb(event(4,y,-1,i));
	}
	multiset<int> wall;wall.insert(-1);
	build(1,0,MAXL+1);
	for(int i=1;i<=MAXL;i++) sort(g[i].begin(),g[i].end());
//	modify(1,1,3,1);modify(1,2,4,1);assign(1,3,3);modify(1,1,5,1);
//	modify(1,2,6,1);assign(1,2,4);modify(1,4,5,1);
//	for(int i=1;i<=6;i++) printf("%d\n",query(1,i));
	for(int i=MAXL;i;i--){
		for(int j=0;j<g[i].size();j++){
			if(g[i][j].opt==1){
				assign(1,g[i][j].x,g[i][j].y);
				wall.erase(wall.find(g[i][j].x-1));
				wall.erase(wall.find(g[i][j].y));
				int x=query(1,g[i][j].y+1);
				modify(1,(*--wall.lower_bound(g[i][j].x))+1,g[i][j].y,x-tmp[g[i][j].id]);
				modify(1,g[i][j].x,g[i][j].y,tmp[g[i][j].id]);
			} else if(g[i][j].opt==2){
				assign(1,g[i][j].x,g[i][j].y);
				wall.insert(g[i][j].x-1);
				wall.insert(g[i][j].y);
				tmp[g[i][j].id]=query(1,g[i][j].y+1);
			} else if(g[i][j].opt==3){
//				printf("%d %d %d\n",(*--wall.lower_bound(g[i][j].x))+1,g[i][j].x,1);
				modify(1,(*--wall.lower_bound(g[i][j].x))+1,g[i][j].x,1);
			} else {
				ans[g[i][j].id]=query(1,g[i][j].x);
//				printf("%d\n",g[i][j].x);
			}
		}
	}
//	for(int i=1;i<=F;i++) printf("%d\n",tmp[i]);
	for(int i=1;i<=Q;i++) printf("%d\n",ans[i]);
	return 0;
}
/*
4
2 2 8 4
1 9 4 10
6 7 9 9
3 3 7 3
9
3 4
8 4
11 5
10 7
10 8
9 8
2 8
4 11
9 11
8
1 1
5 10
6 9
3 7
7 1
4 2
7 5
3 3
*/