JAVA实现表达式求导运算的分析总结

1第一次作业

1.1题目描述

　　对形如4*x+x^2+x的多项式求导。

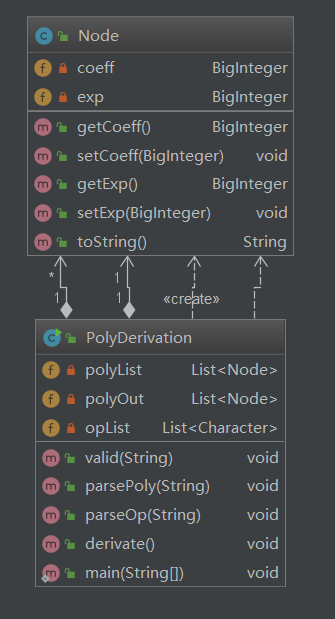
1.2类图

1.3度量分析

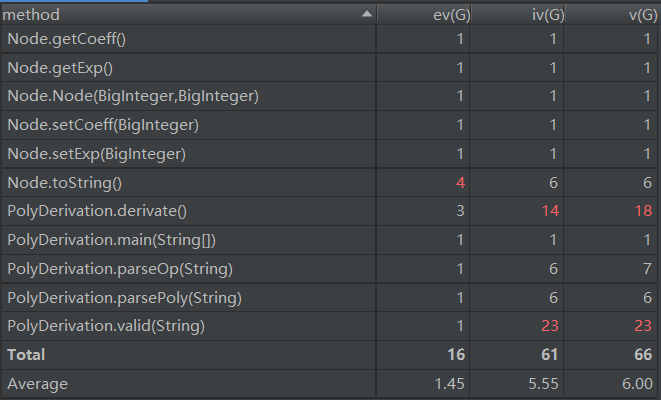
　　在完成第一次作业时，我的写法没有特别的“面向对象”。唯一封装起来的是Node，代表多项式的一个项。PolyDerivation是一个方法庞杂的类，先判断输入是否合法，再将多项式拆分成独立的项，接着求导，同时也包含了程序的入口main。这无疑是一个面向方法的写法。

　　写valid方法判断合法性的时候，经历过一次波折。一开始的思路是用一个很长的大正则表示出整个多项式，写完发现超过了100个字符，很不美观。而且如果表达式的项数过多，递归层数太深会爆栈。然后我换了一种思路，正则每次只匹配一个项，而项又可以根据x有没有系数和指数分为5类，所以我一共写了5种很短的正则分别匹配5种项。

　　但是我有一个地方多此一举了。就是用parsePoly和parseOp两个方法分别取得独立的项和他们之前的符号。其实连接各个项的符号可以归并到每个项里。

1.4BUG分析

　　我公测和互测阶段都没有bug。其实提交之前，我改了很多自己的bug。比如优化之后，出现了求导之后如果约掉了所有项就没有输出的情况。

　　互测阶段，我hack到别人的bug有爆栈，特殊空白字符，化简之后格式错误这三类问题。

2第二次作业

2.1题目描述

　　增加sin(x)和cos(x)，每个乘积项可以有多个因子。

　　样例：cos(x)*sin(x)*5+x^233+sin(x)^+2

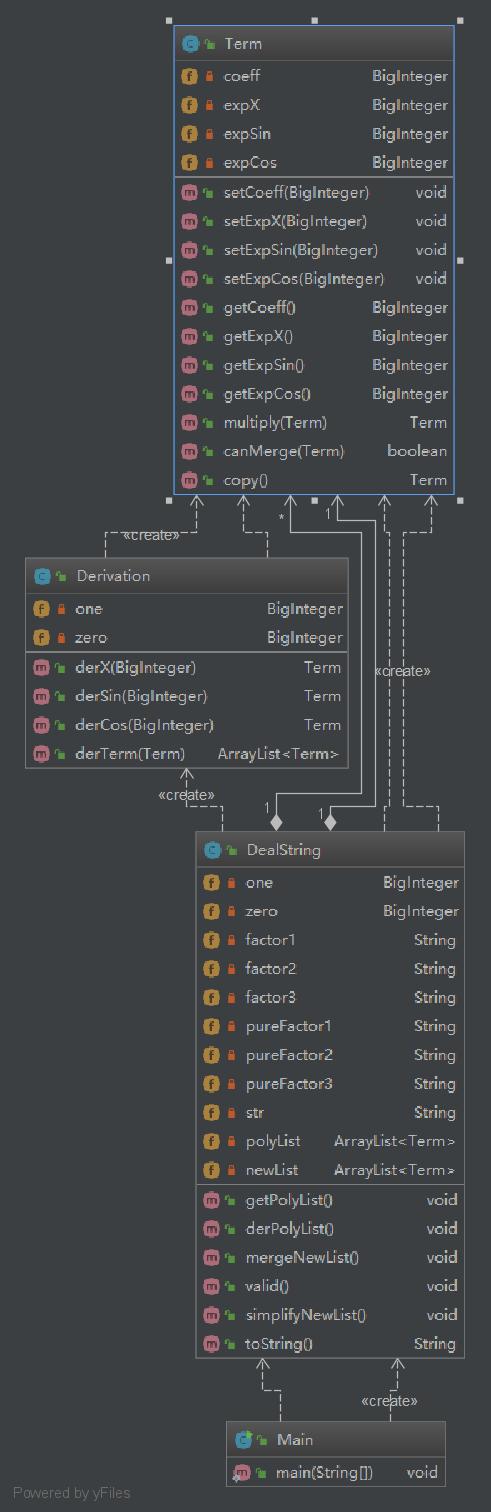
2.2类图

2.3度量分析

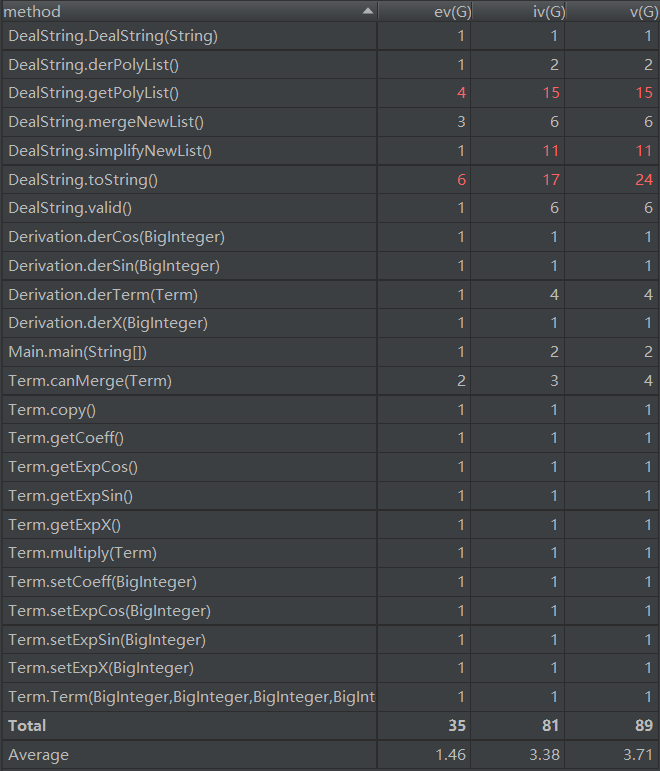
　　多项式的每一个乘积项其实只有四种因子：常数，x，sin(x)，cos(x)。延续作业一的思想，我把乘积项封装在Term类里面，有四个重要属性，分别为常数项和后三种因子的指数。为了保留一个简洁的main入口，我设置了一个只包含main方法的Main类。需要对字符串进行三步处理，即合法判断，拆分乘积项，和求导，这些方法都放在了另一个类DealString里面。Derivation类实现了对x和三角函数的幂求导，他没有属性，只有方法，在需要使用他的功能时创建一个引用，然后直接调用他的方法即可。

　　第二次作业我把精力放在了结果化简上面。除了合并同类项，sin(x)^2+cos(x)^2也可以化简。每一次对三角函数化简之后得到的新项，可能会继续满足化简条件。所以我使用for循环，并设置flag记录某次遍历有没有化简出新的项，直到不能再化简为止就停止遍历。

2.4BUG分析

　　我通过了所有公测，但是互测被hack了合法性判断问题，我有一处正则表达式漏掉了一个空白字符。

　　互测时使用了shell脚本，可以同时输出小组内所有人的求导结果。结合matlab，可以很快判断他们的运算结果是否正确。我是这样使用matlab的：

>>x=2
sin(x)+3*x^2

1*sin(x)^1+3*x^2

......

3*x^2+sin(x)

　　先设置x的值，后面粘贴同组人输出结果，敲击回车，比较数值是否一致。

3第三次作业

3.1题目描述

　　增加多项式因子，sin(...)和cos(...)内部可以嵌套因子。

　　样例：sin((2*x))^2*(cos(x)+1)

3.2类图

3.3度量分析

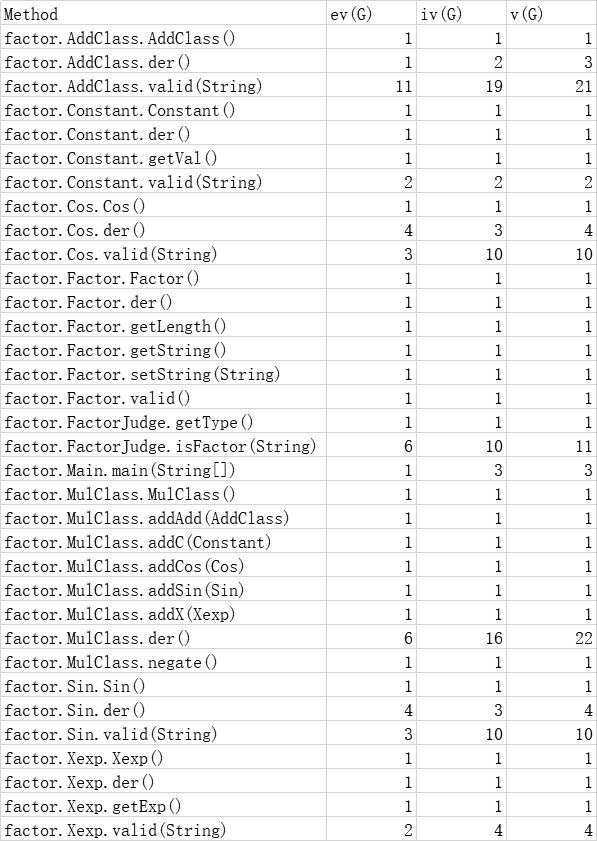
　　Factor类代表了因子，它有常数，x的幂，sin的幂，cos的幂，乘类，加类，这6个子类。他们都重写了合法性判断和求导的方法。

　　第三次作业与前两次最大的不同是，采用了继承的结构，将合法性判断和求导交给不同的因子类自行解决。

　　合法性判断思路：对于常数，x的幂，sin，cos因子，valid方法的传入参数是一个长字符串，应该判断字符串的前缀是否为合法因子。如果包含则返回true，并且捕获前缀中的相关信息，初始化这个因子类的属性（指数等）。对于加类，需要从头至尾地判断传入字符串是否为合法的AddClass类，而不仅仅是前缀。具体方法是判断前缀是否为一个合法的因子，其后如果是*（乘号），把该因子加入到动态创建的MulClass实例的属性里，如果是+-号，把这个mulClass加入到这个加类的ArrayList<MulClass>里。一边判断合法性，一边存储合法因子。

　　求导思路：根据乘积和嵌套的求导法则，分别调用所包含的因子实例的求导参数。结果返回一个字符串。

　　下表为不同因子之间的包含关系：

类名	属性
AddClass	ArrayList<MulClass>
MulClass	BigInteger coeff BigInteger xexp ArrayList<Sin> ArrayList<Cos> ArrayList<AddClass>
Sin	BigInteger exp AddClass inside
Cos	BigInteger exp AddClass inside
Xexp	BigInteger exp
Constant	BigInteger val

　　其中加类AddClass比较特殊，输入的多项式就是一个加类，带括号的多项式因子也是一个加类。

3.4BUG分析

　　强测多个点超时，受到了毁灭性打击。以上的类图是在bug修复环节我重构一遍的架构，不会超时。重构之前的加类里面，我用for循环扫描字符串从start到end的子串是不是合法因子，如果不是就end++，再判断一次；如果是就start=end+1，判断后续因子。这个办法for循环层数很深，处理((((((((x))))))))这种多层括号的数据点时很容易超时。

　　互测hack别人的数据点大多数是导数计算错误，少数优化的很好的同学存在过度化简问题（比如输出sin(2*x)）。

4问题反思

4.1方法过长

　　checkstyle要求方法长度不超过60行，我超长的方法内基本都有一个很长的while循环。我的解决方式是将while内部，功能相对独立的语句合并成一个新的方法。即将大方法的步骤分化成小方法，并在大方法里调用小方法。

4.2大段重复代码

　　sin和cos这两个类极为相像，因此有很多重复的代码。我目前的思路是给他们一个共同的Tri父类，将原来重复的代码放在父类里面实现，子类只体现区别。