第五课第四周笔记2：Self-Attention 自注意力

Self-Attention 自注意力

让我们跳进去谈谈transformer的self-attention机制。如果您能了解本视频背后的主要思想，您就会了解变压器网络工作背后最重要的核心思想。

让我们开始吧。您已经看到了注意力如何与诸如 RNN 之类的顺序神经网络一起使用。要使用更晚的 CNN 风格的注意力，您需要计算自注意力，在其中为输入句子中的每个单词创建基于注意力的表示。让我们使用我们的运行示例，Jane、visite、l'Afrique、en、septembre，我们的目标是为每个单词计算这样的基于注意力的表示。所以我们最终会得到其中的五个，因为我们的句子有五个单词。当我们计算它们时，我们将这五个词用 A1 到 A5 表示。我知道您开始看到一堆符号 Q、K 和 V，我们将在稍后的幻灯片中解释这些符号的含义，所以现在不要担心它们。

我将要使用的运行示例是在这句话中使用 l'Afrique 一词。我们将在下一张幻灯片中逐步介绍 Transformer 网络的自注意力机制如何允许您为这个单词计算 A3，然后您也对句子中的其他单词执行相同的操作。

现在您之前学习了词嵌入。表示 l'Afrique 的一种方法是查找 l'Afrique 的词嵌入。但是，根据上下文，我们是否将 l'Afrique 或Africa视为具有历史意义的地点或度假胜地，或者是世界第二大洲。根据您对 l'Afrique 的看法，您可以选择以不同的方式表示它，这就是表示 A(3) 的作用。它将查看周围的词，试图找出我们在这句话中谈论Africa的实际情况，并为此找到最合适的表示。就实际计算而言，它与您之前看到的在 RNN 上下文中应用的注意力机制不会有太大区别，除了我们将对句子中的所有五个单词并行计算这些表示。当我们在 RNN 之上建立注意力时，这就是我们使用的等式。

使用自注意力机制，注意力方程看起来像这样。你可以看到方程有一些相似之处。这里的内部项也涉及一个 softmax，就像左边的这个项一样，你可以将指数项视为类似于注意力值。您将在下一张幻灯片中看到这些术语的确切计算方式。所以，再一次，不要担心细节。

但主要区别在于，对于每个单词，比如 l'Afrique，您都有三个值，称为查询(q)、键(k)和值(v)( query, key, and value)。这些向量是计算每个词的注意力值的关键输入。

现在，让我们逐步完成实际计算 A3 所需的步骤。在这张幻灯片上，让我们逐步完成从单词 l'Afrique 到自注意力表示 A3 所需的计算。作为参考，我还在右上方打印了上一张幻灯片中类似 softmax 的方程。首先，我们要将每个单词与称为query(q), key(k), value(v)对的三个值相关联。如果 X3 是 l'Afrique 的词嵌入，则 q3 的计算方式是作为学习矩阵，我将写成 WQ 乘以 X3，对于键值对也类似，所以 k3 是 WK 乘以 x3，v3 是 WV 乘以 x3。这些矩阵 WQ、WK 和 WV 是此学习算法的参数，它们允许您为每个单词提取这些查询、键和值向量。

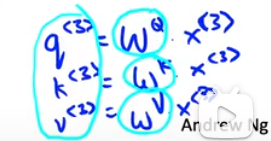
那么这些查询键和值向量应该做什么呢？他们确实使用了一个类似于音乐会和数据库的松散类比，您可以在其中进行query, key, value对。如果您熟悉这些类型的数据库，这个类比可能对您有意义，但如果您不熟悉该数据库概念，请不要担心。让我给出这些查询、键和向量值的意图背后的一种直觉（请结合下图）。

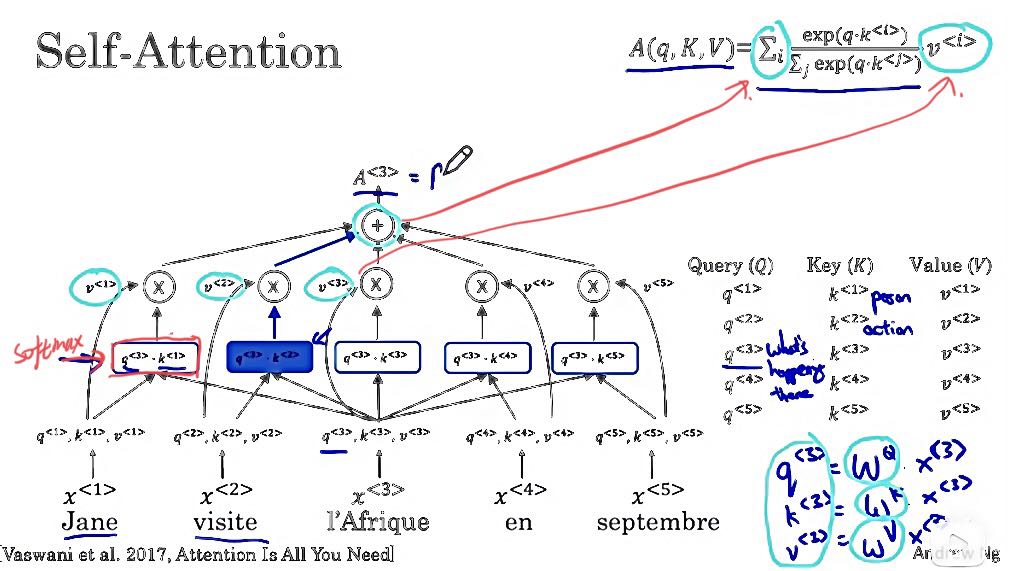
1. Q3 是一个关于 l'Afrique 的问题。 Q3 可能代表一个问题，比如那里发生了什么？Africa，l'Afrique 是一个目的地。您可能想知道在计算 A^3 时，那里发生了什么。我们要做的是计算 q^3 和 k^1 之间的内积。

2. 然后我们计算 q^3 和 k^2 之间的内积，此操作的目标是提取所需的最多信息，以帮助我们在这里计算最有用的表示 A^3。

3. 再次，只是为了建立直觉，如果 k^1 代表这个词是一个人，因为 Jane 是一个人，而 k^2 代表第二个词，visite，是一个动作，那么你可能会发现 q^3 与k^2 的内积值最大，这可能是直观的例子，可能表明visite 为您提供与Africa正在发生的事情最相关的上下文。也就是说，它被视为访问的目的地。

4. 我们要做的是在这一行中取这五个值并计算它们的 Softmax。这里其实有这个Softmax，在我们刚才讲的例子中，q^3 乘以k^2 对应wordvisite 可能是最大的值。用蓝色表示。最后，我们将取这些 Softmax 值并将它们与 v^1 相乘，v^1 是单词 1 的值，单词 2 的值，依此类推，因此这些值对应于那里的值。

5. 最后，我们总结一下。这个求和对应于这个求和运算符，因此将所有这些值相加得到 A^{3，它正好等于这里的这个值。另一种写A}3的方式实际上是A(q^3，k，v) 。但有时这样写A^3会更方便。这种表示的主要优点是 l'Afrique 的词不是一些固定的词嵌入。相反，它让自注意力机制意识到 l'Afrique 是访问者、访问的目的地，从而为这个词计算更丰富、更有用的表示。
   
   

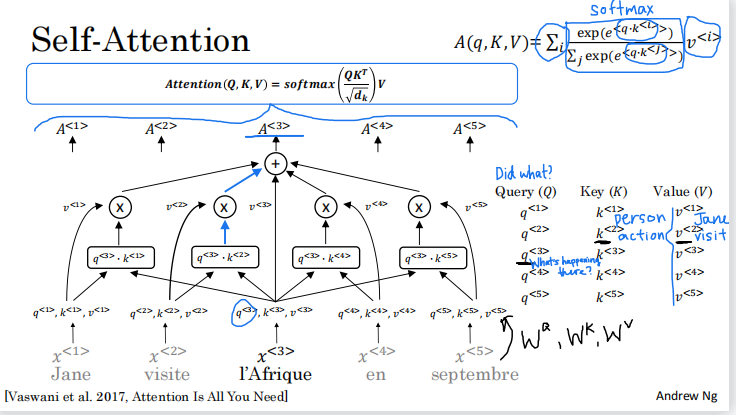
现在，我一直在使用第三个单词 l'Afrique 作为运行示例，但您可以对序列中的所有五个单词使用此过程，以获得类似 Jane、visite、l'Afrique、en、septembre 的丰富表示。如果把这五个计算放在一起，文献中使用的外延是这样的，你可以把我们刚刚谈到的所有这些计算对序列中的所有单词进行总结，写成Attention(Q, K, V) where Q , K, V 矩阵具有所有这些值，这只是这里方程的压缩或矢量化表示。分母的式子只是为了缩放点积，因此它不会爆炸。你真的不需要担心它。但这种注意力的另一个名称是缩放点积注意力。这就是最初的 Transformer 架构论文《Attention Is All You Need》中所代表的内容。这就是transformer网络的self-attention机制。

概括地说，与五个词中的每一个相关联，您最终会得到一个查询q、一个键k和一个值v。该查询让您可以提出有关该词的问题，例如Africa正在发生的事情。关键字查看所有其他单词，并根据与查询的相似性，帮助您找出哪些单词给出了与该问题最相关的答案。在这种情况下，visite 是在Africa发生的事情，某人正在访问Africa。

最后，该值允许表示插入访问者应如何在 A^3 内表示，在Africa的表示内。这使您可以为Africa这个词提出一个表示，表示这是Africa并且有人正在访问Africa。您只需要为每个单词提取相同的固定词嵌入而不能够根据其左侧和右侧的词进行调整相比，这是对世界的一种更细致、更丰富的表示单词。我们都必须考虑到上下文。