Coursera Deep Learning笔记 改善深层神经网络：超参数调试 Batch归一化 Softmax

摘抄：https://xienaoban.github.io/posts/2106.html

1. 调试(Tuning)

超参数	取值
#学习速率：\(\alpha\)
Momentum：\(\beta\)	0.9:相当于10个值中计算平均值；0.999相当于1000个值中计算平均值
Adam：\(\beta_1\)	0.9
Adam：\(\beta_2\)	0.999
Adam：\(\varepsilon\)	\(10^{-8}\)
#layers
#hidden unit
#mini-batch size

参数选择有以下一些方法:

1. 随机选择点。例如现在有 \(α\) 与 Adam 的 \(ε\) 两个超参数要调试。在参数取值范围内随机选择若干点， 可以发现哪个超参数更重要，影响更大.

2. 由粗糙到精细的策略。由1， 发现在某个点效果最好，可以预测在该点附近效果也很好，于是放大这块区域, 更密集地取值.
   
   

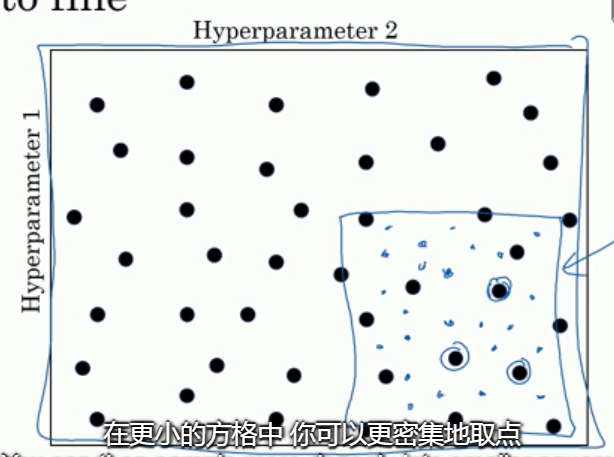
3. 随机选择点时，有些参数不适合均匀(在线性轴上)的随机选择. 例如 \(\alpha\)，我们希望其在对数轴上随机取点(0.0001, 0.001, 0.01, 0.1, 1)，我们可以 a = 10**(-4*np.random.rand())，即可得到 \(a\in[10^{−4},10^0]\)

4. 对 \(\beta\) 取点，比如 \(\beta\)=0.9...0.999，\(1-\beta\) = 0.1...0.001， \(1-\beta\in[10^{−3},10^{-1}]\)

2. Batch 归一化(Batch Norm)

会使你的参数搜索问题变的容易，使神经网络对超参数的选择更加稳定，超参数的范围会更庞大，学习算法运行速度更快

2.1 实现

训练 Logistic 回归时, 归一化 \(X\) 可以加快学习过程. 现在我们希望对隐藏层的 \(Z\) 归一化. (或者 \(A\))

对每一层的\(z\), \(a\) 做如下操作:

\[平均值:\mu = \frac{1}{m} \sum_i z^{(i)} \\
方差:\sigma^2 = \frac{1}{m} \sum_i (z^{(i)} - \mu)^2 \\
z_{\text{norm}}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}} \\
\widetilde{z}^{(i)} = \gamma z_{\text{norm}}^{(i)} + \beta
\]

(ε是为了防止分母为0.)

• \(z_{norm}\) 就是标准化的 \(z\), \(z\)的每一个分量都含有 平均值为0, 方差为1。

• 不想让隐藏单元总是含有平均值0和方差1（也许隐藏单元有了不同的分布会有意义）, 计算 \(\widetilde{z}\).

• \(\gamma\) 与 \(\beta\) 是模型的学习参数, 梯度下降时会像更新神经网络的权重一样更新 \(\gamma\) 和 \(\beta\)。\(\gamma\) 与 \(\beta\) 的作用是：可以随意设置 \(\widetilde{z}^{(i)}\) 的平均值。当 \(\gamma = \sqrt{\sigma^2+\varepsilon}\) 且 \(\beta = \mu\) 时，\(\widetilde{z}^{(i)} = z^{(i)}\)， 通过赋予 \(\gamma\) 和 \(\beta\) 其他值，可以使你构造含其他 平均值 和 方差 的隐藏单元值。

• Batch归一化的作用：是它适合的归一化过程不只是输入层， 同样适用于神经网络中的深度隐藏层。Batch归一化了一些隐藏单元值中的平均值和方差。

2.2 将Batch Norm拟合进神经网络

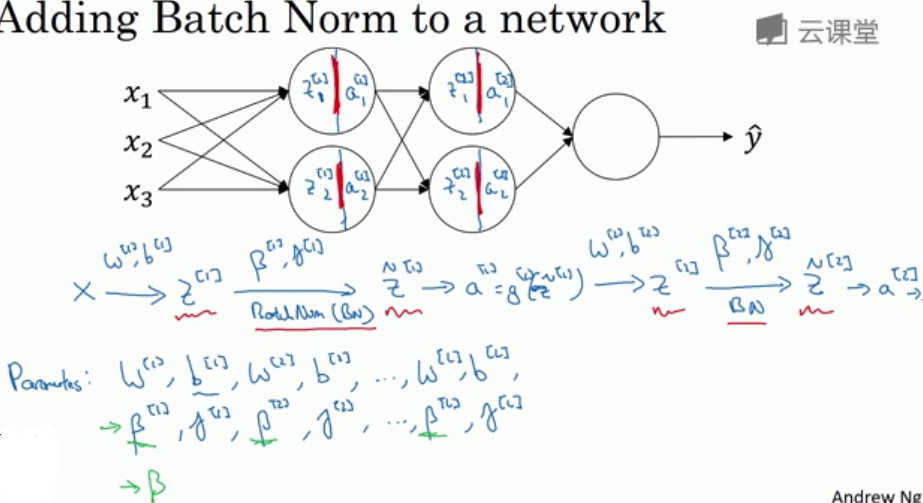
• 使用该方法时, 参数 w 和 b 中的 b 可以不设立, 毕竟 b 总是会被归一化减去. 于是参数只剩下了 \(w\), \(\beta\), \(\gamma\).

2.3 Batch Norm为什么奏效？

• Batch 归一化减少了输入值改变的问题, 它使这些值变得更稳定,（例如：无论\(z^{[1]}\),\(z^{[2]}\)如何变化，他们的均值和方差保持不变），它减弱了 前层参数的作用 与 后层参数的作用 之间的联系, 它使得网络每层都可以自己学习, 稍稍独立于其它层, 有助于加速整个网络的学习.

• 另外, 每个 mini-batch 子数据集的均值和方差均有一些噪音, 而 Batch 归一化将 \(z\) 缩放到 \(\widetilde{z}\) 的过程也有噪音, 因此有轻微的正则化效果.

• 训练时，\(\mu\) 和 \(\sigma^2\) 是在整个 mini-batch 上计算出来的（包含了像是64或28或其他一定数量的样本）；测试时，你可能需要逐一处理样本，方法是根据你的训练集估算 \(\mu\) 和 \(\sigma^2\)，通常运用 指数加权平均 来追踪在训练过程中的 \(\mu\) 和 \(\sigma^2\)。

  • 在测试时, 我们很可能只想测一个样本, 此时 均值 \(\mu\) 和 方差 \(\sigma\) 没有意义. 因此我们要使用估算的 \(\mu\) 和 \(\sigma\) 进行测试.

3. Softmax 回归

类似 Logistic 回归, 但 Softmax 回归能识别多个分类. 因此 \(\hat{y}\) 是 C×1 维的向量, 给出 C 个分类的概率,所有概率加起来应该为1.

在神经网络的最后一层, 我们像往常一样计算各层的线性部分, 当计算了 \(z^{[L]} = W^{[L]}a^{[L-1]}+b^{[L]}\) 之后, 使用 Softmax 激活函数.

\[a^{[L]}_i = \frac{e^{z^{[L]}_i}}{\sum_{j=1}^{4} e^{z^{[L]}_i}}
\]

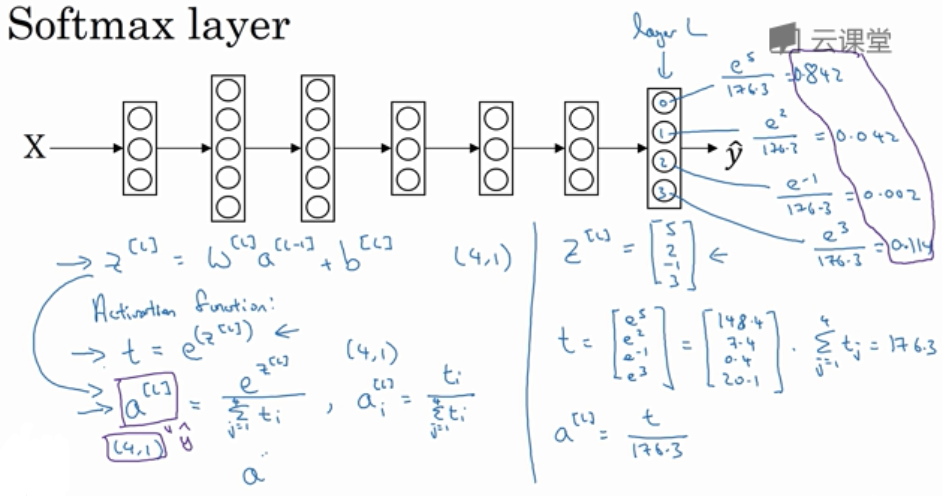
Softmax 分类中, 一般使用的损失函数及反向传播的导数是

\[L(\hat{y}, y) = -\sum_{j=1}^{n}y_j \text{log } \hat{y}_j \\
J(w^{[1]}, b^{[1]}, ...) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) \\
\frac{\partial J}{\partial z^{[L]}} = \hat{y} - y
\]

Softmax 给出的是每个分类的概率. 而对应的 Hardmax 则是将最大的元素输出为 1, 其余元素置 0.