LTI系统对WSS Processes的作用

本文主要专注讨论LTI系统对WSS Process的影响。WSS Process的主要特性有mean以及correlation，其中correlation特性在滤波器设计，信号检测，信号预测以及系统识别中扮演者非常重要的作用。

LTI系统的数学式由卷积定义，假设LTI系统的脉冲响应为$h(t)$，输入的WSS Process为$x(t)$，输出的Process为$y(t)$，那么有如下公式：

$\displaystyle{y(t) = \int_{-\infty}^{+\infty}h(v)x(t-v)dv=\int_{-\infty}^{+\infty}x(v)h(t-v)dv}$

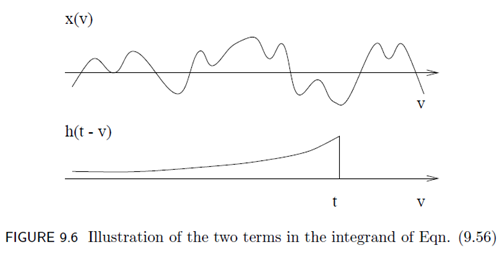
对于一个稳定的LTI系统来说，只要输入是有界的，那么输出也是有界的（BIBO）。不过我们这里的输入的是WSS Process，不同于固定的输入信号，比起要求每一个采样点上的输入都有界，要求$E[x^2(t)]=R_{xx}(0)$是有界的就足够了。（白噪声是特殊情况）

Mean/Expectation

WSS Processes在通过LTI系统之后，该process的mean为

$\begin{align*}
\mu_y = E[y(t)] &= E\left\{ \int_{-\infty}^{+\infty}h(v)x(t-v)dv \right\}\\
&=\int_{-\infty}^{+\infty}h(v)E[x(t-v)]dv\\
&=\int_{-\infty}^{+\infty}h(v)\mu_x dv\\
&=\mu_x \int_{-\infty}^{+\infty}h(v)dv\\
&=H(j0)\mu_x
\end{align*}$

这意味着输出的mean也是一个常数$\mu_y$，输入输出的mean相差的倍数为$\frac{\mu_y}{\mu_x} = H(j0)$，这个数值是该连续时间LTI系统的频率响应$H(j\Omega)$在零点处的取值，我们也可以把它称为该LTI系统的DC增益（DC gain）。

Cross-correlation

WSS Process在LTI系统的输入输出有cross-correlation如下

$\begin{align*}
E\{y(t+\tau)x(t)\} &= E\left\{ \left[\int_{-\infty}^{+\infty}h(v)x(t+\tau-v)dv \right ]x(t)\right \}\\
&=\int_{-\infty}^{+\infty}h(v)E\Big\{x(t+\tau-v)x(t)\Big\}dv\\
&=\int_{-\infty}^{+\infty}h(v)R_{xx}(\tau-v)dv \qquad x(t)\ is\ WSS\ Process\\
&=h(\tau)*R_{xx}(\tau) \qquad this\ crosscorrelation\ is\ only\ relevant\ to\ \tau\\
&=R_{yx}(\tau)
\end{align*}$

从上面的式子也能得到如下关系：

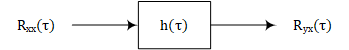
输入输出的process之间的cross-correlation只与两者的时间延迟$\tau$有关。

另外，根据WSS的相关性质，还可以得到

$R_{xy}(\tau)=R_{yx}(-\tau)=R_{xx}(-\tau)*h(-\tau)=R_{xx}(\tau)*h(-\tau)$

Auto-correlation

WSS Process在LTI系统的输出有auto-correlation如下

$\begin{align*}
E\{y(t+\tau)y(t)\} &= E\left\{ \left[\int_{-\infty}^{+\infty}h(v)x(t+\tau-v)dv \right ]y(t)\right \}\\
&=\int_{-\infty}^{+\infty}h(v)E\Big\{x(t+\tau-v)y(t)\Big\}dv\\
&=\int_{-\infty}^{+\infty}h(v)R_{xy}(\tau-v)dv \\
&=h(\tau)*R_{xy}(\tau) \qquad this\ autocorrelation\ is\ only\ relevant\ to\ \tau\\
&=R_{yy}(\tau)
\end{align*}$

从上面的式子也能得到如下关系：

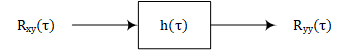
WSS Process在经过LTI系统后所得到的输出的auto-correlation仅与时间差$\tau$有关，并且前面也提到该输出process的mean是固定常数，因此输出仍然是WSS Process。

Jointly WSS

由于LTI系统的输入$x(t)$与输出$y(t)$都是WSS·Process，并且这两者的cross-correlation只与时间差$\tau$有关，因此$x(t)$与$y(t)$是Jointly WSS的。

Summary

Continuous-Time

前面我们已经得出WSS process在经过LTI系统时的mean特性:

$\mu_y=H(j0)\mu_x$

correlation特性：

$\begin{align*}
R_{yx}(\tau)&=h(\tau)\ * \ R_{xx}(\tau)\\
R_{xy}(\tau)&=h(-\tau) * \ R_{xx}(\tau)\\
R_{yy}(\tau)&=h(\tau)\ * \ R_{xy}(\tau)
\end{align*}$

另外，covariance与correlation之间有关系$C_{x,y}(t+\tau,t) = R_{x,y}(t+\tau,t) + \mu_x(t+\tau)\mu_y(t)$，并且此处$x(t),y(t)$均为WSS Process，因此有如下covariance特性：

$\begin{align*}
C_{yx}(\tau)&=h(\tau)\ * \ C_{xx}(\tau)\\
C_{xy}(\tau)&=h(-\tau) * \ C_{xx}(\tau)\\
C_{yy}(\tau)&=h(\tau)\ * \ C_{xy}(\tau)
\end{align*}$

通过上面的特性也能得到：

$\begin{align*}
R_{yy}(\tau)&=R_{xx}(\tau)*\underbrace{h(\tau) * h(-\tau)}_{h(\tau) * h(-\tau)\triangleq\overline{R}_{hh}(\tau)}&=R_{xx}(\tau)*\overline{R}_{hh}(\tau) \\
C_{yy}(\tau)&=C_{xx}(\tau)*\underbrace{h(\tau) * h(-\tau)}_{h(\tau) * h(-\tau)\triangleq\overline{R}_{hh}(\tau)}&=C_{xx}(\tau)*\overline{R}_{hh}(\tau)
\end{align*}$

在式子当中，我们定义了$\overline{R}_{hh}(\tau)$表示为LTI系统脉冲响应$h(\tau)$与其对称函数进行卷积，有

$\displaystyle{\overline{R}_{hh}(\tau)=h(\tau)*h(-\tau) = \int_{-\infty}^{+\infty}h(t+\tau)h(t)dt}$

我们把$\overline{R}_{hh}(\tau)$称为deterministic autocorrelation function of $h(t)$。

而在频域，令$S_{xx}(j\Omega) = \mathcal{F}\Big(R_{xx}(\tau)\Big)$，有

$\begin{align*}
S_{yx}(j\Omega)&=H(j\Omega) \ S_{xx}(j\Omega)\\
S_{xy}(j\Omega)&=H^*(j\Omega)  S_{xx}(j\Omega)\\
S_{yy}(j\Omega)&=H(j\Omega) \ S_{xy}(j\Omega)
\end{align*}$

※$h(t)$是实函数，那么$h(-t)$的傅里叶变换就是$H(j\Omega)$的复共轭，即$H^*(j\Omega)$，并且有$H(j\Omega)H^*(j\Omega) = |H(j\Omega)|^2$。

同时也能推导出

$S_{yy}(j\Omega) = S_{xx}(j\Omega) H(j\Omega) H^*(j\Omega) = S_{xx}(j\Omega)|H(j\Omega)|^2$

Discrete-Time

同理，我们在离散时间的信号与系统中，可以得到

Mean：

$\displaystyle{\mu_y = \mu_x\sum_{-\infty}^{\infty}h[n]}$

Correlation:

$\begin{align*}R_{yx}[m] &= h[m]*R_{xx}[m]\\
R_{xy}[m] &= h[-m]*R_{xx}[m]\\
R_{yy}[m] &= h[m]*R_{xy}[m]\\
R_{yy}[m] &= h[m]*h[-m]*R_{xx}[m] = \overline{R}_{hh}[m]*R_{xx}[m]
\end{align*}$

其中$\overline{R}_{hh}[m]$为$h[m]$的deterministic autocorrelation function，定义如下

$\displaystyle{ \overline{R}_{hh}[m] = h[m]*h[-m]=\sum_{-\infty}^{\infty}h[n+m]h[n] }$

上述关系式的傅里叶变换以及z变换有如下关系

$\begin{align*}
\mu_y &= H(e^{j0})\mu_x ,& S_{yx}(e^{j\Omega})&=S_{xx}(e^{j\Omega})H(e^{j\Omega}), &S_{yy}(e^{j\Omega})&=S_{xx}(e^{j\Omega})|H(e^{j\Omega})|^2\\
\mu_y &= H(1)\mu_x ,& S_{yx}(z)&=S_{xx}(z)H(z) ,& S_{yy}(z)&=S_{xx}(z)H(z)H(1/z)
\end{align*}$

※$h[m]$是实数序列，因此才可以得到$H(e^{j\Omega})H(e^{-j\Omega}) = |H(e^{j\Omega})|^2$。

以上correlation式子也能写成covariance式子（略）。

Reference：

Alan V. Oppenheim: Signals, Systems and Inference, Chapter 9:Random Process