[C++]动态规划系列之Warshall算法

/**
 *
 * @author Zen Johnny
 * @date 2018年3月31日 下午8:13:09
 *
 */
package freeTest;
/*
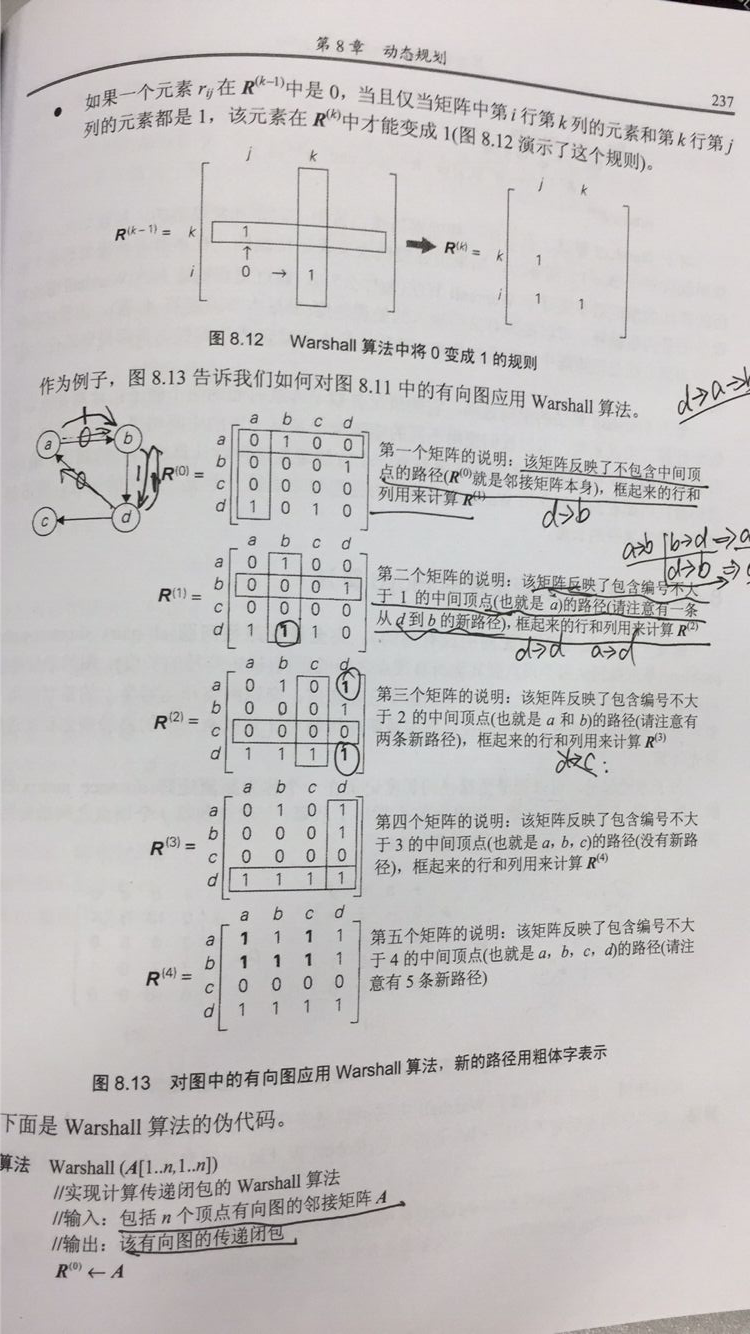
     【动态规划系列:Warshall算法】
 
    问题定义：
    一个顶点有向图的传递闭包可以定义为一个n阶布尔矩阵T={t(i,j)}；
    如果从第i个顶点之间存在一条有效的有向路径（即 长度大于0的有向路径），
    矩阵第i行（1<=i<=n）第j列（1<=j<=n）的元素为1，否则为，t(i,j)为0
 
    问题：计算有向图内各点传递闭包(可达矩阵).
 
    思路：利用中间顶点，遍历以中间顶点为点的所有可达的路径；共计n趟。
*/
 
public class Warshall {
 
    public static void print(int graph[][]) {
        for(int i=0,len_side = graph.length;i<len_side;i++) {
            for(int j=0;j<len_side;j++) {
                System.out.printf("%d ", graph[i][j]);
            }
            System.out.println();
        }
    }
 
    public static int[][] warshall (int graph[][]) {
        for(int i=0,len_side = graph.length;i<len_side;i++) {
            for(int j=0;j<len_side;j++) {
                if(graph[i][j]!=0) {
                    for(int k=0;k<len_side;k++) {
                        if(graph[k][i]!=0)
                            graph[k][j] = 1;
                    }
                }
            }
        }
        return graph;
    }
 
    public static void main(String args[]) {
        int [][] graph = new int[][] {
            {0,1,1,0},
            {0,0,0,1},
            {0,0,0,0},
            {1,0,1,0}
        };
        print(warshall(graph));
    }
 
}

Output:

1 1 1 1
1 1 1 1
0 0 0 0
1 1 1 1