RMQ问题--范围最小值问题

范围最小值问题（Range Minium Query,RMQ）---RMQ问题

一、一维问题

给出一个n个元素的数组A₁,A₂,...,An,

设计一个数据结构，

支持查询操作Query（L,R）：计算min（A_L,A_L+1,...A_R）

显然，

用一个循环来计算最小值

显然不够快，

即使是前缀和的思想也不能提高效率！

那么，

实践中最常用的是Tarjan的Sparse-Table算法（就是ST表）

预处理时间：O（nlogn）

查询时间：O（1）

（这个算法非常好写，而且还不容易出错）

（其实：RMQ问题可以做到O（n）预处理，O（1）查询，但，我不会，嘻嘻，蒟蒻本质）

--------------------------------------------------------

ST表：

用的是倍增的思想

用来求区间最值问题

（ST表即可以求最大值，又可以求最小值；但RMQ问题只需要求区间最小值，所以，可以说是，用ST这种算法来解决RMQ问题）

令d（i，j）表示从i开始的，长度为2^j的一段元素中的最小值；

那么，就可以用递推的方法计算

　　d（i，j）=min{d（i，j-1），d（i+2^j-1，j-1）}

原理如下

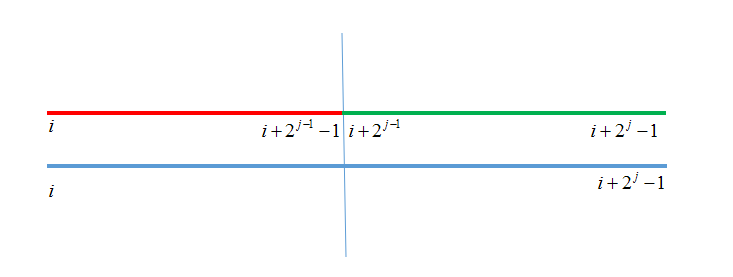
时间复杂度分析：

　　2^j<=n;因此d数组的元素个数不超过nlogn，而每一项都可以在常数时间计算完毕，故总时间为O（nlogn）

代码：

void RMQ_init(const vector<int>& A)
{
    int n = A.size();
    for(int i = ;i < n;i++)
        d[i][] = A[i];
    for(int j = ;( << j) <= n;j++)
        for(int i = ;i + (<<j) -  < n;i++)
            d[i][j] = min(d[i][j-],d[i + (<<(j-))][j-]);
}

上面这是预处理的操作

下面就是查询操作

由于并不是每个数都恰好是2的k次方

所以只能退而求其次

令k满足2^k<=R-L+1的最大整数

那么

以L开头，以R结尾的两个长度为2^k的区间合起来机覆盖了查询区间[L,R]。

由于是取最小值

所以有些元素

重复考虑了几遍也没关系

（但如果是累加，重复元素就是不允许的了）

原理如下

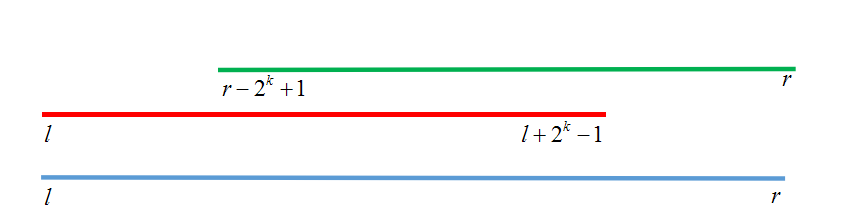
查询的代码：

int RMQ(int L,int R)
{
    int k = ;
    while(<<(k+) <= R-L+)
        k++;//如果2^（k+1）<=R-L+1.那么k还可以加1
        //这步保证k是取了它的最大值，即下面的两个范围是把全部部分都覆盖了
    return min(d[L][k],d[r-(<<k)+][k]);
}

二、二维问题

二维RMQ问题就是求一个矩阵N*M中的一个小块矩阵内的最值问题.其中dmin[i][j][ii][jj]=x表示以(i, j)为左上角,以(i+(1<<ii)-1, j+(1<<jj)-1 )为右下角的矩阵内的最小值.dmax的值类似.

下面dmin[i][j][ii][jj]的值如何求呢?首先我们知道dmin[i][j][0][0]的值就是v[i][j],而假设dmin[i][j][ii][jj]中的ii不为0,那么dmin[i][j][ii][jj]= min(dmin[i][j][ii-1][jj], dmin[i+(1<<ii)][j][ii-1][jj] );如果ii为0,那么就按jj来求.

其实上面的求法就是等于把二维问题转变为一维问题来求解.

下面我们讨论如何查询结果.

对于一个以(x1, y1)为左上角,以(x2, y2)为右下角的矩形,如何求它的最小值和最大值呢?下面假设我们求最小值:

我们把(x1，y1)与(x2，y2)构成的矩形分成四小块，这四小块可能有重合部分，但是它们共同构成了目标矩形：

dmin[x1][y1][ii][jj]

dmin[x1][y2-(1<<jj)+1][ii][jj]

dmin[x2-(1<<ii)+1][y1][ii][jj]

dmin[x2-(1<<ii)+1][y2-(1<<jj)+1][ii][jj]

(自己想象下上面4小块是怎么样的？)

temp 1=min(dmin[x1][y1][ii][jj] , dmin[x1][y2-(1<<jj)+1][ii][jj])

temp 2=min(dmin[x2-(1<<ii)+1][y1][ii][jj] ,dmin[x2-(1<<ii)+1][y2-(1<<jj)+1][ii][jj] )

最终结果是min(temp1, temp2);

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=+;

int dmax[MAXN][];
int dmin[MAXN][];

void initmax(int n,int d[])//初始化最大值查询
{
    for(int i=; i<=n; i++)
        dmax[i][]=d[i];
    for(int j= ; (<<j)<=n ; j++)
        for(int i=; i+(<<j)- <=n; i++)
            dmax[i][j]=max(dmax[i][j-],dmax[i+(<<(j-))][j-]);
}
int getmax(int L,int R)//查询最大值
{
    int k=;
    while((<<(k+))<=R-L+)k++;
    return max(dmax[L][k] , dmax[R-(<<k)+][k]);
}

void initmin(int n,int d[])//初始化最小值查询
{
{
    for(int i=; i<=n; i++)
        dmin[i][]=d[i];
    for(int j=; (<<j)<=n; j++)
        for(int i=;i+(<<j)-<=n;i++)
            dmin[i][j]= min( dmin[i][j-],dmin[i+(<<(j-))][j-] );
}
int getmin(int L,int R)//查询最小值
{
    int k=;
    while( (<<(k+)) <=R-L+)k++;
    return min(dmin[L][k],dmin[R-(<<k)+][k]);
}