matlab-逻辑回归二分类（Logistic Regression）

逻辑回归二分类

今天尝试写了一下逻辑回归分类，把代码分享给大家，至于原理的的话请戳这里 https://blog.csdn.net/laobai1015/article/details/78113214   （在这片博客的基础上我加了一丢丢东西）。

用到的预测函数为

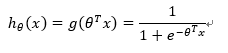
其中，h为预测函数（大于0.5为一类，小于等于0.5为另一类）。θ为各个特征的参数。θ=[θ1,θ2,θ3...]^T

损失函数J(θ)为

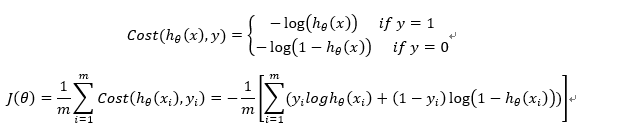
利用梯度下降算法进行参数的更新公式如下：

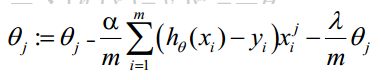
其中，α是学习率参数，λ是正则项参数，需要自己输入。

用上述三个公式即可写出一般情况下的逻辑回归分类，经试验，其分类效果在我的测试数据下有90%以上准确度。

以下代码为了演示方面，只提供了两个特征值，然后加了一个常数项（经过实验，常数项是不可缺少的）。大家在使用自己的数据集的话只需要进行一点小改动即可。

matlab代码如下：

clear
clc

%% 数据准备
%X = xlsread('C:\Users\user01\Desktop\test.xlsx');
%二分类 随机生成数据。  200个数据  每个数据2个特征
data=1*rand(300,2);
label=zeros(300,1);
%label(sqrt(data(:,1).^2+data(:,2).^2)<8)=1;
label((data(:,2)+data(:,1)>1))=1;
%在data上加常数特征项；
data=[data,ones(size(data,1),1)];

%打乱循序
randIndex = randperm(size(data,1));
data_new=data(randIndex,:);
label_new=label(randIndex,:);

%80%训练  20%测试
k=0.8*size(data,1);
X1=data_new(1:k,:);
Y1=label_new(1:k,:);
X2=data_new(k+1:end,:);
Y2=label_new(k+1:end,:);

[m1,n1] = size(X1);
[m2,n2] = size(X2);
Features=size(data,2); %特征个数
 %% 开始训练
%设定学习率为0.01
delta=1;
lamda=0.2; %正则项系数

theta1=rand(1,Features);
%theta1=[.5,.5];
%%训练模型

%梯度下降算法求解theta（每次都是对全部的数据进行训练）
num = 300; %最大迭代次数
L=[];
while(num)
    dt=zeros(1,Features);
    loss=0;
    for i=1:m1
        xx=X1(i,1:Features);
        yy=Y1(i,1);
        h=1/(1+exp(-(theta1 * xx')));
        dt=dt+(h-yy) * xx;
        loss=loss+ yy*log(h)+(1-yy)*log(1-h);
    end
    loss=-loss/m1;
    L=[L,loss];

    theta2=theta1 - delta*dt/m1 - lamda*theta1/m1;
    theta1=theta2;
    num = num - 1;

    if loss<0.01
        break;
    end
end
figure
subplot(1,2,1)
plot(L)
title('loss')

subplot(1,2,2)
x=0:0.1:10;
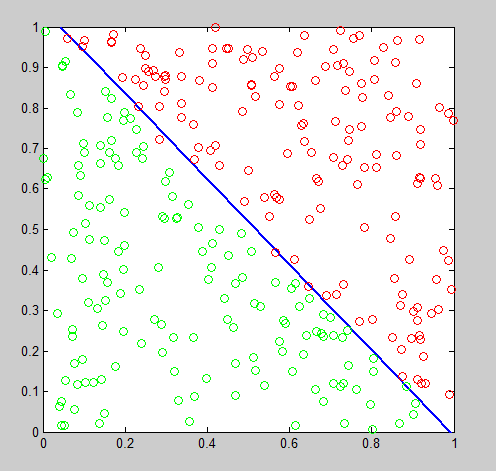
y=(-theta1(1)*x-theta1(3))/theta1(2);
plot(x,y,'linewidth',2)
hold on
plot(data(label==1,1),data(label==1,2),'ro')
hold on
plot(data(label==0,1),data(label==0,2),'go')
axis([0 1 0 1])

%测试数据
acc=0;
for i=1:m2
    xx=X2(i,1:Features)';
    yy=Y2(i);
    finil=1/(1+exp(-theta2 * xx));
    if finil>0.5 && yy==1
        acc=acc+1;
    end
    if finil<=0.5 && yy==0
        acc=acc+1;
    end
end
acc/m2

%测试结果： 测试准确率为95%。

　　

得到的loss曲线为：

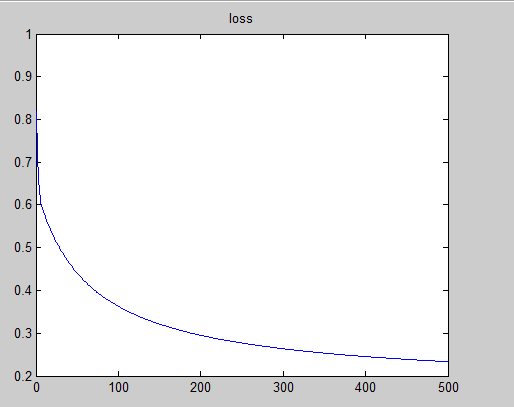
分类图像为：