BZOJ2521:[SHOI2010]最小生成树(最小割)

Description

Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个n个点、m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外，他还知道，某一个图可能有多种不同的最小生成树。例如，下面图 3中所示的都是图 2中的无向图的最小生成树：

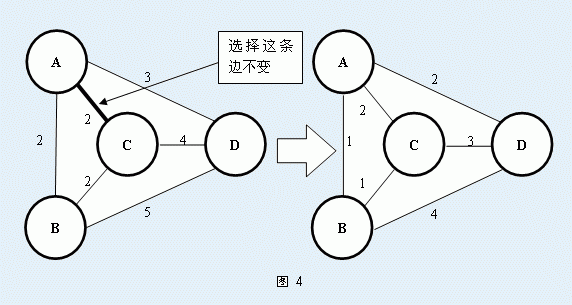
当然啦，这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB，至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中，你可以对这个无向图进行操作，一次单独的操作是指：先选择一条图中的边 P1P2，再把图中除了这条边以外的边，每一条的权值都减少1。如图 4所示就是一次这样的操作：

Input

输入文件的第一行有3个正整数n、m、Lab分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。

接下来m行依次描述标号为1,2,3…m的无向边，每行描述一条边。每个描述包含3个整数x、y、d，表示这条边连接着标号为x、y的点，且这条边的权值为d。

输入文件保证1<=x,y<=N,x不等于y,且输入数据保证这个无向图一定是一个连通图。

Output

输出文件只有一行，这行只有一个整数，即，使得标号为Lab边一定出现最小生成树中的最少操作次数。

Sample Input

4 6 1
1 2 2
1 3 2
1 4 3
2 3 2
2 4 4
3 4 5

Sample Output

1

HINT

第1个样例就是问题描述中的例子。

1<=n<=500,1<=M<=800,1<=D<10^6

Solution

首先题目的操作其实可以看成给一条边权值加一……

首先对于权值比$lab$大的边，我们肯定是不需要管的，因为按照$kruskal$的过程，他们一定在$lab$的后面考虑。

而对于权值比$lab$小的，我们可以通过给他们不停加一使得权值超过$lab$从而靠后考虑。

可以发现，当$(u[lab],v[lab])$这条边会被算到最小生成树里面，只有在权值小于等于它的边加完后，$u[lab]$和$v[lab]$不在一个连通块内。我们把权值小于等于$l[lab]$的图建出来，现在问题变成，你可以用$l[lab]-l[i]+1$的代价砍掉一些边使得$u[lab]$和$v[lab]$不连通，最小割就好了。

Code

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<queue>
 #include<algorithm>
 #define N (1009)
 #define INF (0x7f7f7f7f)
 using namespace std;
 
 struct Edge{int to,next,flow;}edge[N<<];
 int n,m,lab,u[N],v[N],l[N],Depth[N];
 int head[N],num_edge;
 queue<int>q;
 
 inline int read()
 {
     int x=,w=; char c=getchar();
     while (c<'' || c>'') {if (c=='-') w=-; c=getchar();}
     while (c>='' && c<='') x=x*+c-'', c=getchar();
     return x*w;
 }
 
 void add(int u,int v,int l)
 {
     edge[++num_edge].to=v;
     edge[num_edge].next=head[u];
     edge[num_edge].flow=l;
     head[u]=num_edge;
 }
 
 int DFS(int x,int low,int t)
 {
     if (x==t || !low) return low;
     int f=;
     for (int i=head[x]; i; i=edge[i].next)
         if (Depth[edge[i].to]==Depth[x]+)
         {
             int Min=DFS(edge[i].to,min(low,edge[i].flow),t);
             edge[i].flow-=Min;
             edge[((i-)^)+].flow+=Min;
             f+=Min; low-=Min;
             if (!low) break;
         }
     if (!f) Depth[x]=-;
     return f;
 }
 
 bool BFS(int s,int t)
 {
     memset(Depth,,sizeof(Depth));
     Depth[s]=;
     q.push(s);
     while (!q.empty())
     {
         int x=q.front(); q.pop();
         for (int i=head[x]; i; i=edge[i].next)
             if (!Depth[edge[i].to] && edge[i].flow)
             {
                 Depth[edge[i].to]=Depth[x]+;
                 q.push(edge[i].to);
             }
     }
     return Depth[t];
 }
 
 int Dinic(int s,int t)
 {
     int ans=;
     while (BFS(s,t)) ans+=DFS(s,INF,t);
     return ans;
 }
 
 int main()
 {
     n=read(); m=read(); lab=read();
     for (int i=; i<=m; ++i) u[i]=read(),v[i]=read(),l[i]=read();
     for (int i=; i<=m; ++i)
         if (i!=lab && l[i]<=l[lab])
         {
             add(u[i],v[i],l[lab]-l[i]+);
             add(v[i],u[i],l[lab]-l[i]+);
         }
     printf("%d\n",Dinic(u[lab],v[lab]));
 }