LeetCode（78）：子集

Medium！

题目描述：

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

解题思路：

这道求子集合的问题，由于其要列出所有结果，按照以往的经验，肯定是要用递归来做。这道题其实它的非递归解法相对来说更简单一点，下面我们先来看非递归的解法，由于题目要求子集合中数字的顺序是非降序排列的，所有我们需要预处理，先给输入数组排序，然后再进一步处理，最开始是想按照子集的长度由少到多全部写出来，比如子集长度为0的就是空集，空集是任何集合的子集，满足条件，直接加入。下面长度为1的子集，直接一个循环加入所有数字，子集长度为2的话可以用两个循环，但是这种想法到后面就行不通了，因为循环的个数不能无限的增长，所以我们必须换一种思路。

我们可以一位一位的往上叠加，比如对于题目中给的例子[1,2,3]来说，最开始是空集，那么我们现在要处理1，就在空集上加1，为[1]，现在我们有两个自己[]和[1]，下面我们来处理2，我们在之前的子集基础上，每个都加个2，可以分别得到[2]，[1, 2]，那么现在所有的子集合为[], [1], [2], [1, 2]，同理处理3的情况可得[3], [1, 3], [2, 3], [1, 2, 3], 再加上之前的子集就是所有的子集合了。

C++解法一：

 // Non-recursion
 class Solution {
 public:
     vector<vector<int> > subsets(vector<int> &S) {
         vector<vector<int> > res();
         sort(S.begin(), S.end());
         for (int i = ; i < S.size(); ++i) {
             int size = res.size();
             for (int j = ; j < size; ++j) {
                 res.push_back(res[j]);
                 res.back().push_back(S[i]);
             }
         }
         return res;
     }
 };

整个添加的顺序为：

[]
[1]
[2]
[1 2]
[3]
[1 3]
[2 3]
[1 2 3]

下面来看递归的解法，相当于一种深度优先搜索，参见http://www.cnblogs.com/TenosDoIt/p/3451902.html，由于原集合每一个数字只有两种状态，要么存在，要么不存在，那么在构造子集时就有选择和不选择两种情况，所以可以构造一棵二叉树，左子树表示选择该层处理的节点，右子树表示不选择，最终的叶节点就是所有子集合，树的结构如下：

[]
                   /          \
                  /            \
                 /              \
              []                []
           /       \           /    \
          /         \         /      \
       [ ]       []       []     []
      /     \     /   \     /   \    / \
  [  ] [ ] [ ] [] [ ] [] [] []

C++解法二：

 // Recursion
 class Solution {
 public:
     vector<vector<int> > subsets(vector<int> &S) {
         vector<vector<int> > res;
         vector<int> out;
         sort(S.begin(), S.end());
         getSubsets(S, , out, res);
         return res;
     }
     void getSubsets(vector<int> &S, int pos, vector<int> &out, vector<vector<int> > &res) {
         res.push_back(out);
         for (int i = pos; i < S.size(); ++i) {
             out.push_back(S[i]);
             getSubsets(S, i + , out, res);
             out.pop_back();
         }
     }
 };

整个添加的顺序为：

[]
[1]
[1 2]
[1 2 3]
[1 3]
[2]
[2 3]
[3]

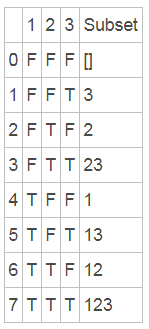
最后我们再来看一种解法，这种解法是CareerCup书上给的一种解法，想法也比较巧妙，把数组中所有的数分配一个状态，true表示这个数在子集中出现，false表示在子集中不出现，那么对于一个长度为n的数组，每个数字都有出现与不出现两种情况，所以共有2ⁿ中情况，那么我们把每种情况都转换出来就是子集了，我们还是用题目中的例子， [1 2 3]这个数组共有8个子集，每个子集的序号的二进制表示，把是1的位对应原数组中的数字取出来就是一个子集，八种情况都取出来就是所有的子集了。

C++解法三：

 class Solution {
 public:
     vector<vector<int> > subsets(vector<int> &S) {
         vector<vector<int> > res;
         sort(S.begin(), S.end());
         int max =  << S.size();
         for (int k = ; k < max; ++k) {
             vector<int> out = convertIntToSet(S, k);
             res.push_back(out);
         }
         return res;
     }
     vector<int> convertIntToSet(vector<int> &S, int k) {
         vector<int> sub;
         int idx = ;
         for (int i = k; i > ; i >>= ) {
             if ((i & ) == ) {
                 sub.push_back(S[idx]);
             }
             ++idx;
         }
         return sub;
     }
 };