程序员的进阶课-架构师之路（13）-B-树

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_37609579/article/details/99699744

一、什么是B-树（B-Tree）

B树是平衡多叉树，可以看做是对2-3树的一种扩展，即允许每个节点有最多M个子节点，其中M为B树的阶。每个节点的多个key按升序排列，且有 节点所含key值的个数 = 节点的子树的个数 – 1，就意味着某节点的每个子树所在的位置是由该节点的key值的分布决定的。B树的另外一个特性就是所有的叶子节点都处于同一层，也就是说从根节点到任意节点的深度都相等（平衡）。

2-3树和2-3-4树都是B树的特例。结点最大的孩子数目称为B树的阶，因此2-3树是3阶B树，2-3-4树是4阶B树。 
B+树是B树的一种变形，二者的差异在于，非叶子节点的节点（就是中间节点）的子树的个数 = 该节点的key的个数，这是因为B+树中的中间节点的key并不用于保存数据，而只用来索引，而叶子节点中包含了全部的key以及value；所有的中间节点的key都同时存在于子节点，且在子节点的key中是最大或者最小的；所有的子节点都按照升序以指针连接在一起。由于B+树的中间节点不再存储value，那么同样大小的磁盘页可以容纳更多的节点元素，因此数据量相同的B树与B+树相比，后者更加“矮胖”，从而可以减少磁盘I/O。B+树因为每次都要查找到叶子节点，因此查找性能稳定。范围查询时只需在叶子节点顺序遍历，更简单。

二、B-树的定义

B-树是一种多路搜索树，要注意，并不是二叉树。

1. 定义任意非叶子结点最多只有M个儿子；且M>2；
2. 根结点的儿子数为[2, M]；
3. 除根结点以外的非叶子结点的儿子数为[M/2, M]；
4. 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
5. 非叶子结点的关键字个数=指向儿子的指针个数-1；
6. 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
7. 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
8. 所有叶子结点位于同一层，且不带任何信息，也是为了保持算法的一致性。

举个栗子：M=3的情况下，我们的B-树是长这样子的：

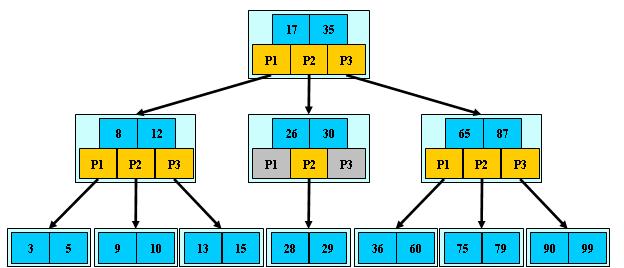
三、B-树的特性

1. 关键字集合分布在整颗树中；
2. 任何一个关键字出现且只出现在一个结点中；
3. 搜索有可能在非叶子结点结束；
4. 其搜索性能等价于在关键字全集内做一次二分查找；
5. 自动层次控制；

四、对B-树的操作

1.B-树插入

一个原始的B-树阶为3，如下图：

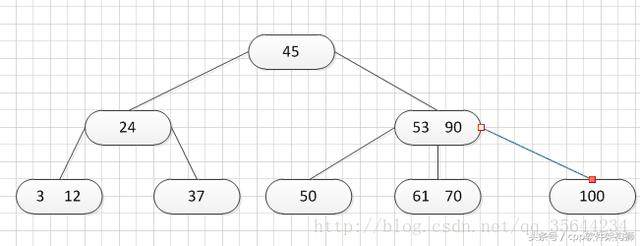
首先，我需要插入一个关键字：30，可以得到如下的结果：

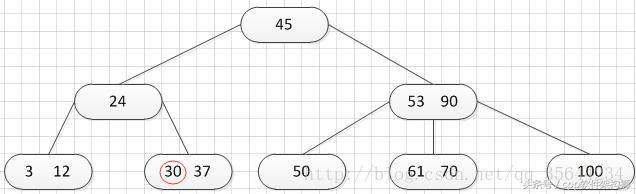
再插入26，得到如下的结果：

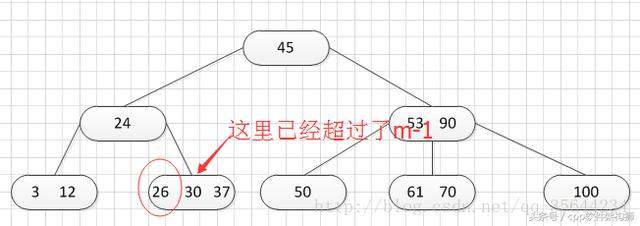
OK，此时如图所示，在插入的那个终端结点中，它的关键字数已经超过了m-1=2，所以我们需要对结点进分裂，所以我们先对关键字排序，得到：26 30 37 ，所以它的左部分为（不包括中间值）：26，中间值为：30，右部为：37，左部放在原来的结点，右部放入新的结点，而中间值则插入到父结点，并且父结点会产生一个新的指针，指向新的结点的位置，如下图所示：

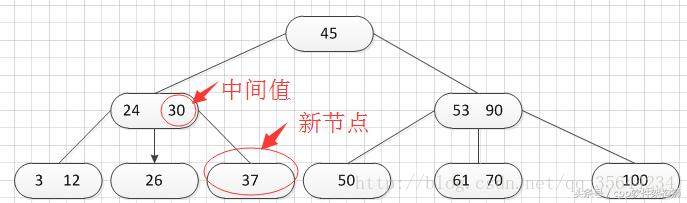
然后我们继续插入新的关键字：85，得到如下图结果：

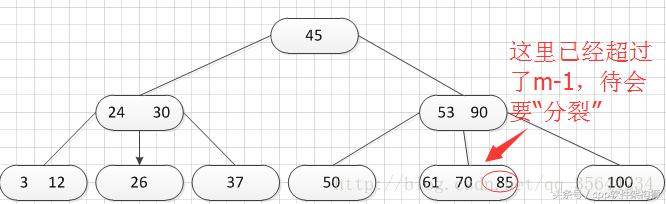
正如图所示，我需要对刚才插入的那个结点进行“分裂”操作，操作方式和之前的一样，得到的结果如下：

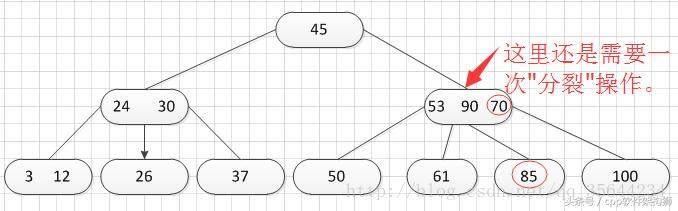
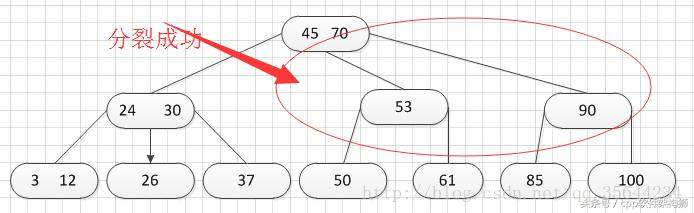
当我们分裂完后，突然发现之前的那个结点的父亲结点的度为4了，说明它的关键字数超过了m-1，所以需要对其父结点进行“分裂”操作，得到如下的结果：

2.B-树删除

待补充（貌似小伙伴们不太喜欢看这个东东）

五、用途

B-树主要应用在文件系统

为了将大型数据库文件存储在硬盘上 以减少访问硬盘次数为目的 在此提出了一种平衡多路查找树——B-树结构。由其性能分析可知它的检索效率是相当高的 为了提高 B-树性能’还有很多种B-树的变型，力图对B-树进行改进。

未完待续。。。

---

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1. https://blog.csdn.net/MustangJy/article/details/87783323
2. https://blog.csdn.net/yishizuofei/article/details/81660841
3. https://www.cnblogs.com/shixiangwan/p/7530015.html
4. https://q.115.com/182920/T1267386.html?uid=20069