DataStructure之线性表以及其实现

线性表

应用：多项式的表示

什么是线性表

多项式表示问题给出的启示：

　　同一个问题可以有不同的表示（存储）方法

　　有一类共性问题 ： 有序线性序列的租住和管理

“线性表（Linear List）” : 由同类型数据元素构成有序序列的线性结构

　　表中元素个数称为线性表的长度

　　线性表没有元素时，称为空表

　　表起始位置称为表头，表结束位置称为表尾

线性表的抽象数据类型描述

类型名称 ： 线性表（List）

数据对象集： 线性表是 n(>=0) 个元素构成的有序序列（a_1, a_2, a_3, ...., a_n）

操作集： 线性表L属于List, 整数i表示位置， 元素X属于ElementType

线性表基本操作主要有：

　　List MakeEmpty(): 初始化一个空性表L；

　　ElementType FindKth(int K, List L）: 根据位序K， 返回相应元素；

　　int Find(ElementType X, List L) : 在线性表L中查找X的第一次出现位置；

　　void Insert(ElementType X, int i, List L): 在位序i前插入一个新元素X；

　　void Delete(int i, List L) ： 删除指定位序i的元素；

　　int Length(List L) : 返回线性表L的长度n;

线性表的顺序存储实现

　　利用数组的连续存储空间顺序存放线性表的各元素

#define MAXSIZE    <............>

typedef struct LNode  *List;

struct LNode{

　　ElementType Data[MAXSIZE];

　　int Last;

};

struct LNode L;

List PtrL;

　　访问下标为i的元素：L.Data[i] 或 PtrL->Data[i]

　　线性表的长度: L.Last+1 或PtrL->Last+1

主要操作的实现

初始化（建立空的顺序表）

List MakeEmpty()

{

　　List PtrL;

　　PtrL = ( List )malloc( sizeof( struct LNode ) );

　　PtrL->Last = -1;

　　return PtrL;

}

查找

int Find(ElementType K, List PtrL)

{

　　int i = 0;

　　while( i <= PtrL->Last && PtrL->Data[i] != X)

　　　　i++;

　　if( i > PtrL->Last) return -1; //如果没有找到， 返回-1

　　else return i;//找到后返回的是存储位置

}

插入（第 i （1 <= i <= n+1）个位置上插入一个值为X的新元素）

这里的要注意的是， 这里的代码是采用的从1开始计数的设计

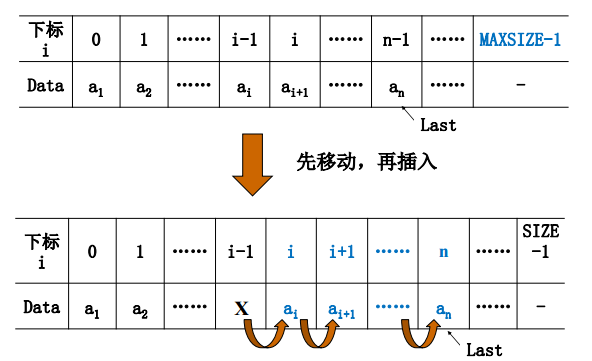
插入操作的具体实现

需要注意这里的是， 这里的位置是从1开始计数（就是人类默认的第一位置的元素就是第一个，对于计算机中来说，还可以有从0开始计数，普遍的来说，在计算机中大都是从0开始计数的）

void Insert ( ElementType X, int  i, List PtrL)

{

　　int j;

　　if ( PtrL->Last == MAXSIZE - 1){ //表的空间已满， 不能插入新的元素（这里的MAXSiZE - 1是能插入进去的最后的一个位置， 而MASIZE代表的是表中元素最多的元素个数）

　　　　printf ( " 表满 ");

　　　　return ;

　　}

　　if ( i < 1 || i > PtrL->Last+2){

/*对于 PtrL->Last 表示的数链表中数组元素的最后一个元素的位置信息（这里的位置信息时采用从0开始计数的），因此要是采用从1开始计数的话，这个位置就是第PtrL->Last + 1 位置上的元素， 但是要插入元素的范围是在(1 <= i <= n+1) 即， 第一位置开始， 到第n + 1位置开始， 因此这里的最后一个位置要插入的位置(第n+1位置）用PtrL->Last表示的话就是PtrL->Last + 2位置，

所以这里判断的i 的范围，就可以很容易的知道这里的范围的含义。*/

　　　　printf ( " 位置不合法 ");

　　　　return;

　　}

　　for ( j = PtrL->Last; i >= i - 1; j--）

　　　　PtrL->Data[j + 1] = PtrL->Data[j];//将a_i .... a_n 倒序向后移动

　　PtrL->Data[i - 1]  = X;//新元素插入

　　PtrL->Last++;//Last仍指向最后元素

　　return;

}

//插入的另一个版本， 这里采用的计数就是在0开始进行计数的

void  Insert(List L, Elementype X, Position P)

{

    /*在L的指定位置P前插入一个新元素X*/

    Position i;

    

    if(L->Last == MAXSIZE -1)

    {

        /*表空间已满，不能插入*/

        printf("表满");

        return FALSE;

    }

　　

    if( P < 0 || P > L->Last + 1){//这里是变化的不同之处，这里的采用的就是从0开始计数判断插入位置的合法性

        //检查插入位置时候合法

        printf("位置不合法");

        return FALSE;

    }

    for( i = L->Last; i >= P; i--)

        L->Data[i+1] = L->Data[i]; //将位置P以及以后位置往后移动

    L->Data[P] = X;//新元素插入

    L->Last++;//Last 仍指向最后一个元素

    return ;

}

删除（删除表的第 i （1 <= i <=n）个位置上的元素）

删除操作的实现 (这里也是有位置计数的为题，下面这个采用的是从第1个位置开始计数的)

void Delete( int i, List PtrL)

{

　　int j;

　　if ( i < 1 || i > PtrL->Last + 1){

　　　　printf ( "不存在第%d个元素", i);

　　　　return;

　　}

　　for ( j = i; j <= PtrL->Last; j++)

　　　　PtrL->Data[j - 1] = PtrL->Data[j];//将a_(i+1) ..... a_n顺序向前移动

　　PtrL->Last--;//Last仍指向最后元素

　　return ;

}

//这里采用的计数位置是从0开始计数的

BOOL Delete(List L, Position P)

{

    //从L 中删除指定位置P的元素

    Position i;

    if ( P < 0 || P > L->Last){

        //检查空表集删除位置的合法性

        printf("位置%d不存在元素",P);

        return FALSE;

    }

    for( i = P + 1; i <= L->Last; i++)

        L->Data[i - 1] = L->Data[i];//将位置P+1及以后的位置往前移

    L->Last--;//last 指向最后一个元素

    return  TRUE;

}

完整测试代码：

/*list_array.c*/

#include <stdio.h>//printf

#include <stdlib.h>//malloc

#define MAXSIZE 2000

#define TRUE 1

#define FALSE 0

#define ERROR -1

typedef int BOOL;

typedef int Elementype;

typedef int Position;

typedef struct LNode* List;

//数组实现链表， 定义的数据结构

struct  LNode{

    Elementype Data[MAXSIZE];

    Position Last;

};

Position Length(List L);

/*init*/

List MakeEmpty()

{

    List L;

    L = (List)malloc(sizeof(struct LNode));

    L->Last = -1;

    return L;

}

/* 查找 */

Position Find(List L, Elementype X)

{

    Position i = 0;

    

    while( i <= L->Last && L->Data[i] != X)

        i++;

    if( i > L->Last){ 

        return ERROR; //如果没有找到，返回错误信息

    }else{

        return i;//找到后返回的是存储位置

    }

}

BOOL Insert(List L, Elementype X, Position P)

{

    /*在L的指定位置P前插入一个新元素X*/

    Position i;

    

    if(L->Last == MAXSIZE -1)

    {

        /*表空间已满，不能插入*/

        printf("表满");

        return FALSE;

    }

    if( P < 0 || P > L->Last + 1){

        //检查插入位置时候合法

        printf("位置不合法");

        return FALSE;

    }

    for( i = L->Last; i >= P; i--)

        L->Data[i+1] = L->Data[i]; //将位置P以及以后位置往后移动

    L->Data[P] = X;//新元素插入

    L->Last++;//Last 仍指向最后一个元素

    return TRUE;

}

BOOL Delete(List L, Position P)

{

    //从L 中删除指定位置P的元素

    Position i;

    if ( P < 0 || P > L->Last){

        //检查空表集删除位置的合法性

        printf("位置%d不存在元素",P);

        return FALSE;

    }

    for( i = P + 1; i <= L->Last; i++)

        L->Data[i - 1] = L->Data[i];//将位置P+1及以后的位置往前移

    L->Last--;//last 指向最后一个元素

    return  TRUE;

}

void PrintList(List L)

{

    Position i;

    for(i = 0; i < Length(L); i++)

        printf("%d ", L->Data[i]);

    printf("\n");

}

Position Length(List L)

{

    return L->Last + 1;

}

Elementype getElement(List L, Position P)

{

    return L->Data[P];

}

int main()

{

    List list;

    list = MakeEmpty();

    Position index = 0;

    for(int i = 10; i >= 0; i--)

    {

        if(Insert(list,i,index)){

            printf("    insert success\n");

        }else{

            printf("    insert failed\n");

        }

        index++;

    }

    PrintList(list);

    printf("this list length : %d\n", Length(list));

    printf("the positon 2 is : %d \n", getElement(list, 10));

    return 0;    

}

编译运行：

　　gcc list_array.c

　　./a.exe

打印结果：

insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
insert success
10 9 8 7 6 5 4 3 2 1 0
this list length : 11
the positon 2 is : 0

——————————————————————————————————线性表的顺序存储———————————————————————————————————