tarjan学习（复习）笔记（持续更新）（各类找环模板）

题目背景

缩点+DP

题目描述

给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入输出格式

输入格式：

第一行，n,m

第二行，n个整数，依次代表点权

第三至m+2行，每行两个整数u,v，表示u->v有一条有向边

输出格式：

共一行，最大的点权之和。

输入输出样例

输入样例#1： 复制

2 2
1 1
1 2
2 1

输出样例#1： 复制

2

说明

n<=10^4,m<=10^5,0<=点权<=1000

算法：Tarjan缩点+DAGdp、

基本可以算是套路了吧，先缩点，然后tpsort，跑dp，是不是可以解决不少图论题目呢

思路：

两个数组，dfn，low。

dfn：dfs序（时间戳）

low：以u为根的子树里dfn最小的那个点（它的最早祖先）

附属数组：

st：模拟栈

co：重建图的联通快（点）

维护这两个数组，当dfn[u]=low[u]时判定为强连通分量（环）

为什么呢？

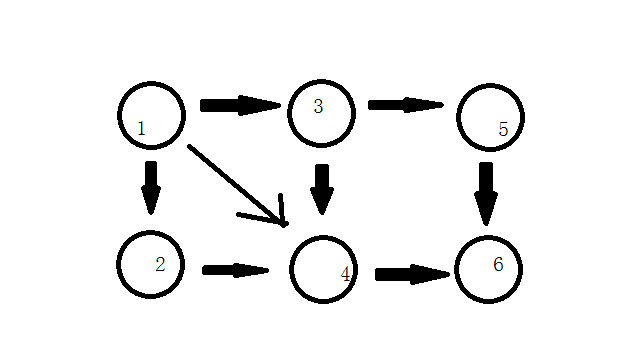
当一个点它的最老祖先等于它自己的时候，这就是一个环啊

了解四种边：

树枝边：遍历路径

前向边：爹——>儿

后向边：儿——>爹

横插边：从这个子树插到另外一个搜索子树的边

下面介绍怎么维护low

如果（u，v）是树枝边，一切好说，直接比较low[u]和low[v]的最小值即可，因为v是u的儿子，直接比较它们最早祖先的大小。

如果（u，v）是后向边或者横插边，就需要比较lou[u]和dfn[v]的最小值。

为什么？

后向边相对好理解，从这个点可以回溯到它的祖先，我们需要比较它儿子们的时间戳最小值和它祖先的时间戳 的最小值。

若之前搜到过u的祖先，那么它祖先的dfn一定是小的，但是我能从它的耳孙之间找到它的身影（自交？回交？）！

这说明什么？强连通分量！

但是，不要着急，我们需要找到强连通分量的根。所以我们需要比较一个极小值。

解释通了，那么横插边也是同理。

当dfn=low时：

也就是说它的子孙的最高祖先就是子孙本身时。

dfn时间戳正好是它子树节点的low的最小值。因为dfn值具有不重复性，所以可以断定，以它为根的子树的所有点都是一个强连通分量。

所以，可以很好地判断图的环。

注意：因为图可能不连通，所以要多次跑tarjan。

时间复杂度：由于每个点只遍历了一次，每条边也只遍历了一次，所以O(N+M)（不是spfa那么不靠谱，人家就是N+M）

给出缩点板子的代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
struct node
{
    int next,to;
}e[maxn];
int head[maxn],cnt,sum[maxn],a[maxn];
int n,m,ru[maxn];
inline void addedge(int from,int to)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    head[from]=cnt;
}
int dep,top;
int dfn[maxn],low[maxn],vis[maxn],co[maxn],st[maxn];
void tarjan(int u)
{
    dfn[u]=low[u]=++dep;
    vis[u]=;
    st[++top]=u;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[v],low[u]);
        }
        else if(vis[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u])//退栈，把强连通分量薅出来
    {
        int t;
        do
        {
            t=st[top--];
            sum[u]+=a[t];
            co[t]=u;
            vis[t]=;
        }while(t!=u);
    }
}
int dp[maxn];
queue < int > q;
void tpsort()
{
    for(int i=;i<=n;i++)
    {
        if(ru[i]==&&co[i]==i)
        q.push(i);
        dp[co[i]]=sum[co[i]];
    }
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            dp[v]=max(dp[u]+sum[co[v]],dp[v]);
            if(!(--ru[v]))
            {
                q.push(v);
            }
        }
    }
}

pair < int , int > g[maxn];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    for(int i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        addedge(x,y);
        g[i].first=x;
        g[i].second=y;
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i])
        tarjan(i);
    }
    memset(e,,sizeof(e));
    memset(head,,sizeof(head));
    cnt=;
    for(int i=;i<=m;i++)
    {
        int x=g[i].first;
        int y=g[i].second;
        if(co[x]!=co[y])
        {
            addedge(co[x],co[y]);
            ru[co[y]]++;
        }
    }
    tpsort();
    int ans=-;
    for(int i=;i<=n;i++)
    {
        ans=max(ans,dp[i]);
    }
    printf("%d",ans);
    return ;
}

无向图：

void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    st[++top]=u;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(!vis[i])
        {
            vis[i]=vis[i^]=;
            if(dfn[v]==)
            {
                tarjan(v);
                low[u]=min(low[u],low[v]);
            }
            else
            {
                low[u]=min(low[u],dfn[v]);
            }
        }
    }
    if(dfn[u]==low[u])
    {
        color[u]=++col;
        while(st[top]!=u)
        color[st[top]]=col,top--;
        top--;
    }
}

（完）