数据结构（三十二）图的遍历（DFS、BFS）

　　图的遍历和树的遍历类似。图的遍历是指从图中的某个顶点出发，对图中的所有顶点访问且仅访问一次的过程。通常有两种遍历次序方案：深度优先遍历和广度优先遍历。

　　一、深度优先遍历

　　深度优先遍历（Depth_First_Search），也称为深度优先搜索，简称为DFS。深度优先遍历类似于树的前序遍历。

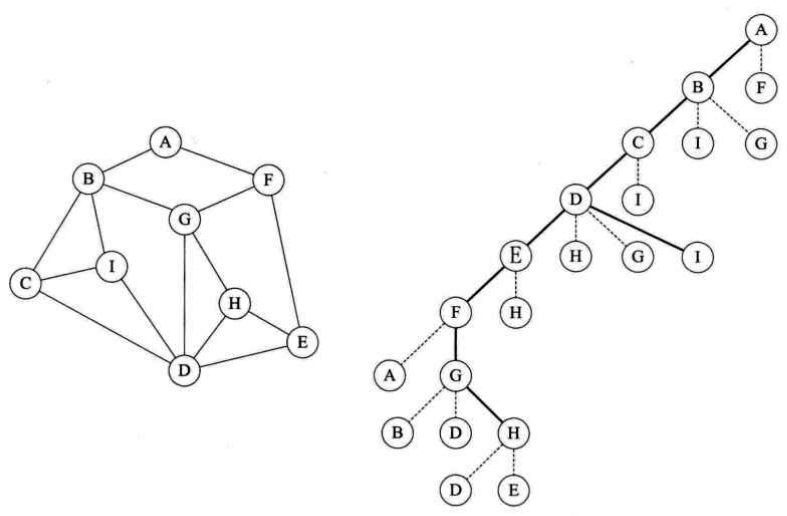
　　DFS算法描述：从图的某个顶点v开始访问，然后访问它的任意一个邻接点w1,；再从w1出发，访问与w1邻接但未被访问过的顶点w2；然后从w2出发，进行类似访问，如此进行下去，直至所有邻接点都被访问过为止。接着，退回一步，退回到前一次刚访问过的顶点，看是否还有其他未被访问过的邻接点。如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问。重复上述过程，直到连通图中所有顶点都被访问过为止。

　　二、广度优先遍历

　　广度优先遍历（Breadth_First_Search），又称为广度优先搜索，简称BFS。图的广度优先遍历类似于树的层序遍历。

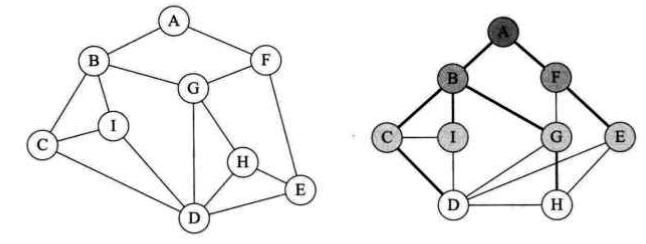
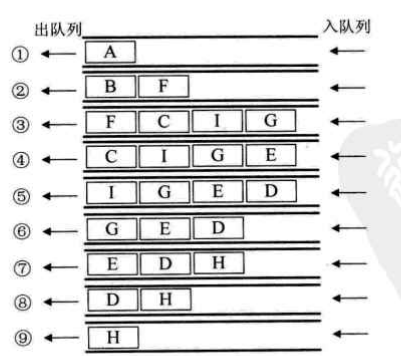
　　BFS算法描述：从图中的某个顶点v开始，先访问该顶点，再依次访问该顶点的每一个未被访问过的邻接点w1，w2，...；然后按此顺序访问顶点w1，w2...的各个还未 被访问过的邻接点。重复上述过程，直到图中的所有顶点都被访问过为止。

　　以下面的例子为例，深度优先遍历的顶点访问序列为：{A B C D E F G H I}；广度优先遍历的顶点访问序列为：{A B F C I G E D H}

　　

　　

　　三、图的遍历算法实现

　　1.深度优先遍历

　　（1）C语言实现

/* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph G, int i)
{
    int j;
     visited[i] = TRUE;
     printf("%c ", G.vexs[i]);/* 打印顶点，也可以其它操作 */
    for(j = ; j < G.numVertexes; j++)
        if(G.arc[i][j] ==  && !visited[j])
             DFS(G, j);/* 对为访问的邻接顶点递归调用 */
}

/* 邻接矩阵的深度遍历操作 */
void DFSTraverse(MGraph G)
{
    int i;
     for(i = ; i < G.numVertexes; i++)
         visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
    for(i = ; i < G.numVertexes; i++)
         if(!visited[i]) /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */
            DFS(G, i);
}

　　（2）Java语言实现

package bigjun.iplab.adjacencyMatrix;

public class Depth_First_Search {

    private static boolean[] visited;                // 访问标识数组

    public static void DFSTraverse(AdjacencyMatrixGraphINF G) throws Exception{
        System.out.print("图的深度优先遍历序列为: ");
        visited = new boolean[G.getVexNum()];
        for (int v = 0; v < G.getVexNum(); v++)     // 访问标志数组初始化都为false，即未访问过
            visited[v] = false;
        for (int v = 0; v < G.getVexNum(); v++)     // 如果没有访问过就对顶点调用深度优先遍历算法
            if (!visited[v])
                DFS(G, v);
        System.out.println();
    }

    private static void DFS(AdjacencyMatrixGraphINF G, int v) throws Exception {
        visited[v] = true;                            // 先将访问标识数组置为true
        System.out.print(G.getVex(v).toString() + " ");
        for (int w = G.firstAdjvex(v); w >= 0; w = G.nextAdjvex(v, w))
            if (!visited[w])
                DFS(G, w);
    }

}

　　2.广度优先遍历

　　（1）C语言实现

Boolean visited[MAXSIZE]; /* 访问标志的数组 */

/* 邻接表的深度优先递归算法 */
void DFS(GraphAdjList GL, int i)
{
    EdgeNode *p;
     visited[i] = TRUE;
     printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */
    p = GL->adjList[i].firstedge;
    while(p)
    {
         if(!visited[p->adjvex])
             DFS(GL, p->adjvex);/* 对为访问的邻接顶点递归调用 */
        p = p->next;
     }
}

/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphAdjList GL)
{
    int i;
     for(i = ; i < GL->numVertexes; i++)
         visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
    for(i = ; i < GL->numVertexes; i++)
         if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */
            DFS(GL, i);
}

　　（2）Java语言实现

package bigjun.iplab.adjacencyMatrix;

import bigjun.iplab.linkQueue.LinkQueue;

public class Breadth_First_Search {

    private static boolean[] visited;

    public static void BFSTraverse(AdjacencyMatrixGraphINF G) throws Exception{
        System.out.print("图的广度优先遍历序列为: ");
        visited = new boolean[G.getVexNum()];
        for (int v = 0; v < G.getVexNum(); v++)             // 访问标志数组初始化都为false，即未访问过
            visited[v] = false;
        for (int v = 0; v < G.getVexNum(); v++)             // 如果没有访问过就对顶点调用深度优先遍历算法
            if (!visited[v])
                BFS(G, v);
        System.out.println();
    }

    private static void BFS(AdjacencyMatrixGraphINF G, int v) throws Exception {
        visited[v] = true;                                    // 先将访问标识数组置为true
        System.out.print(G.getVex(v).toString() + " ");        // 然后访问对应数组下标的顶点
        LinkQueue queue = new LinkQueue();                    // 链队列初始化
        queue.queueEnter(v);                                // 将访问过的顶点的数组下标入队列
        while (!queue.isqueueEmpty()) {
            int u = (Integer) queue.queuePoll();            // 队列队头元素出队列并赋值给u
            for (int w = G.firstAdjvex(u); w >= 0; w = G.nextAdjvex(u, w)) {
                if (!visited[w]) {
                    visited[w] = true;
                    System.out.print(G.getVex(w).toString() + " ");
                    queue.queueEnter(w);
                }
            }
        }
    }

}

　　四、（举例）邻接矩阵的深度优先遍历和广度优先遍历

    // 手动创建一个无向图
    public static AdjacencyMatrixGraphINF createUDGByYourHand() {
        Object vexs_UDG[] = {"A", "B", "C", "D", "E", "F", "G", "H", "I"};
        int[][] arcs_UDG = new int[vexs_UDG.length][vexs_UDG.length];
        for (int i = 0; i < vexs_UDG.length; i++)         // 构造无向图邻接矩阵
            for (int j = 0; j < vexs_UDG.length; j++)
                arcs_UDG[i][j] = 0;
        arcs_UDG[0][1] = 1;
        arcs_UDG[0][5] = 1;
        arcs_UDG[1][2] = 1;
        arcs_UDG[1][6] = 1;
        arcs_UDG[1][8] = 1;
        arcs_UDG[2][3] = 1;
        arcs_UDG[2][8] = 1;
        arcs_UDG[3][4] = 1;
        arcs_UDG[3][6] = 1;
        arcs_UDG[3][7] = 1;
        arcs_UDG[3][8] = 1;
        arcs_UDG[4][5] = 1;
        arcs_UDG[4][7] = 1;
        arcs_UDG[5][6] = 1;
        for (int i = 0; i < vexs_UDG.length; i++)         // 构造无向图邻接矩阵
            for (int j = i; j < vexs_UDG.length; j++)
                arcs_UDG[j][i] = arcs_UDG[i][j];
        return new AdjMatGraph(GraphKind.UDG, vexs_UDG.length, 14, vexs_UDG, arcs_UDG);
    }

    public static void main(String[] args) throws Exception {
        AdjMatGraph DNG_Graph = (AdjMatGraph) createUDGByYourHand();
        Depth_First_Search.DFSTraverse(DNG_Graph);
        Breadth_First_Search.BFSTraverse(DNG_Graph);
    }

输出为：
图的深度优先遍历序列为: A B C D E F G H I
图的广度优先遍历序列为: A B F C G I E D H 

　　五、（举例）邻接表的深度优先遍历和广度优先遍历

    public static void main(String[] args) throws Exception {
        AdjListGraph aListGraph = new AdjListGraph();
        aListGraph.createGraph();
        System.out.println("该类型的图已经创建完成！");
        System.out.println("顶点数组下标为2的第一个邻接点的数组下标是: " + aListGraph.firstAdjvex(2));
        int numOfV2 = aListGraph.firstAdjvex(2);
        System.out.println("顶点V2的第一个邻接点是: " + aListGraph.getVex(numOfV2));
        System.out.println("顶点数组下标为2的相对于顶点数组下标为0的下一个邻接点的数组下标是: " + aListGraph.nextAdjvex(2, 0));
        int numOfV2toV0next = aListGraph.nextAdjvex(2, 0);
        System.out.println("顶点V2相对于V0的邻接点是: " + aListGraph.getVex(numOfV2toV0next));
        Depth_First_Search.DFSTraverse(aListGraph);
        Breadth_First_Search.BFSTraverse(aListGraph);
    }

输出为：
请输入图的类型代号(UDG(无向图)、DG(有向图)、UDN(无向网)、DN(有向网)):
UDG
请分别输入图的顶点数，图的边数:
5 6
请分别输入图的各个顶点:
V0 V1 V2 V3 V4
请输入各个边的两个顶点(第一个输入是弧尾，第二个输入是弧头):
V0 V4
V1 V2
V1 V0
V2 V3
V2 V0
V3 V4
该类型的图已经创建完成！
顶点数组下标为2的第一个邻接点的数组下标是: 0
顶点V2的第一个邻接点是: V0
顶点数组下标为2的相对于顶点数组下标为0的下一个邻接点的数组下标是: 3
顶点V2相对于V0的邻接点是: V3
图的深度优先遍历序列为: V0 V2 V3 V4 V1
图的广度优先遍历序列为: V0 V2 V1 V4 V3