MIT线性代数：7.主变量，特解，求解AX=0的更多相关文章

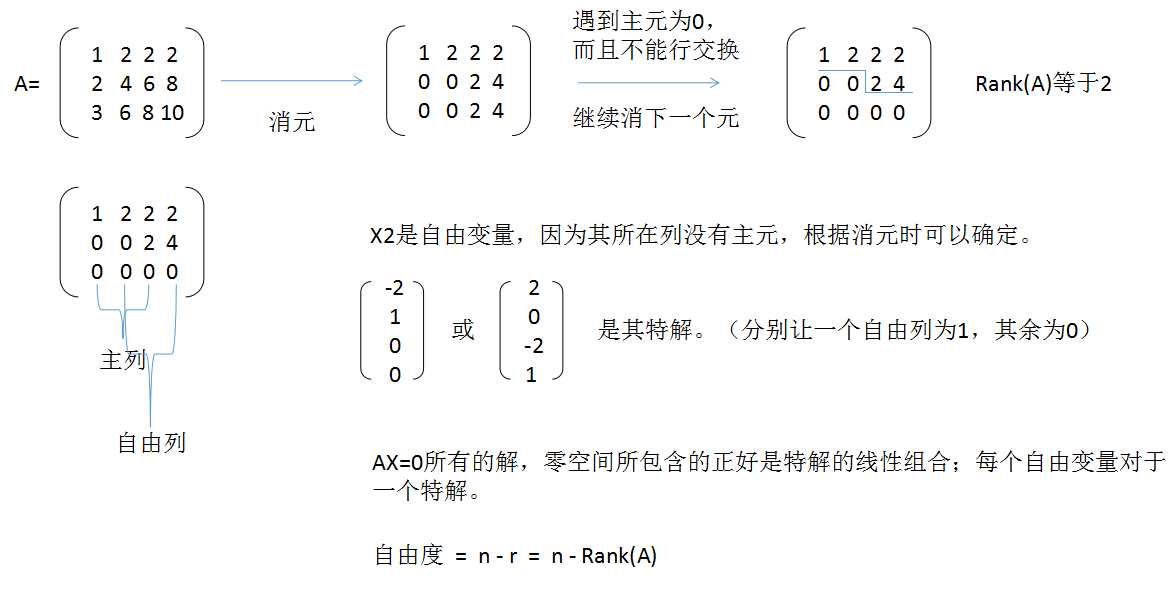
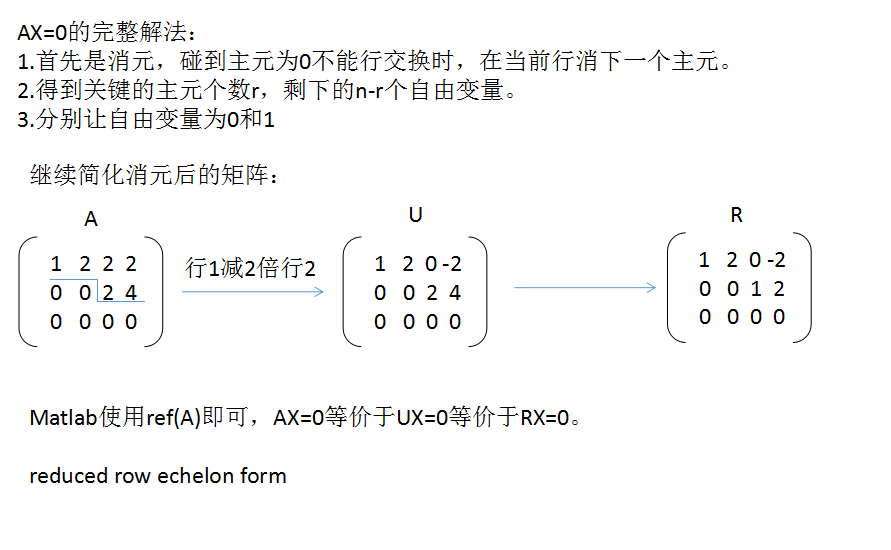
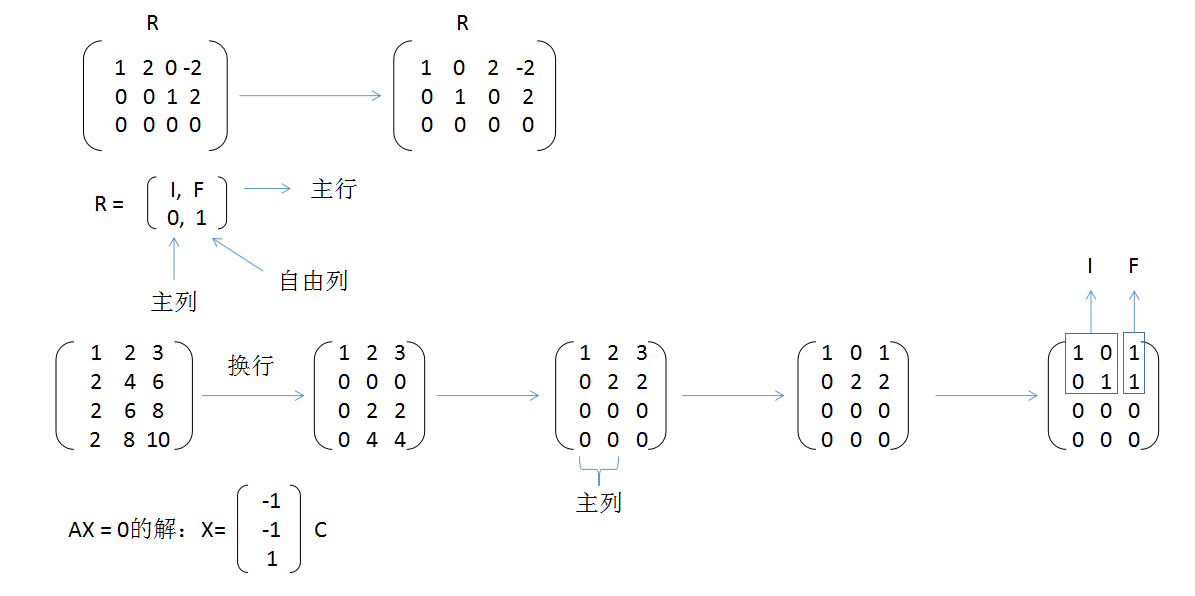
  1. 07-求解Ax=0：主变量、特解

    一.定义转向算法 在第六节讲了空间,列空间,零空间的定义,这节主要讲解如何求出这些空间,即求解$Ax=0$的过程是怎么样的过程,以下面的矩阵$A$为例:(这里主要是长方阵) $A=\left[\beg ...

  2. 求解Ax=b

    一 线性方程组 Ax=b 的解释 线性方程组 Ax=b,其中矩阵 A 尺寸为 m*n, 当 A 为方正时,可使用消元法判断解是否存在并求解.当 A 为长方形矩阵时,同样可使用消元法判断解存在情况并求解 ...

  3. MIT线性代数课程 总结与理解-第一部分

    概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...

  4. phpinfo() 中 Local Value（局部变量）Master Value（主变量） 的区别

    [题外话]phpinfo()这个函数可以查看很多php的信息,要 记得使用 phpinfo() 的很多部分有两个Column:Local Value(局部变量)和 Master Value(主变量) ...

  5. 【读书笔记】：MIT线性代数(5):Four fundamental subspaces

    At the beginning, the difference between rank and dimension: rank is a property for matrix, while di ...

  6. 【读书笔记】：MIT线性代数(3):Special Solution, Rank and RREF

    Special Solutions: Notice what is special about s 1 and S2. They have ones and zeros in the last two ...

  7. 【读书笔记】：MIT线性代数(2):Vector Spaces and Subspaces

    Vector Space: R1, R2, R3,R4 , .... Each space Rn consists of a whole collection of vectors. R5 conta ...

  8. 错误: 找不到或无法加载主类 Files\apache-activemq-5.10.0\bin\..\conf\login.config

    在启动activemq的时候出现错误:“错误: 找不到或无法加载主类 Files\apache-activemq-5.10.0\bin\..\conf\login.config”,之前用activem ...

  9. javascript中判断变量时变量值为 0 的特殊情况

    有时候我们在js中会直接判断变量是否存在值,下面列举一些情况: var a = 0; var b = 1; var c = ' '; var d; console.log( a ? 1 : null) ...

随机推荐

  1. ping本地局域网

    #!/bin/bash for i in `seq 1 254` do ping -c 1 192.168.192.$i > /dev/null if [ $? -eq 0 ];then ech ...

  2. 基于SpringBoot+WebSocket搭建一个简单的多人聊天系统

    前言   今天闲来无事,就来了解一下WebSocket协议.来简单了解一下吧. WebSocket是什么   首先了解一下WebSocket是什么?WebSocket是一种在单个TCP连接上进行全双工 ...

  3. 【mybatis】1mybatis下载、配置与初步使用

    一.mybatis历史: 额,学习一门新事物时了解一下它的历史能在脑中形成一个大致的轮廓...进入正题... mybatis以前叫做ibatis,ibatis是Apache旗下的产品,在2010年时g ...

  4. Spring Boot 2.X(一)：入门篇

    什么是 Spring Boot Spring Boot 是由 Pivotal 团队提供的全新框架,其设计目的是用来简化新 Spring 应用的初始搭建以及开发过程.该框架遵循"约定优于配置& ...

  5. docker升级后启动报错400 Client Error: Bad Request ("Unknown runtime specified docker-runc")

    宝塔面板docker升级后启动容器时报错400 Client Error: Bad Request ("Unknown runtime specified docker-runc" ...

  6. 同步与互斥_percpu变量

    percpu变量的关键就是:要求根据CPU的个数,在内存中生成多份拷贝,并且能够根据变量名和CPU编号,正确的对各个CPU的变量进行寻址. 采用per-cpu变量有下列好处:所需数据很可能存在于处理器 ...

  7. 爬虫破解知乎登入(不使用Selenium模块)

    一.分析 知乎完成登入的步骤 首先获得cookies(如果不获得后面验证码无法获得) 获得验证码 提交登入相关内容 前两步简单稍微细心寻找规律即可 其中最难的是第三步应该他前端进行了js加密 这里没什 ...

  8. VMware15.5版本下安装CentOS_7_64bit

    本文介绍在VMware15.5版本下安装CentOS7. 工具准备: 1.VMware15.5版本 2.CentOS 7 64bit ISO镜像文件 一.创建虚拟机 这部分请参照我的另一个博客“一.新 ...

  9. Jenkins源代码管理（SVN）

    Subversion 安装插件 1.首先将本地的自动化用例打包上传svn 2.配置jenkins源代码管理(每次执行jenkins时,会自动check-out配置地址中的代码到Jenkins的工作空间 ...

  10. Jenkins部署（基于windows）

    一.安装jdk,配置环境变量 二.安装tomcat和jenkins 1.检查电脑上8080端口是否被占用: 命令行中输入:netstat -ano 2.下载Tomcat Tomcat官方网站:http ...