Spring 2017 Assignments2
一.作业要求
原版:http://cs231n.github.io/assignments2017/assignment2/
翻译:http://www.mooc.ai/course/268/learn?lessonid=2029#lesson/2029
二.作业收获及代码
完整代码地址:https://github.com/coldyan123/Assignment2
1 全连接网络
使用一种更模块化的方法,实现了线性层,Relu层,softmax层的前向和反向传播,然后使用for循环就可以实现任意层数的全连接Relu网络。并且还实现了sgd,带动量sgd,RMSProp,Adam几种优化方法和对比。这一部分很简单。
2 Batch Normalization
实现了BN层的前向传播和反向传播,关键代码为:
BN前向传播:
def batchnorm_forward(x, gamma, beta, bn_param):
"""
Forward pass for batch normalization. During training the sample mean and (uncorrected) sample variance are
computed from minibatch statistics and used to normalize the incoming data.
During training we also keep an exponentially decaying running mean of the
mean and variance of each feature, and these averages are used to normalize
data at test-time. At each timestep we update the running averages for mean and variance using
an exponential decay based on the momentum parameter: running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var Note that the batch normalization paper suggests a different test-time
behavior: they compute sample mean and variance for each feature using a
large number of training images rather than using a running average. For
this implementation we have chosen to use running averages instead since
they do not require an additional estimation step; the torch7
implementation of batch normalization also uses running averages. Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9) N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype)) out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# #
# You should store the output in the variable out. Any intermediates #
# that you need for the backward pass should be stored in the cache #
# variable. #
# #
# You should also use your computed sample mean and variance together #
# with the momentum variable to update the running mean and running #
# variance, storing your result in the running_mean and running_var #
# variables. #
#######################################################################
sample_mean = np.mean(x, axis=0)
sample_var = np.mean(x ** 2, axis=0) - sample_mean ** 2
normal_x = (x - sample_mean) / np.sqrt(sample_var + eps)
out = gamma * normal_x + beta
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
cache = (gamma, beta, sample_mean, sample_var, normal_x, eps, x)
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
normal_x = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * normal_x + beta
#######################################################################
# END OF YOUR CODE #
#######################################################################
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode) # Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var return out, cache
BN反向传播(这里没有自己推,直接用的论文里的梯度公式):
def batchnorm_backward(dout, cache):
"""
Backward pass for batch normalization. For this implementation, you should write out a computation graph for
batch normalization on paper and propagate gradients backward through
intermediate nodes. Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward. Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
###########################################################################
gamma, beta, sample_mean, sample_var, normal_x, eps, x = cache
m = x.shape[0]
dnormal_x = dout * gamma
dvar = np.sum(dnormal_x * (x - sample_mean), axis=0) * (-0.5) * (sample_var + eps) ** (-1.5)
dmean = np.sum(-1 / np.sqrt(sample_var + eps) * dnormal_x, axis=0) + dvar * np.sum(-2 * (x - sample_mean), axis=0) / m
dx = 1 / np.sqrt(sample_var + eps) * dnormal_x + dvar * 2 * (x - sample_mean) / m + dmean / m
dgamma = np.sum(dout * normal_x, axis=0)
dbeta = np.sum(dout, axis=0)
###########################################################################
# END OF YOUR CODE #
########################################################################### return dx, dgamma, dbeta
之后,将BN层加入到深度网络中进行实验:
(1)实验1比较了使用和不使用BN的网络,发现使用BN之后收敛速度更快:
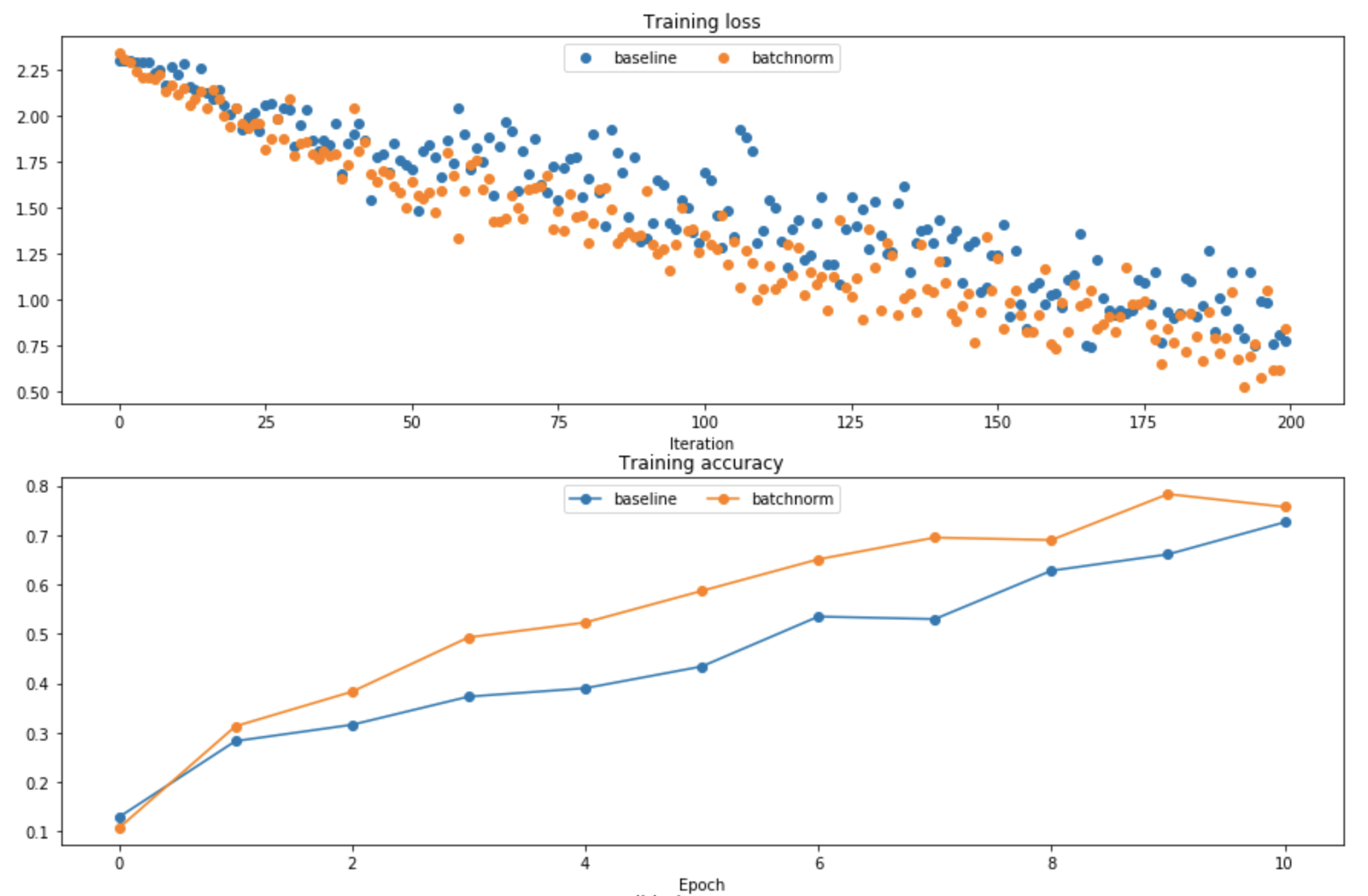
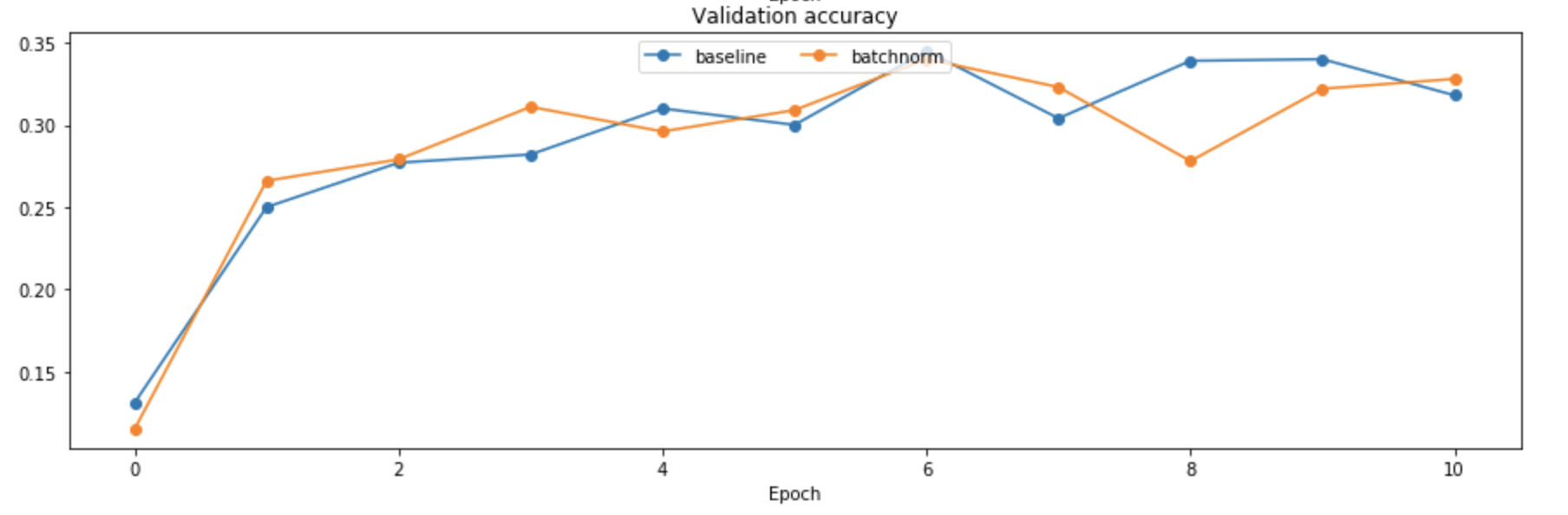
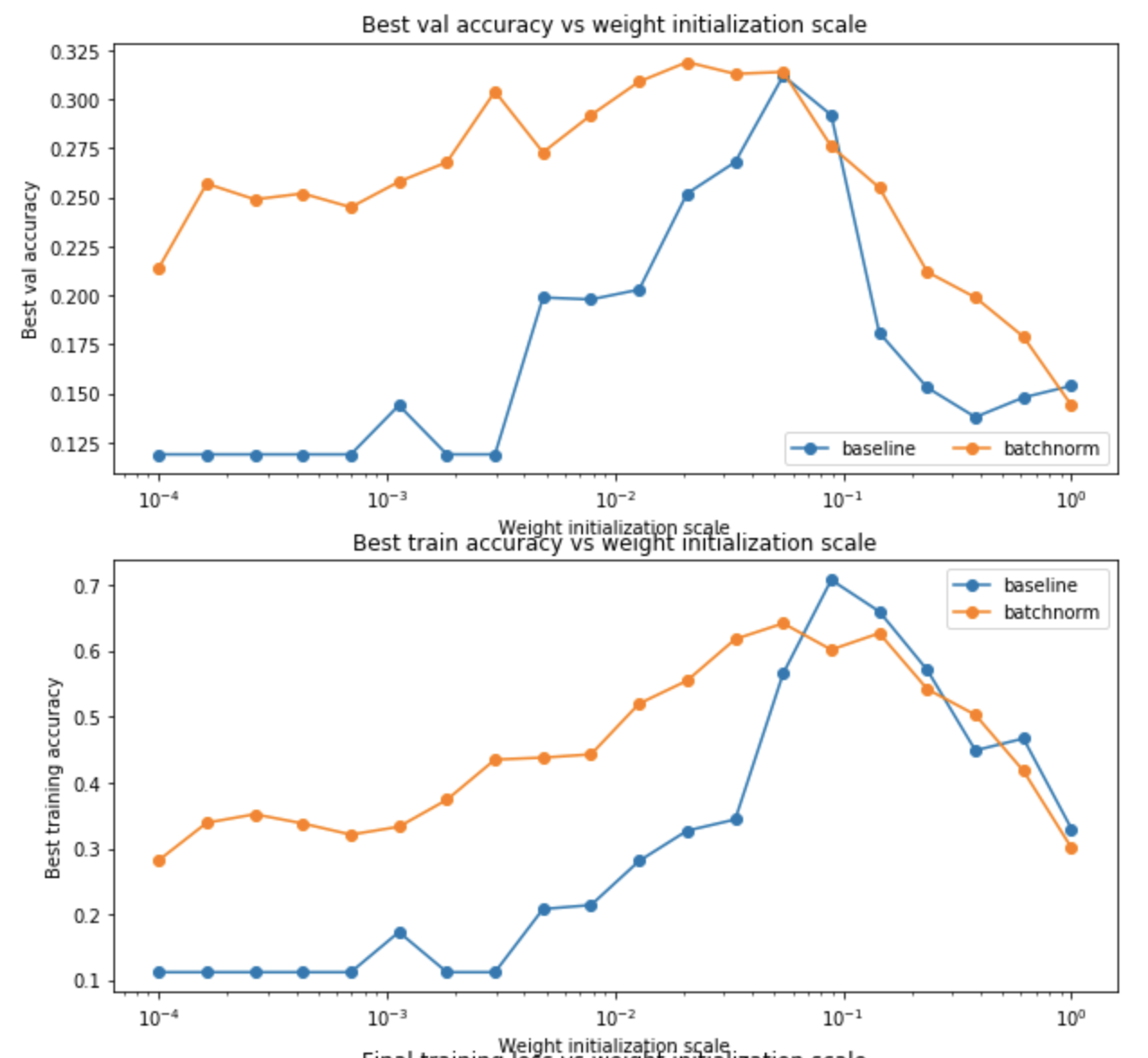
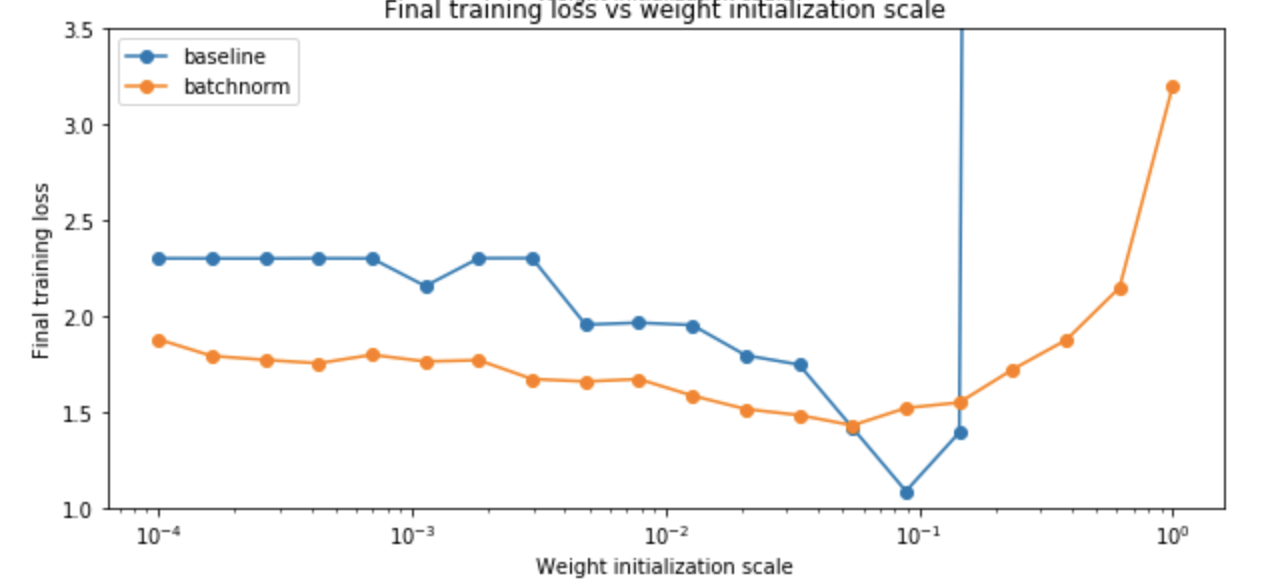
(2)实验2比较了使用和不使用BN的网络,初始化参数w对其性能的影响。发现使用BN的网络对初始化参数有更好的鲁棒性:
3 Dropout
(1)注意区别np.random.randn和np.random.rand,前者是生成服从标准正态分布的随机数,后者是生成0~1之间均匀分布的随机数。
(2)关键代码
Dropout层的前向传播:
if mode == 'train':
mask = (np.random.rand(*x.shape) > p) / p
out = x * mask elif mode == 'test':
out = x
注意这里实现的是inverted dropout,训练阶段通过dropout层乘以因子1/p,则测试阶段乘以p*1/p,刚好抵消,进而提高测试阶段的效率。
Dropout层的反向传播:
if mode == 'train':
dx = dout * mask
elif mode == 'test':
dx = dout
(3)实验
实现了Dropout层的前向传播和反向传播,并加入到全连接网络中查看了正则化效果:

4 卷积神经网络
(1)一些numpy使用方法
①使用np.pad来做零填充。
②np.sum中,axis参数可以是元组,表示经过sum运算后,哪些维度将会消失掉。keepdims参数表示这些维度置为1,不消失。
③np.max中,与np.sum相同,axis参数表示哪些维度会消失掉。keepdims表示保持维度不消失,置为1。这些规则同样适用于np.mean,np.var等。
④特别要注意在进行整数语法切片后维度会丢失,导致广播出错。例如对一个(2,3)维的数组切片[1,:],生成的数组维度不是(1,3)而是(3,)
(2)灰度缩放和边缘检测
为了更好地理解卷积核,我们将滤波器分别设置为灰度缩放和边缘检测的形式:
# The first filter converts the image to grayscale.
# Set up the red, green, and blue channels of the filter.
w[0, 0, :, :] = [[0, 0, 0], [0, 0.0, 0], [0, 0, 0]]
w[0, 1, :, :] = [[0, 0, 0], [0, 0.0, 0], [0, 0, 0]]
w[0, 2, :, :] = [[0, 0, 0], [0, 1, 0], [0, 0, 0]] # Second filter detects horizontal edges in the blue channel.
w[1, 2, :, :] = [[1, 2, 1], [0, 0, 0], [-1, -2, -1]]
这里的边缘检测卷积核又被称为Sobels算子,是计算机视觉中的一种边缘检测方法,详细介绍见https://en.wikipedia.org/wiki/Sobel_operator。我们通俗的理解一下Sobels算子为什么有边缘检测的效果:它的权重和为0,那么当滤波器探测到非边缘的时候(输入值在小窗口上变化不剧烈),输出约为0,当探测到边缘的时候(输入值在小窗口上变化剧烈),滤波器有大的输出。
最后的效果:

(3)卷积层的前向传播和反向传播(naive版)
前向传播:
def conv_forward_naive(x, w, b, conv_param):
"""
A naive implementation of the forward pass for a convolutional layer. The input consists of N data points, each with C channels, height H and
width W. We convolve each input with F different filters, where each filter
spans all C channels and has height HH and width HH. Input:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- 'stride': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- 'pad': The number of pixels that will be used to zero-pad the input. Returns a tuple of:
- out: Output data, of shape (N, F, H', W') where H' and W' are given by
H' = 1 + (H + 2 * pad - HH) / stride
W' = 1 + (W + 2 * pad - WW) / stride
- cache: (x, w, b, conv_param)
"""
out = None
stride = conv_param['stride']
pad = conv_param['pad']
N, C, H, W = x.shape
F, C, HH, WW = w.shape
###########################################################################
# TODO: Implement the convolutional forward pass. #
# Hint: you can use the function np.pad for padding. #
###########################################################################
pad_x = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant')
H_out = int(1 + (H + 2 * pad - HH) / stride)
W_out = int(1 + (W + 2 * pad - WW) / stride)
out = np.zeros((N, F, H_out, W_out))
for i in range(0, H_out):
for j in range(0, W_out):
x_part = pad_x[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
for k in range(0, F):
out[:, k, i, j] = np.sum(x_part * w[k, :, :, :], axis=(1, 2, 3)) + b[k]
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, w, b, conv_param)
return out, cache
反向传播:
def conv_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a convolutional layer. Inputs:
- dout: Upstream derivatives.
- cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive Returns a tuple of:
- dx: Gradient with respect to x
- dw: Gradient with respect to w
- db: Gradient with respect to b
"""
dx, dw, db = None, None, None
x, w, b, conv_param = cache
stride = conv_param['stride']
pad = conv_param['pad']
H, W = (x.shape[2], x.shape[3])
F, C, HH, WW = w.shape
N, F, H_out, W_out = dout.shape
###########################################################################
# TODO: Implement the convolutional backward pass. #
###########################################################################
#cal db
db = np.sum(dout, axis=(0, 2, 3)) #cal dw
dw = np.zeros(w.shape)
pad_x = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant')
for i in range(0, H_out):
for j in range(0, W_out):
x_part = pad_x[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
for k in range(0, F):
dw[k, :, :, :] += np.sum(x_part * dout[:, k, i, j].reshape(N, 1, 1, 1), axis=0) #cal dpad_x, dx
dpad_x = np.zeros(pad_x.shape)
for i in range(0, H_out):
for j in range(0, W_out):
dpad_x_part = dpad_x[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
for k in range(0, F):
dpad_x_part += dout[:, k, i, j].reshape(N, 1, 1, 1) * w[k, :, :, :]
dx = dpad_x[:, :, pad:pad+H, pad:pad+W]
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
卷积层的反向传播实现是一个难点,具体细节要好好琢磨代码,涉及到了大量的数组广播。实现的大体思路是:先考虑激活图中单个神经元的梯度是如何往回传的,然后遍历激活图,注意当不同路径的梯度传到同一个节点时,需要相加。
(4)max pooling层的前向传播和反向传播(naive版)
相比于卷积层,max pooling层很简单了。
前向传播:
def max_pool_forward_naive(x, pool_param):
"""
A naive implementation of the forward pass for a max pooling layer. Inputs:
- x: Input data, of shape (N, C, H, W)
- pool_param: dictionary with the following keys:
- 'pool_height': The height of each pooling region
- 'pool_width': The width of each pooling region
- 'stride': The distance between adjacent pooling regions Returns a tuple of:
- out: Output data
- cache: (x, pool_param)
"""
out = None
N, C, H, W = x.shape
HH = pool_param['pool_height']
WW = pool_param['pool_width']
stride = pool_param['stride']
###########################################################################
# TODO: Implement the max pooling forward pass #
###########################################################################
H_out = int(1 + (H - HH) / stride)
W_out = int(1 + (W - WW) / stride)
out = np.zeros((N, C, H_out, W_out))
for i in range(0, H_out):
for j in range(0, W_out):
x_part = x[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
out[:, :, i, j] = np.max(x_part, axis=(2, 3))
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, pool_param)
return out, cache
反向传播:
def max_pool_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a max pooling layer. Inputs:
- dout: Upstream derivatives
- cache: A tuple of (x, pool_param) as in the forward pass. Returns:
- dx: Gradient with respect to x
"""
dx = None
x, pool_param = cache
N, C, H, W = x.shape
HH = pool_param['pool_height']
WW = pool_param['pool_width']
stride = pool_param['stride']
_, _, H_out, W_out = dout.shape
###########################################################################
# TODO: Implement the max pooling backward pass #
###########################################################################
dx = np.zeros(x.shape)
for i in range(0, H_out):
for j in range(0, W_out):
dx_part = dx[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
x_part = x[:, :, i * stride:i * stride + HH, j * stride:j * stride + WW]
dx_part += (np.max(x_part, axis=(2,3), keepdims=True) == x_part) * dout[:, :, i:i+1, j:j+1]
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
(5) fast layer
作业中还给我们提供了卷积层和max pooling层的高效实现(不需要我们自己实现),这个实现基于Cython。
(6) 卷积网络中的Batch Normalization
卷积网络中,我们需要将处于同一个深度切面上的所有激活使用同样的方式标准化,因此需要在N*H*M上求均值和方差(标准的BN是在N上求均值方差),并且gamma和beta的大小为激活的深度C,即同一个深度切面使用同一个gamma和beta。对标准的Batch Normalization略做修改即可得到卷积网络中的Batch Normalization,称为空间Batch Normalization。实现如下:
前向传播:
def spatial_batchnorm_forward(x, gamma, beta, bn_param):
"""
Computes the forward pass for spatial batch normalization. Inputs:
- x: Input data of shape (N, C, H, W)
- gamma: Scale parameter, of shape (C,)
- beta: Shift parameter, of shape (C,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance. momentum=0 means that
old information is discarded completely at every time step, while
momentum=1 means that new information is never incorporated. The
default of momentum=0.9 should work well in most situations.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features Returns a tuple of:
- out: Output data, of shape (N, C, H, W)
- cache: Values needed for the backward pass
""" out, cache = None, None
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
C = x.shape[1]
running_mean = bn_param.get('running_mean', np.zeros((1, C, 1, 1), dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros((1, C, 1, 1), dtype=x.dtype))
###########################################################################
# TODO: Implement the forward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization using the vanilla #
# version of batch normalization defined above. Your implementation should#
# be very short; ours is less than five lines. #
###########################################################################
if bn_param['mode'] == 'train':
sample_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
sample_var = np.var(x, axis=(0, 2, 3), keepdims=True)
normal_x = (x - sample_mean) / np.sqrt(sample_var + eps)
out = gamma.reshape(1, C, 1, 1) * normal_x + beta.reshape(1, C, 1, 1)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
cache = (gamma, beta, sample_mean, sample_var, normal_x, eps, x)
else:
normal_x = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma.reshape(1, C, 1, 1) * normal_x + beta.reshape(1, C, 1, 1)
###########################################################################
# END OF YOUR CODE #
###########################################################################
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var return out, cache
反向传播:
def spatial_batchnorm_backward(dout, cache):
"""
Computes the backward pass for spatial batch normalization. Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
dx, dgamma, dbeta = None, None, None
gamma, beta, sample_mean, sample_var, normal_x, eps, x = cache
N, C, H, W = x.shape
m = N * H * W
C = dout.shape[1]
###########################################################################
# TODO: Implement the backward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization using the vanilla #
# version of batch normalization defined above. Your implementation should#
# be very short; ours is less than five lines. #
###########################################################################
dnormal_x = dout * gamma.reshape(1, C, 1, 1)
dvar = np.sum(dnormal_x * (x - sample_mean), axis=(0, 2, 3), keepdims=True) * (-0.5) * (sample_var + eps) ** (-1.5)
dmean = np.sum(-1 / np.sqrt(sample_var + eps) * dnormal_x, axis=(0, 2, 3), keepdims=True) + dvar * np.sum(-2 * (x - sample_mean), axis=(0, 2, 3), keepdims=True) / m
dx = 1 / np.sqrt(sample_var + eps) * dnormal_x + dvar * 2 * (x - sample_mean) / m + dmean / m
dgamma = np.sum(dout * normal_x, axis=(0, 2, 3))
dbeta = np.sum(dout, axis=(0, 2, 3))
###########################################################################
# END OF YOUR CODE #
########################################################################### return dx, dgamma, dbeta
Spring 2017 Assignments2的更多相关文章
- cs231n spring 2017 lecture13 Generative Models 听课笔记
1. 非监督学习 监督学习有数据有标签,目的是学习数据和标签之间的映射关系.而无监督学习只有数据,没有标签,目的是学习数据额隐藏结构. 2. 生成模型(Generative Models) 已知训练数 ...
- cs231n spring 2017 lecture11 Detection and Segmentation 听课笔记
1. Semantic Segmentation 把每个像素分类到某个语义. 为了减少运算量,会先降采样再升采样.降采样一般用池化层,升采样有各种"Unpooling"." ...
- cs231n spring 2017 lecture9 CNN Architectures 听课笔记
参考<deeplearning.ai 卷积神经网络 Week 2 听课笔记>. 1. AlexNet(Krizhevsky et al. 2012),8层网络. 学会计算每一层的输出的sh ...
- cs231n spring 2017 lecture7 Training Neural Networks II 听课笔记
1. 优化: 1.1 随机梯度下降法(Stochasitc Gradient Decent, SGD)的问题: 1)对于condition number(Hessian矩阵最大和最小的奇异值的比值)很 ...
- cs231n spring 2017 lecture13 Generative Models
1. 非监督学习 监督学习有数据有标签,目的是学习数据和标签之间的映射关系.而无监督学习只有数据,没有标签,目的是学习数据额隐藏结构. 2. 生成模型(Generative Models) 已知训练数 ...
- cs231n spring 2017 lecture11 Detection and Segmentation
1. Semantic Segmentation 把每个像素分类到某个语义. 为了减少运算量,会先降采样再升采样.降采样一般用池化层,升采样有各种“Unpooling”.“Transpose Conv ...
- cs231n spring 2017 lecture9 CNN Architectures
参考<deeplearning.ai 卷积神经网络 Week 2 听课笔记>. 1. AlexNet(Krizhevsky et al. 2012),8层网络. 学会计算每一层的输出的sh ...
- cs231n spring 2017 lecture7 Training Neural Networks II
1. 优化: 1.1 随机梯度下降法(Stochasitc Gradient Decent, SGD)的问题: 1)对于condition number(Hessian矩阵最大和最小的奇异值的比值)很 ...
- cs231n spring 2017 lecture16 Adversarial Examples and Adversarial Training 听课笔记
(没太听明白,以后再听) 1. 如何欺骗神经网络? 这部分研究最开始是想探究神经网络到底是如何工作的.结果人们意外的发现,可以只改变原图一点点,人眼根本看不出变化,但是神经网络会给出完全不同的答案.比 ...
随机推荐
- [转载] 管Q某犇借的手写堆
跟gxy大神还有yzh大神学了学手写的堆,应该比stl的优先队列快很多. 其实就是维护了一个二叉堆,写进结构体里,就没啥了... 据说达哥去年NOIP靠这个暴力多骗了分 合并果子... templat ...
- 数据结构-树以及深度、广度优先遍历(递归和非递归,python实现)
前面我们介绍了队列.堆栈.链表,你亲自动手实践了吗?今天我们来到了树的部分,树在数据结构中是非常重要的一部分,树的应用有很多很多,树的种类也有很多很多,今天我们就先来创建一个普通的树.其他各种各样的树 ...
- Spring MVC源码(四) ----- 统一异常处理原理解析
SpringMVC除了对请求URL的路由处理特别方便外,还支持对异常的统一处理机制,可以对业务操作时抛出的异常,unchecked异常以及状态码的异常进行统一处理.SpringMVC既提供简单的配置类 ...
- TreeMap原理实现及常用方法
目录 一. TreeMap概述 二. 红黑树回顾 三. TreeMap构造 四. put方法 五. get 方法 六. remove方法 七. 遍历 八. 总结 前面我们分别讲了Map接口的两个实现类 ...
- 洛谷P3324 [SDOI2015]星际战争 题解
题目链接: https://www.luogu.org/problemnew/show/P3324 分析: 因为本题的时间点较多,不能枚举,但发现有单调性,于是二分答案,二分使用的时间TTT 每个攻击 ...
- 个人永久性免费-Excel催化剂功能第85波-灵活便捷的批量发送短信功能(使用腾讯云接口)
微信时代的今天,短信一样不可缺席,大系统都有集成短信接口.若只是临时用一下,若能够直接在Excel上加工好内容就可以直接发送,这些假设在此篇批量群发短信功能中都为大家带来完美答案. 业务场景 不多说, ...
- C#4.0新增功能03 泛型中的协变和逆变
连载目录 [已更新最新开发文章,点击查看详细] 协变和逆变都是术语,前者指能够使用比原始指定的派生类型的派生程度更大(更具体的)的类型,后者指能够使用比原始指定的派生类型的派生程度更小(不太具体 ...
- 小白开学Asp.Net Core 《九》
小白开学Asp.Net Core <九> — — 前端篇(不务正业) 在<小白开学Asp.Net Core 三>中使用了X-admin 2.x 和 Layui将管理后端的界面重 ...
- Go语言圣经习题练习_1.6并发获取多个URL
练习 1.10: 找一个数据量比较大的网站,用本小节中的程序调研网站的缓存策略,对每个URL执行两遍请求,查看两次时间是否有较大的差别,并且每次获取到的响应内容是否一致,修改本节中的程序,将响应结果输 ...
- ASP.NET Core Web Api之JWT VS Session VS Cookie(二)
前言 本文我们来探讨下JWT VS Session的问题,这个问题本没有过多的去思考,看到评论讨论太激烈,就花了一点时间去研究和总结,顺便说一句,这就是写博客的好处,一篇博客写出有的可能是经验积累,有 ...
