ccf-csp201809题解

标签（空格分隔）： ccf题解

ccf-csp201809题解

1. 201809-1 卖菜

题目描述

试题编号： 201809-1

试题名称：卖菜

时间限制： 1.0s

内存限制： 256.0MB

问题描述

　　在一条街上有n个卖菜的商店，按1至n的顺序排成一排，这些商店都卖一种蔬菜。

　　第一天，每个商店都自己定了一个价格。店主们希望自己的菜价和其他商店的一致，第二天，每一家商店都会根据他自己和相邻商店的价格调整自己的价格。具体的，每家商店都会将第二天的菜价设置为自己和相邻商店第一天菜价的平均值（用去尾法取整）。

　　注意，编号为1的商店只有一个相邻的商店2，编号为n的商店只有一个相邻的商店n-1，其他编号为i的商店有两个相邻的商店i-1和i+1。

　　给定第一天各个商店的菜价，请计算第二天每个商店的菜价。

输入格式

　　输入的第一行包含一个整数n，表示商店的数量。

　　第二行包含n个整数，依次表示每个商店第一天的菜价。

输出格式

　　输出一行，包含n个正整数，依次表示每个商店第二天的菜价。

样例输入

8

4 1 3 1 6 5 17 9

样例输出

2 2 1 3 4 9 10 13

数据规模和约定

　　对于所有评测用例，2 ≤ n ≤ 1000，第一天每个商店的菜价为不超过10000的正整数。

解析

依题意，先将输入的数据用数组存下来（也可以使用在线做法），然后用$O(n)$的复杂度跑一遍，依次输出相邻三个数的平均值。

通过代码

//1591298	<13100928923>	<王恪楠>	卖菜	11-09 21:28	409B	C0X	正确	100	15ms	532.0KB
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e3 + 50;
int a[MAXN];
int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++)
        scanf("%d", &a[i]);
    for(int i = 1; i <= n; i ++){
        int t = (a[i - 1] + a[i] + a[i + 1]);
        if(i == 1 || i == n)                  //第一个数和最后一个数的相邻数只有一个，所以求平均数只除以2.
            printf("%d ", t / 2);
        else
            printf("%d ", t / 3);
    }
    return 0;
}

2. 201809-2 买菜

题目描述

试题编号： 201809-2

试题名称：买菜

时间限制： 1.0s

内存限制： 256.0MB

问题描述

　　小H和小W来到了一条街上，两人分开买菜，他们买菜的过程可以描述为，去店里买一些菜然后去旁边的一个广场把菜装上车，两人都要买n种菜，所以也都要装n次车。具体的，对于小H来说有n个不相交的时间段[a1,b1],[a2,b2]...[an,bn]在装车，对于小W来说有n个不相交的时间段[c1,d1],[c2,d2]...[cn,dn]在装车。其中，一个时间段[s, t]表示的是从时刻s到时刻t这段时间，时长为t-s。

　　由于他们是好朋友，他们都在广场上装车的时候会聊天，他们想知道他们可以聊多长时间。

输入格式

　　输入的第一行包含一个正整数n，表示时间段的数量。

　　接下来n行每行两个数ai，bi，描述小H的各个装车的时间段。

　　接下来n行每行两个数ci，di，描述小W的各个装车的时间段。

输出格式

　　输出一行，一个正整数，表示两人可以聊多长时间。

样例输入

4

1 3

5 6

9 13

14 15

2 4

5 7

10 11

13 14

样例输出

3

数据规模和约定

　　对于所有的评测用例，1 ≤ n ≤ 2000, ai < bi < ai+1，ci < di < ci+1,对于所有的i(1 ≤ i ≤ n)有，1 ≤ ai, bi, ci, di ≤ 1000000。

解析

因为两个人自己装车的区间不会重合，那么我们就将两个人的装车区间打上标记，然后所有被打过两次标记的区间就都是所求。可以用$vis[1\cdots m]$数组记录区间打标记情况。

因为输入所给的$a_i,b_i(c_i, d_i)$分别是区间的左右端点，而不是区间的编号，所以我们在进行标记的时候要注意标记区间而不是区间端点。具体做法就是对于$[l, r)$内的点进行标记（$l$区间左端点，$r$区间右端点）。

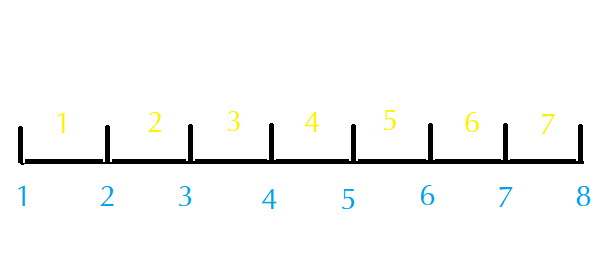
蓝色数字为区间端点序号，黄色数字为区间编号

通过代码

//1591321	<13100928923>	<王恪楠>	买菜	11-09 21:42	473B	C0X	正确	100	15ms	4.335MB
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 50;
int vis[MAXN];
int main()
{
    int n, m = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n + n; i ++){
        int l, r;
        scanf("%d%d", &l, &r);
        m = max(m, r);
        for(int j = l; j < r; j ++)       //将每个区间长度[l,r)打上标记.
            vis[j] ++;
    }
    int ans = 0;
    for(int i = 1; i <= m; i ++)
        if(vis[i] == 2)         //如果一个单位长度被打过两次标记，说明这个单位长度是两人共同装车的时间.
            ans ++;
    printf("%d", ans);
    return 0;
}

3.201809-3 元素选择器

题目描述

试题编号： 201809-3

试题名称：元素选择器

时间限制： 1.0s

内存限制： 256.0MB

解析

大致题意：

我们想要对一个树形（or森林）的字符串结构体进行查找操作。

输入：

第一行为n和m。分别代表输入的字符串个数，和查询个数。

下面的n行每行为一个字符串。给出n个结构体。每行的字符串都以"."为起始且点的个数只能为偶数个（可以为0个），代表这一结构体的缩进等级。（缩进等级大的结构体的前缀为与其最近的等级减2的结构体。）之后的字符串为该结构体的标签（不区分大小写，可统一化为小写），之后如果有"#"，则"#"之后的字符串为该结构体的id，id区分大小写，且唯一。

下面的m行每行为一个字符串。给出m个查询操作。

1.形如"tag"的字符串，查询标签为"tag"的结构体的序号。

2.形如"#id"的字符串，查询id为"id"的结构体的序号。

3.形如"tag tag #id #id ..."的字符串，查询从左至右，是否每前一个结构体为后一个结构体的前缀，如果满足，则记录最后一个结构体的序号。遇到"tag"则是对比结构体标签，遇到"#id"对比结构体id。

输出：

将每一个查询得到的序号从小到大输出，然后输出换行。

我们可以用一个结构体来储存每一行的缩进等级(int)，标签（string），id（string）。

对于查询1和查询2较为简单，因为数据规模较小，我们可以简单的$O(n)$实现。

对于查询3，我们需要用一个栈将所要查询的字符串先储存下来，然后找到栈顶的结构体，再用它的前缀不断递归一一和栈中元素对比。

通过代码

//1599261	<13100928923>	<王恪楠>	元素选择器	11-14 21:00	3.233KB	C0X	正确	100	15ms	632.0KB
#include <bits/stdc++.h>
using namespace std;
struct Node
{
    int fa;
    string tag, id;       //fa是结构体的父亲节点的序号，tag是标签，id是id值.
}a[500];
int last[500], top;      //last是存储每一个缩进等级的最近节点序号，比它小一级(值-2)的节点都以此节点为父亲节点.
string s0, s[500];       //用s[1...n]和top模拟栈.后代选择器时使用.
vector<int> ans;         //用以记录答案的向量.
ostream &operator << (ostream &out, const Node &i)     //重载<<，输出结构体.（测试程序时用）
{
    cout << i.tag << " " << i.id << " " << i.fa;
    return out;
}
bool cmp(int i, string ss)     //比较函数.如果字符串带#则和id比较.如果字符串不带#则和tag比较，和tag比较时00不区分大小写.
{
    string str;
    if(ss[0] == '#'){
        for(int j = 1; j < ss.length(); j ++)
            str += ss[j];
        return a[i].id == str;
    }
    transform(ss.begin(), ss.end(), ss.begin(), ::tolower);     //将ss都转变为小写，再和tag作比较.
    return a[i].tag == ss;
}
int getfa(int i)          //后代选择器.不断地寻找节点的父亲节点，和栈顶字符串作比较.如果能使栈为空，说明后代选择器的所有祖先字符串都能被找到.
{
    if(i == 0){          //当找到第一缩进等级，节点没有父亲节点时，就要返回！top的值了.
        return !top;
    }
    if(top == 0){
        return 1;
    }
    if(cmp(i, s[top - 1])){
        top --;
    }
    return getfa(a[i].fa);
}
void print()
{
    printf("%d", ans.size());
    for(int i = 0; i < ans.size(); i ++)
        printf(" %d", ans[i]);
    printf("\n");
    return ;
}
void split(string ss)           //字符串分割，以空格为分割符.分割后入栈.
{
    string str;
    for(int i = 0; i < ss.length(); i ++){
        if(ss[i] == ' '){
            s[top ++] = str;
            str.clear();
        }
        else
            str += ss[i];
    }
    s[top ++] = str;
    return;
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);getchar();
    for(int i = 1; i <= n; i ++){
        getline(cin, s0);                         //getline()可以整行输入字符串，而不是遇到空格就停止.
        int level, pos = 0, flag = 1;
        for(int j = 0; j < s0.length(); j ++){
            if(s0[j] != '.' && flag){            //记录缩进等级.
                level = j;
                flag = 0;
            }
            if(s0[j] == '#')                     //判断是否有id.
                pos = j;
        }
        last[level] = i;                        //这个缩进等级的最近一个序号更新为这个节点的序号.
        if(level == 0)
            a[i].fa = 0;                       //如果是第零级，那么它就没有祖先节点，就为0.
        else
            a[i].fa = last[level - 2];        //否则最近的上一缩进等级的序号就是该节点的祖先.
        string tag;
        for(int j = level; j < s0.length() && s0[j] != ' '; j ++)
            tag += s0[j];
        transform(tag.begin(), tag.end(), tag.begin(), ::tolower);
        a[i].tag = tag;                                  //存下标签tag（注意tag不区分大小写，那么就统一用小写字母存）.
        if(pos){
            string id;
            for(int j = pos + 1; j < s0.length(); j ++)  //存下id.
                id += s0[j];
            a[i].id = id;
        }
    }
    while(m --){
        getline(cin, s0);
        ans.clear();
        top = 0;
        split(s0);                //分割字符串.如果只有一个字符串，也没有影响.
        string t = s[top - 1];
        top --;
        int mm = top;
        for(int i = 1; i <= n; i ++)
        if(cmp(i, t)){                 //将各个节点和栈顶字符串作比较.
            top = mm;                  //每次查找祖先时，将栈顶指针还原，即将栈还原.
            if(getfa(a[i].fa))
                ans.push_back(i);
        }
        print();
    }
    return 0;
}

4.201809-4 再卖菜

题目描述

试题编号： 201809-4

试题名称：再卖菜

时间限制： 1.0s

内存限制： 256.0MB

问题描述

　　在一条街上有n个卖菜的商店，按1至n的顺序排成一排，这些商店都卖一种蔬菜。

　　第一天，每个商店都自己定了一个正整数的价格。店主们希望自己的菜价和其他商店的一致，第二天，每一家商店都会根据他自己和相邻商店的价格调整自己的价格。具体的，每家商店都会将第二天的菜价设置为自己和相邻商店第一天菜价的平均值（用去尾法取整）。

　　注意，编号为1的商店只有一个相邻的商店2，编号为n的商店只有一个相邻的商店n-1，其他编号为i的商店有两个相邻的商店i-1和i+1。

　　给定第二天各个商店的菜价，可能存在不同的符合要求的第一天的菜价，请找到符合要求的第一天菜价中字典序最小的一种。

　　字典序大小的定义：对于两个不同的价格序列(a1, a2, ..., an)和(b1, b2, b3, ..., bn)，若存在i (i>=1), 使得ai<bi，且对于所有j<i，aj=bj，则认为第一个序列的字典序小于第二个序列。

输入格式

　　输入的第一行包含一个整数n，表示商店的数量。

　　第二行包含n个正整数，依次表示每个商店第二天的菜价。

输出格式

　　输出一行，包含n个正整数，依次表示每个商店第一天的菜价。

样例输入

8

2 2 1 3 4 9 10 13

样例输出

2 2 2 1 6 5 16 10

数据规模和约定

　　对于30%的评测用例，2<=n<=5，第二天每个商店的菜价为不超过10的正整数；

　　对于60%的评测用例，2<=n<=20，第二天每个商店的菜价为不超过100的正整数；

　　对于所有评测用例，2<=n<=300，第二天每个商店的菜价为不超过100的正整数。

　　请注意，以上都是给的第二天菜价的范围，第一天菜价可能会超过此范围。

解析

本题所考察的知识点是差分约束系统。在白书最短路算法的最后一道例题讲对差分约束系统有所讲解。

CSDN 差分约束算法总结 by Dust_Heart

本题如何建图？

设第$i$个菜店第一天的菜价为$b[i]\,$,第二天的菜价（即第一天相邻店铺菜价的平均值）为$a[i]$，$\sum_{i=0}^{n}b[i] = d[n]$（即$b[i]$的前缀和为$d[i]$）。

因为差分约束系统不等式一侧只能有两个变量，所以$d[i]$为前缀和，即可一般地，把$a[i]$相邻的三个数$b[i-1],b[i],b[i+1]$的平均值不等式表达为$3 * a[i] \leq d[i + 1] - d[i - 2] \leq 3*a[i] + 2$.
本题是希望找到最小的$b[i]$，即是想找到最小的$d[i] - d[i - 1]$，对应于差分约束系统需要建立形如$v - u \geq w$的不等式组，同时建立一条起点为$u$，终点为$v$，权值为$w$的边，然后找出不等式组的最大值。
当$i\in[2, n - 1]$时，$$3 * a[i] \leq d[i + 1] - d[i - 2] \leq 3*a[i] + 2 \Rightarrow

\begin{cases}

d[i+1] - d[i - 2] \geq 3 * a[i], \

d[i - 2] - d[i + 1] \geq -3 * a[i] - 2.

\end{cases}$$
因为首尾只有两个店铺和它们相邻，所以当$i \in \{1, n\}\,$时，$$

\begin{cases}

d[2] - d[0] \geq 2 * a[1], \

d[0] - d[2] \geq -2 * a[1] - 1;

\end{cases};;

\begin{cases}

d[n] - d[n - 2] \geq 2 * a[n], \

d[n - 2] - d[n] \geq -2 * a[n] - 1.

\end{cases}$$
将形如不等式$v - u \geq w$添加一条$u \to v$的权值为$w$的边。

当我们通过上述方法完成建图之后，就只要虚拟一个起始源点用dijsktra跑一遍找出单源最长路即可。

通过代码

//1613829	<13100928923>	<王恪楠>	再卖菜	11-21 21:22	1.678KB	C0X	正确	100	15ms	576.0KB
#include <bits/stdc++.h>
#define to first
#define coast second
using namespace std;
const int MAXN = 5e2;
typedef pair<int, int> P;
int a[MAXN], s[MAXN], d[MAXN], n;
vector<P> G[MAXN];
void add_edge(int u, int v, int w)
{
    G[u].push_back(P(v, w));
    return;
}
void dijsktra()                    //用dijsktra算法求最长路，把最短路的写法反过来写.
{
    priority_queue<P> q;
    d[0] = 0;
    q.push(P(0, 0));
    while(!q.empty()){
        P p = q.top();
        q.pop();
        int v = p.second;
        if(d[v] > p.first)   continue;
        for(int i = 0; i < G[v].size(); i ++){
            P e = G[v][i];
            if(d[e.to] < d[v] + e.coast){
                d[e.to] = d[v] + e.coast;
                q.push(P(d[e.to], e.to));
            }
        }
    }
    return;
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++)
        scanf("%d", &a[i]);
    //加边建图.
    for(int i = 2; i < n; i ++){
        add_edge(i - 2, i + 1, 3 * a[i]);
        add_edge(i + 1, i - 2, -3 * a[i] - 2);
    }
    add_edge(0, 2, 2 * a[1]);
    add_edge(2, 0, -2 * a[1] - 1);
    add_edge(n - 2, n, 2 * a[n]);
    add_edge(n, n - 2, -2 * a[n] - 1);
    for(int i = 1; i <= n; i ++)
        add_edge(i - 1, i, 1);
    dijsktra();     //跑一遍dijsktra.
    for(int i = 1; i <= n; i ++)
        printf("%d ", d[i] - d[i - 1]);          //d[i]是前缀和数组.
    return 0;
}