OO第三单元作业总结

OO第三单元作业总结——JML

第三单元的主题是JML规格的学习，其中的三次作业也是围绕JML规格的实现所展开的（虽然感觉作业中最难的还是如何正确适用数据结构以及如何正确地对于时间复杂度进行优化）。

---

关于JML语言

• JML语言概述

  JML是Java Modeling Language的缩写，意思是Java建模语言，是一种进行详细设计的符号语言。

  使用JML语言的好处主要有以下几点：

  1. 能够描述类和方法的运行方式，从而使代码的编写过程更加契合面向对象思想；
  2. 可以更加高效地发现和修正程序中的bug
  3. 在程序开发中降低bug的出现几率并及时发现已有的bug

  所以说，JML对于面向对象的学习还是有很大的帮助的。

• JML基本语法

  下面总结一下目前JML学习中使用到的常用语法：

  • JML表达式

    原子表达式：

    \result表达式：表示方法执行后的返回值。

    \old( expr )表达式：用来表示一个表达式 expr 在相应方法执行前的取值。

    量化表达式：

    \forall表达式：全称量词修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。例如(\forall int i,j; 0 <= i && i < j && j < 10; a[i] < a[j])

    \exists表达式：存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。例如(\exists int i; 0 <= i && i < 10; a[i] < 0)

    \sum表达式：返回给定范围内的表达式的和。例如， (\sum int i; 0 <= i && i < 5; i)

    此外，还有集合表达式、包含操作符的表达式等。

  • 方法规格

    1. 前置条件：通过requires子句来表示；

    2. 后置条件：通过ensures子句来表示；

    3. 副作用范围限定：通过使用关键词 assignable 或者modifiable限定，其中 assignable 表示可赋值，而 modifiable 则表示可修改；

       异常区分：使用signals子句，signals子句的结构为 signals (Exception e) b_expr，表示当 b_expr 为 true 时，方法会抛出括号中给出的相应异常e。

  • 类型规格

    • 不变式invariant：不变式是要求在所有可见状态下都必须满足的特性，语法上定义 invariant P；
    • 状态变化约束constraint：用constraint来对前序可见状态和当前可见状态的关系进行约束。

• JML应用工具链

  • OpenJML：检查JML的语法和逻辑。
  • JMLUnit/JMLUnitNG：根据JML自动生成测试样例。

---

部署SMT Solver

在多次尝试试用各种方式安装openJML后，终于可以基本对于程序使用SMT Solver进行测试。

测试命令（windows环境）：

java -jar path1\openjml.jar -check path2\classname.java

（其中，path1为openjml解压到的文件夹，path2位需进行测试的java程序所在的位置）

最开始，我先对于OpenJML网站上的最简单的程序进行了测试，代码如下：

public class MaybeAdd {
    //@ requires a > 0;
    //@ requires b > 0;
    //@ ensures \result == a+b;
    public static int add(int a, int b){
        return a-b;
    }

    public static void main(String args[]){
        System.out.println(add(2,3));
    }
}

测试并没有报出错误，为了检测这种测试方法的正确性，我改了原代码中requires中的==，将其改为了=，再次进行测试：

public class MaybeAdd {
    //@ requires a > 0;
    //@ requires b > 0;
    //@ ensures \result = a+b;  //此处发生改变
    public static int add(int a, int b){
        return a-b;
    }

    public static void main(String args[]){
        System.out.println(add(2,3));
    }
}

此次，测试报出两个错误，表明等号位置发生错误：

由于使用SMT Solver测试经常出现一些不可知的错误，所以这回我只选用了一个MyPath类中非常简单的方法进行了测试：

public class GetNode {
    private  /*@spec_public@*/ int[] nodes;

    /*@ requires index >= 0 && index < nodes.length;
      @ assignable \nothing;
      @ ensures \result == nodes[index];
      @*/
    public int getNode(int index) {
        return nodes[index];
    }
}

测试没有报错，表示程序正确。

此时改变代码中的nodes.length为nodes.size()：

public class GetNode {
    private  /*@spec_public@*/ int[] nodes;

    /*@ requires index >= 0 && index < nodes.size();
      @ assignable \nothing;
      @ ensures \result == nodes[index];
      @*/
    public int getNode(int index) {
        return nodes[index];
    }
}

测试报出一个错误，如下图所示：

---

部署JMLUnitNG/JMLUnit

由于之前的代码的jml规格中存在不少问题，所以这回我还是使用官网给出的简易demo先进行测试：

public class MaybeAdd {
    //@ requires a > 0;
    //@ requires b > 0;
    //@ ensures \result == a+b;
    public static int add(int a, int b){
        return a-b;
    }

    public static void main(String args[]){
        System.out.println(add(2,3));
    }
}

测试命令与SMT Solver类似：

java -jar path1\jmlunitng.jar path2\classname.java

最终产生的测试文件如下图：

同样，对于MyPath类中getNode方法进行生成测试文件：

public class GetNode {
    private  /*@spec_public@*/ int[] nodes;

    /*@ requires index >= 0 && index < nodes.length;
      @ assignable \nothing;
      @ ensures \result == nodes[index];
      @*/
    public int getNode(int index) {
        return nodes[index];
    }
}

最终生成的测试文件如下：

---

梳理架构设计与BUG分析

这个单元的作业可以说是至今为止最差的几次，虽然在JML的理解上是没有出现什么问题的，但是由于数据结构上使用的错误，以及算法优化的问题，导致在代码的实现方面出现了很大的问题。

第一次作业

• 类图

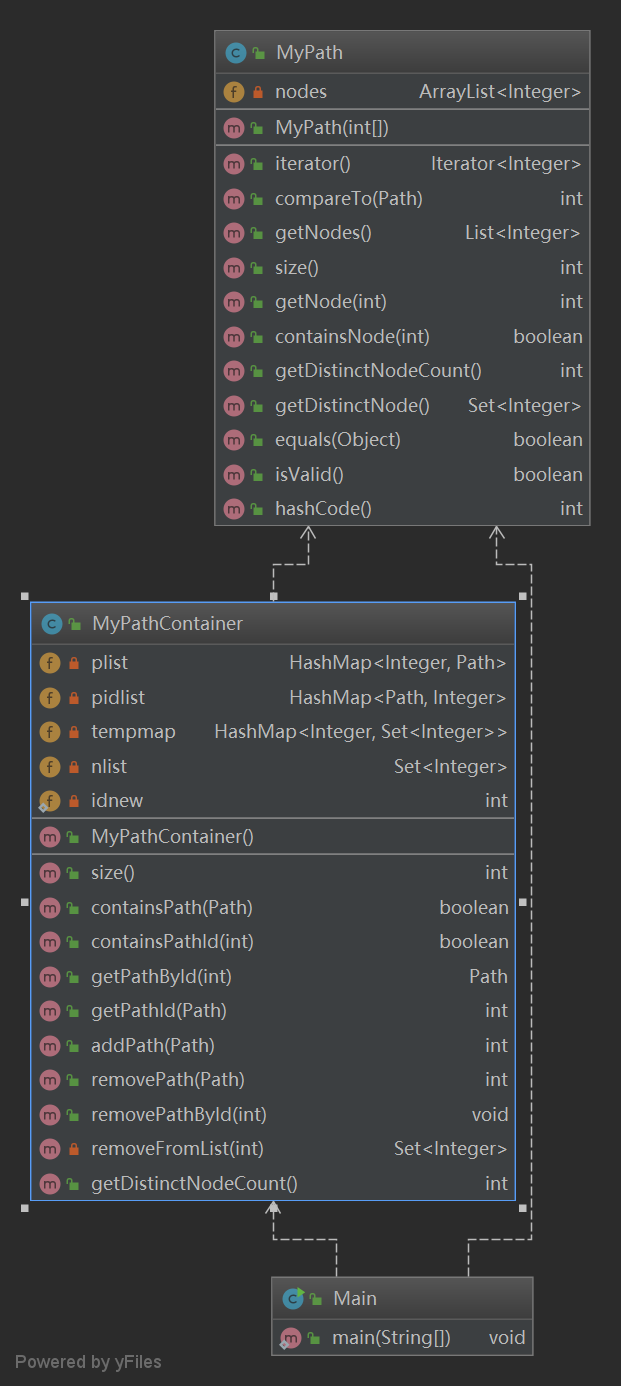
这次的架构基本就是按照指导书的要求写的，分为了Main，Mypath和MyPathContainer三个类。

• 主要度量图

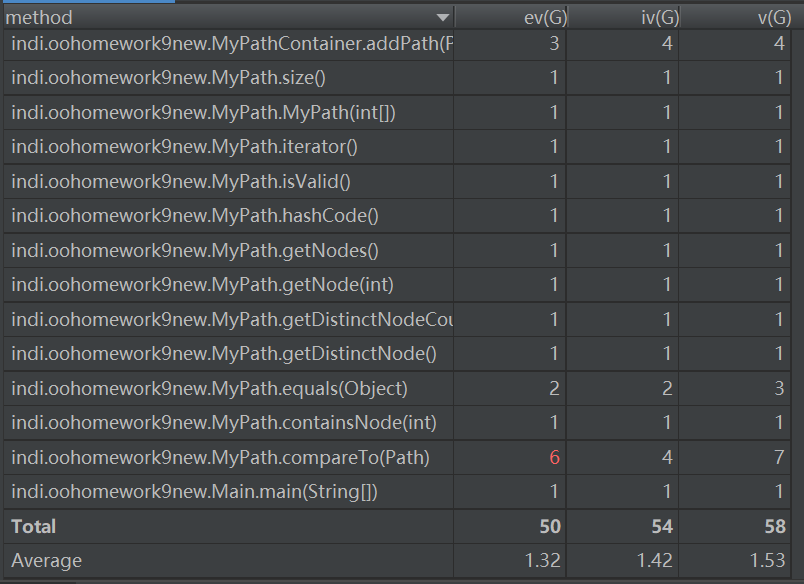
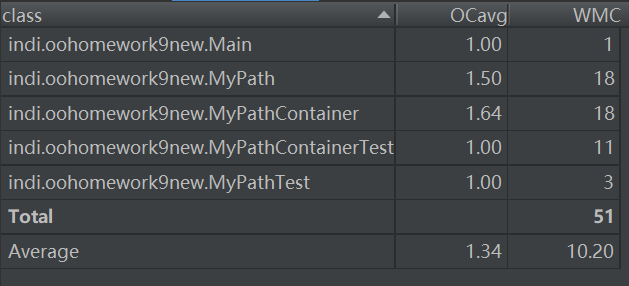
从度量图中可以看出，由于第一次作业较为简单，所以每个类和方法的复杂度都还是比较低的。

• bug分析

  这单元第一次作业其实非常简单，但是需要考虑的方面还是比较多的。一方面是对于数据容器的选择，在这方面我使用的是hashmap，可以在查找时尽量保证复杂度为O(1)。另一方面是如何分配操作的位置，在这一方面我栽了跟头，没能注意到加减道路的指令比查不同点的数目的指令的数量少的多，所以可以将找不同点的数目这一运算分散到加减路径的操作中，而这个问题也使我在强测中TLE了不少点。

  修改方法：

  使用一个hashset进行点的储存，可以直接防止重复加点，并且将加点操作分散到加减路径中，代码修改即为：

  public int getDistinctNodeCount() {
          return nlist.size();
  }
  

第二次作业

• 类图

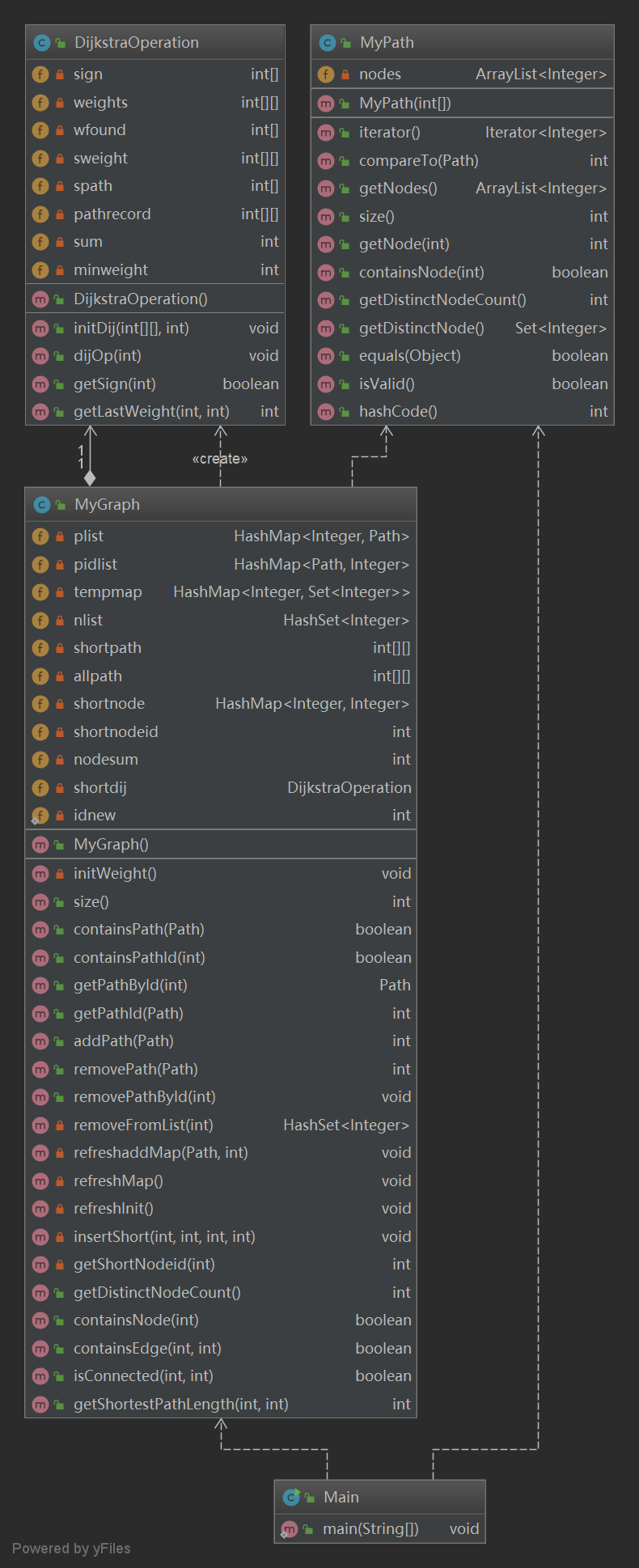
• 主要度量图

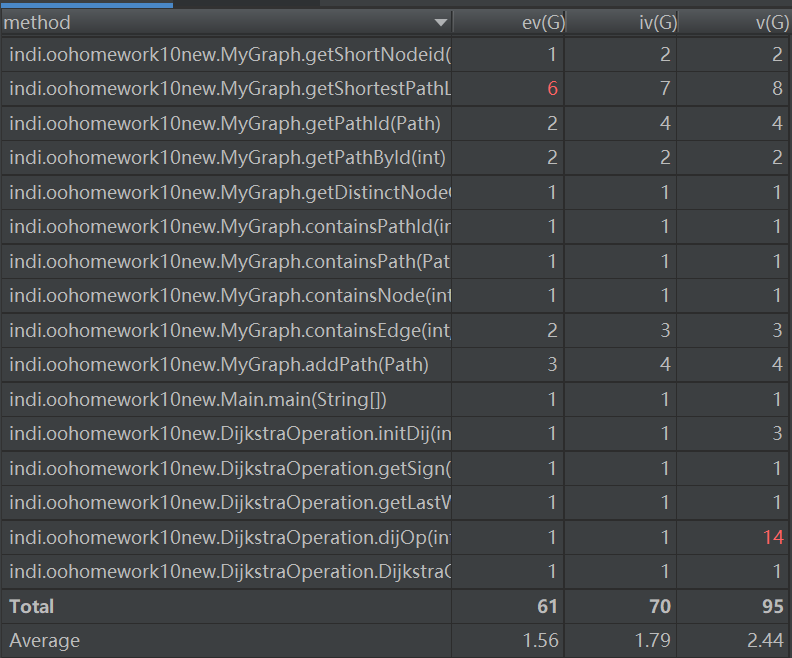
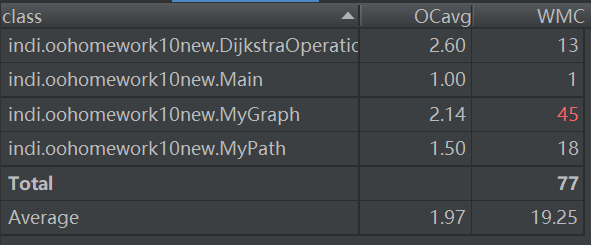
• bug分析

  在这一次作业中，我犯了一个致命性的错误，在算法的选择上没有清晰的认识，导致自己没有用现成的算法，而是使用了自己所想的龟速算法，每次查找都遍历了所有的边，导致TLE成为了必然。在bug修复中，我将算法改为了dijkstra算法，结果轻松地过了之前TLE的点。（上面的图为修改后代码的类图和主要度量图）

第三次作业

• 类图

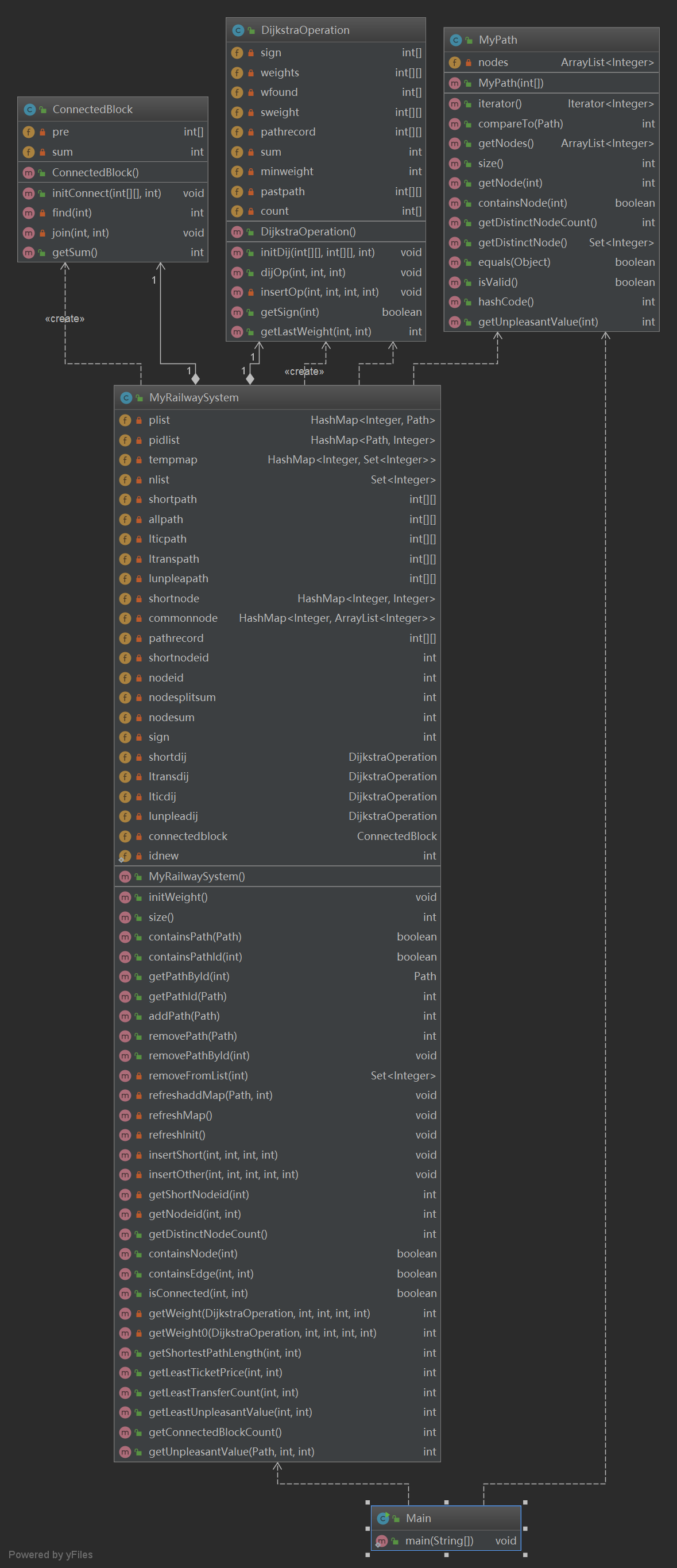
本次的架构是沿用上次的作业，使用dijkastra算法，并将四种查找综合为同一种，都当作为求最小权值的路径。

• 主要度量图

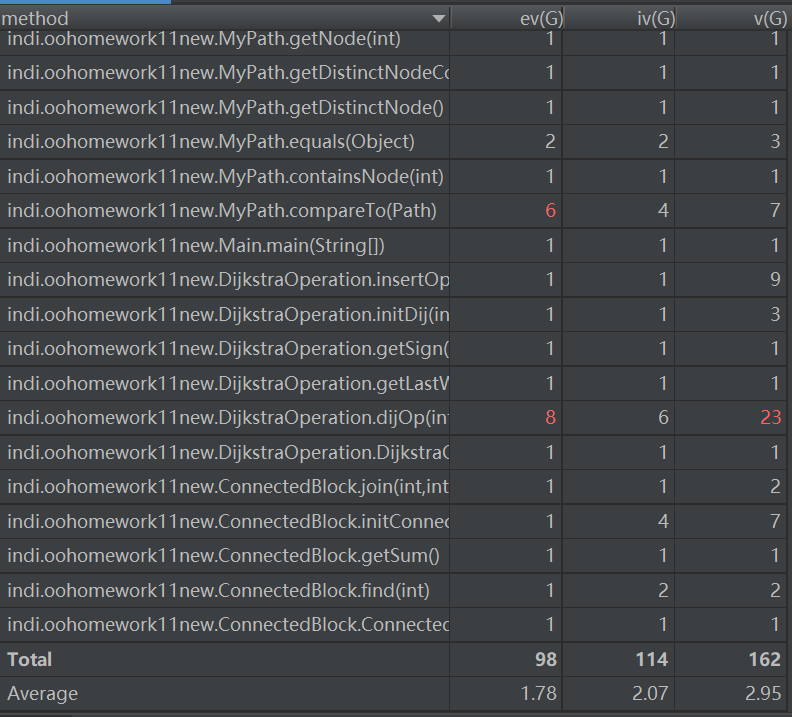
• bug分析

  自己的bug：

  这次作业我因为使用了不正确的拆点法而死的很惨。其实在最初写代码的时候，我已经意识到用我所想到的拆点法会需要比较大的数组，但是由于我想当然地以为测评机是实现很多如此大的数组，这点并没有引起我的注意，结果是我太天真，最终由于RE，又没有多少时间进行重构，导致最后只能改小数组来通过中测，但是这也使我强测发生了爆栈的问题。

  最后在bug修复的时候，我改了一种方法，将拆点法改为了不拆点的方法，并借鉴讨论区大佬和身边大佬的方法，将同一条路径中的点两两相连，这样它们之间的权值就可以直接加上换乘时需多加的权值，之后再进行dij算法查找最小权值的边，最后结果在减去各个情况换乘需加上的权值（因为之前都加了一遍）。这种方法可以完美避开了使用dij算法时易出现的找不到最优解的情况。

  他人的bug：

  在测试他人的bug，发现大家主要错的还是两点：一种情况是算法不够优化，速度过慢导致TLE；另一种情况是在查找最小权值路径时，发生了隐形的错误，导致最后的结果不是最终情况。

---

对规格撰写和理解上的心得体会

这三次作业的理解和完成虽然并不是非常顺利，在数据结构和算法的使用上遇到了一些瓶颈，但是可以肯定的是，对于jml语言已经初步入门，能够基本地根据方法编写相应的JML规格和理解现有的JML规格。根据JML规格编写代码，我也体验到了真正面向对象编写程序的过程。虽然目前写的程序规模还比较小，JML还没有体现出很大的作用，但是当之后的代码量大的时候，使用JML可以使我们更快地定位到错误的地方，这就能对我这个经常debug无能的人提供很大的帮助。