SIGAI机器学习第二十四集 聚类算法1

讲授聚类算法的基本概念，算法的分类，层次聚类，K均值算法，EM算法，DBSCAN算法，OPTICS算法，mean shift算法，谱聚类算法，实际应用。

大纲：

聚类问题简介
聚类算法的分类
层次聚类算法的基本思想
簇之间距离的定义
k均值算法的基本思想
k均值算法的流程
k均值算法的实现细节问题
实验
EM算法简介
Jensen不等式
EM算法的原理推导
收敛性证明

聚类算法是无监督学习的典型代表，前边讲过的数据降维算法是无监督学习的另外一种典型代表。

聚类问题简介：

聚类算法的概念第四讲机器学习的基本概念里边已经讲过了，聚类算法是没有训练过程的，也没有标记好标签的那种样本，它本质上也是一种分类问题，但是他没有训练过程，它是无监督的。

它是完成这样一个任务，将样本集划分成多个类，保证同一类的样本之间尽量相似，不同类的样本之间尽量不同，什么是相似什么是不同解释有好多种，没有严格的定论，因此诞生了各种不同的聚类算法。

在分类里边每种类型为一个类class，在聚类算法里边为了把它区分开来，我们称它为一个簇cluster。簇在计算机科学里边是经常被使用的，比如操作系统、文件系统，硬盘的磁盘它就是以簇为单位的，几个block做成一个簇。

需要强调的是聚类算法它是没有训练过程的，直接完成对一组样本的划分，比如说，加入搜索引擎抓了一万篇网页，现在把它自动分成类，归类归好，完成这样一个归类，归类的类型可能有军事、科技、政治、娱乐、体育等等，事先没有告诉我们的算法有哪些类，只是把它归类归好，按照我们的常识它就那些类型，算法自动发现这样一些类把样本划分开来，这就是聚类算法。再比如有一堆水果包括桃子、杏、梨等，由于是无监督的，算法要自动把他们认出来，保证发现里边的类型即簇这个东西，保证同一个类型它尽可能的是相似的。如果是有监督的分类算法它是不一样，它是先拿很多样本让你学习一遍，然后人工给标好了类型标签，训练得到一个模型，分类的时候是用这个模型对样本进行判断。这是他们之间的一个本质不同，分类算法它是有训练样本来训练并得到一个模型，用这个模型来预测，而聚类算法是没有这样一个过程的，只是给你一堆水果，让你自动把它分开。

聚类算法是无监督学习的两类典型代表之一，一类是数据降维问题，还有一类就是聚类问题， 前边都是一个直观的定义，如果给聚类算法下一个严格的定义：

它的本质就是集合的划分，给定一个样本集C={x1,...,xl}（这里边是没有样本标签纸y的），聚类算法要将其划分为多个不相交的子集C1,...,Cm（具体m取多少是不一定的，可能是人工指定的，也可能是算法自动发现的），划分成这么多子集是有要求的，首先 这些子集的并集是整个样本集C1∪C2...∪Cm=C（即它是C集合一个完整的划分，不可能存在一个 样本它不属于任何一个子集，后边的opstic等算法可以算法噪声样本，但是你可以把噪声也归结为一类样本，总之一个样本要有类别归属的），然后每个样本只能属于一个子集Ci∩Cj=Ø(i≠j)（这种称为硬聚类算法，软聚类算法是一个样本它可能属于第一个类也可能属于第二个类也可能属于第三个类，它属于每个类它有一个概率值，如果不做特殊说的话，后边所指的所有的聚类算法都属于硬聚类算法）。

集合的划分典型的就属于NPC(NP难)问题，可以这样直观的理解，它所有不同的划分情况随着集合C的规模l成指数级爆炸增长的，l很大的时候相当于l的多少次方，它既然有那么多的划分情况，要把所有的情况列出来看哪种情况是最优的这显然是不现实的，从理论上来说，我们也可以定义一个代价函数，比如说叫L()，对应这样一个划分规则我们算一个损失函数值，我们让这样一个损失函数值达到最小的时候对应的那个划分就是最优化分，这样虽然从理论上说是可行的，但是实际操作的时候不可行的，原因就是总共的可能划分它是呈指数级增长的规模，所以说不可能把它全部列举出来。

聚类算法的分类：

因为没有人工定义的类别标准，因此要解决的核心问题是如何定义簇，如果定义了簇就确定了集合的划分，怎么定义簇呢？通常的做法是根据簇内样本间的距离和样本点在数据空间中的密度（虽然说）来确定。对簇的不同定义导致了各种不同的聚类算法。

常见的聚类算法：
①连通性聚类。典型代表是层次聚类，其实它就是用了样本之间的距离的思想，如果两个样本之间距离很近的话他们就属于同一个簇，如果两个样本离的很近说明他们是联通的，根据样本之间的联通性构造簇，所有联通的样本属于同一个簇。
②基于质心的聚类。用一个中心来表示一个簇，把每个样本分到离他最近的最近的中心所代表的那个簇里边去，典型代表是k均值算法，它用类中心向量来表示这个簇，样本所属的簇由它距离每个簇的中心距离而定。
③基于概率分布的聚类。假设每种类型的样本服从某一概率分布，如多维正态分布，典型代表是EM算法。
④基于密度的聚类。根据样本的密度来确定簇的思想，样本分布比较密集的一块东西就是一个簇，分布比较稀疏的认为是噪声点根本就不是簇，它的核心就是计算每个样本它所处的位置在空间中的密度把密度大的区域给找出来最后形成簇，典型代表是DBSCAN算法，OPTICS算法，以及均值漂移（Mean shift）算法，它们将簇定义。
为空间中样本密集的区域
⑤基于图的算法。和深度学习里边的拉普拉斯特征映射有点像，把样本点看作图的顶点构造出一个图来，通过对图的切割就把一个图切割成不同的子图然后来完成这样一个聚类，它的典型的代表是谱聚类算法，用样本点构造出带权重的无向图，每个样本是图中的一个顶点，然后使用图论中的方法完成聚类。
层次聚类算法的基本思想：

对于有些问题，类型的划分具有层次结构，像水果，分为苹果、梨、桃子等，然后苹果又分为蛇果、黄元帅等，桃子又分为水蜜桃、黄桃等。
初始时每个样本为一个簇，然后计算任意两个簇之间的距离，将距离最近的两个簇进行合并反复合并，反复执行这种操作，最后形成一棵树。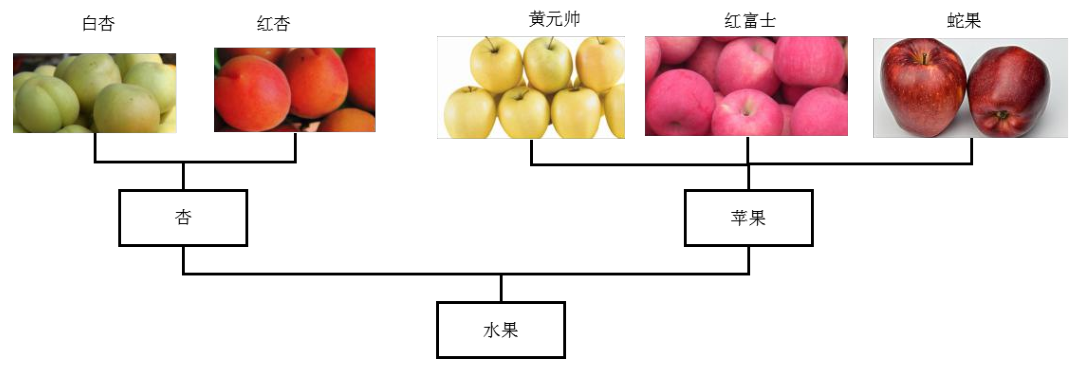

簇之间距离的定义：

层次聚类是反复的把两个距离最近的簇合并掉形成一个簇，怎么定义两个簇之间的相似度呢或者说他们之间的距离？簇之间的距离定义有这么几种常见的方法：

任意两个样本之间距离的最大值：

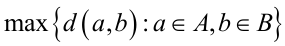
任意两个样本之间距离的最小值：

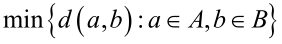
所有样本距离之间的均值：

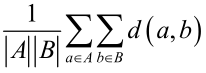
可以看到，层次聚类它实现起来是非常简单的，但是他的计算复杂度是相当的高的，无论用哪种距离，最后都要遍历A、B集合所有的距离对。

k均值算法的基本思想：

k均值算法，它是一种迭代法，他和前边讲的求解高斯混合模型的EM算法是有密切的联系的，可以看成是一种特例。

这种算法需要人工的指定一个参数k，你要把样本聚成多少个类是需要人工指定的，当然后边也发展了一些这个算法的变种它能自动的确定这个k的值，我们这里不讲变种算法。

这个算法要达到的目标是将整个样本集划分为k个子集，他要满足两个要求即这k个子集的并集是总的样本集和任意类的交际为空。每个簇用一个中心点向量μi=1/lΣxj表示，这个算法本质上是求解这样的一个问题：把每个样本分到离它最近的那个类中心μi所代表的类里边去，也就是说让每个簇里边的样本和它的中心的距离平方和最小化，其实类似于方差。

将样本划分到离它最近的簇（簇中心），而簇中心又依赖于样本的划分结果：

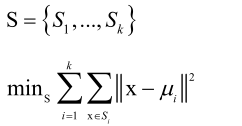
x属于某个簇它是依赖于μ的，而μ又依赖于x属于某个簇，这是一个循环的依赖关系，因此我们实现的时候要把它打破掉，后边讲怎么做。

把S划分为k个子集S1、S2、...、Sk，它是呈指数级爆炸的情况，所以说这个问题是一个NP难的问题，没法直接求它的全局最优解，k的规模、样本个数很大的时候只能近似求解。

k均值算法的流程：

计算μ是依赖于每个样本x它是属于哪个类的，而x属于哪个类它又依赖于μ，这里边有一个循环依赖的关系，我们要打破这种循环依赖，怎么打破呢？

假设k个类(簇)它的中心向量已经知道了，给它一个初始的猜测值，之后呢就开始迭代了一直到收敛为止，收敛的判断准则是各个类的μ它的两次迭代之间变化非常小了。每次迭代分两个步骤，分配（把每个样本分配到离他最近的簇里边去，计算每个向量xi和每个类μj之间的距离，把它分配到最近的那个μ里边去就可以了），然后根据这个分配方案重新更新每个簇的中心向量μ（把属于每个类的向量xi加起来除以它的样本数，然后得到中心向量）。

是怎么打破的这个的这个环呢？刚开始给μ一个初始的不太靠谱的猜测值，然后切进来这个环开始转，直到最后收敛到最优解上边去。

k均值算法的实现细节问题：