Kotlin泛型与协变及逆变原理剖析

在上一次https://www.cnblogs.com/webor2006/p/11234941.html中学习了数据类[data class]相关的知识，这次会学习关于泛型相关的东东，其中有关于泛型我经常不太理解的关于<? extends T>和<? super T>的使用方式，所以好好学习，天天向上。

密封类（sealed class）:

关于这个类，我们在上一次学习中其实是提到过这个关键字，回忆一下：

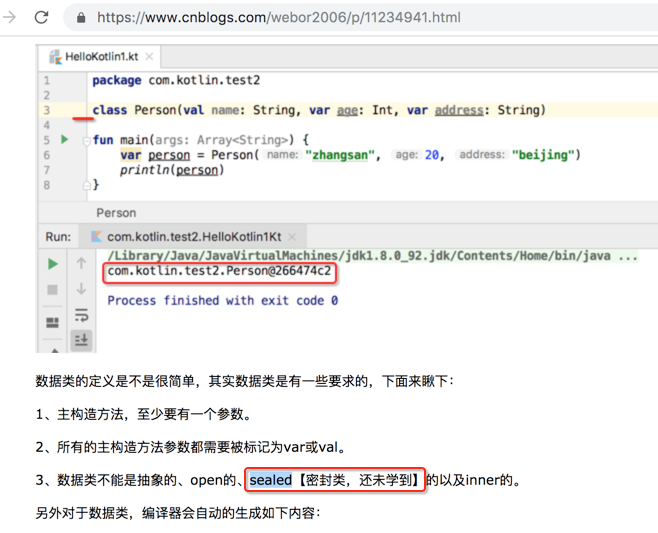
所谓密封，就是将东东给包装起来，然后我们要使用只能使用包装好里面受限的东东，其实跟Java的枚举很类似，但又跟枚举不太一样，其实它是枚举的一个扩展，枚举我们知道在定义时其实例就已经规定好了，关于密封类跟java枚举的区别等学会了用密封类之后就能体会到了 ，而密封类其实描述的是类的一种层次，也就是父类和子类的一种关系，而密封类的子类可以有多个，说了这么说那也不知道在说啥，直接来撸码来看下密封类是个什么东东，在撸码之前先明白个规则：

1、在Kotlin中如果一个密封类有若干个子类，那么密封类和子类必须定义在同一个文件当中，其中在Kotlin1.1版本之前对于它的规定更加的严格，当时是要求密封类的子类必须要定义在密封类里面，而在Kotlin1.1版本以后就打开了这个限定了。

2、在Kotlin中，密封类是一个抽象类，不能实例化。

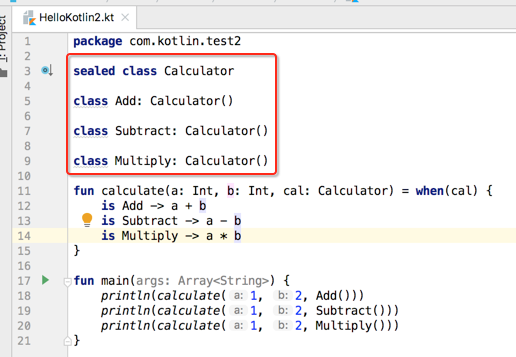
好，下面来定义一个密封类：

因为它是抽象的，所以可以定义几个子类，如下：

这样写貌似有点想写多态的感觉，肯定还得定义一个计算方法呗，下面定义一下：

下面来调用一下：

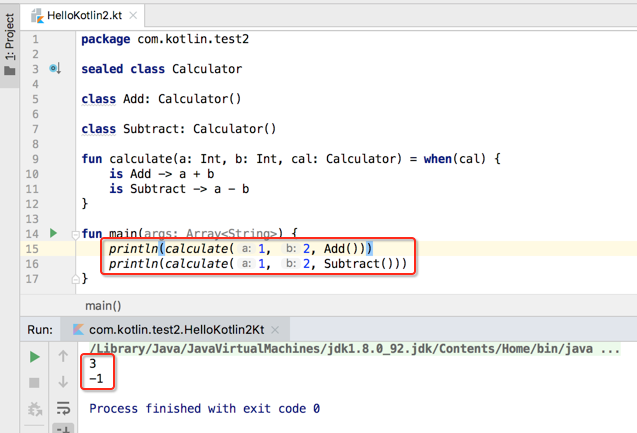
貌似跟枚举使用没啥太大的区别，好，接下来再来定义一个子类区别就可以显现了，如下：

看懂了密封类的作用木有，也就是它就是描述一种类的层次关系，目前我们密封类定义了三个子类，而when表达式的条件也必须有三种可能，而Java中的枚举是没有这一层关系的，下面来修改一下程序：

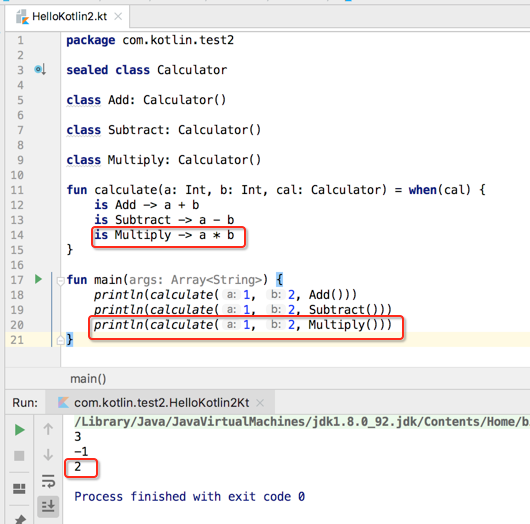
也就是用了密封类之后，我们在用when表达式时就可以不用else分支了，假如我们强行加上else则IDE会报冗余提示：

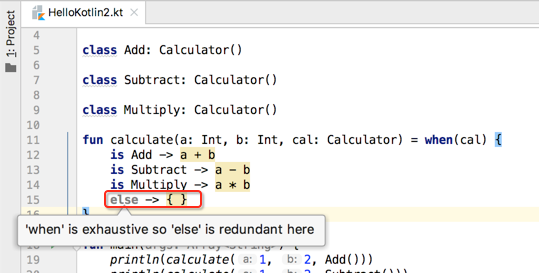
可以看一下我们的密封类和子类是定义在了一个文件当中，符合之前说的规定：

而如果说我们再定一个类，来继承密封类的子类，那就没有这个“必须定义到一个文件里”的限制了。

泛型(generics)：

关于泛型是啥，用一句描述是：表示变量类型的参数化，其语法跟Java类似，如下：

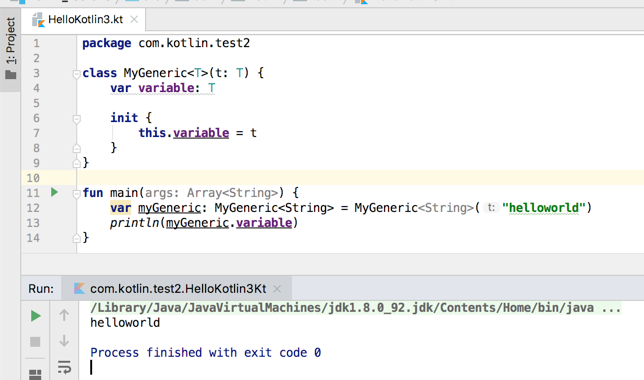
上面泛型是一个完整的使用方式，其实可以精简一下，利用Kotlin的推断机制，如下：

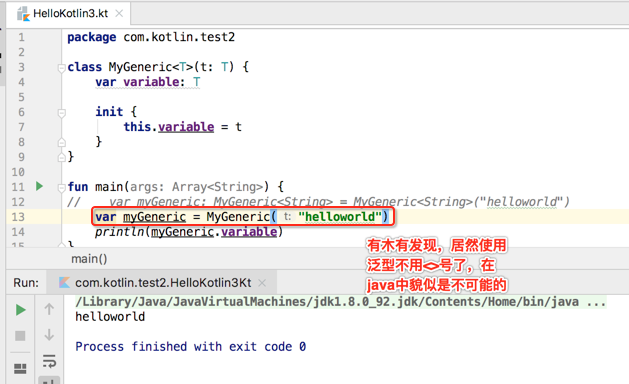
协变[covariant]与逆变[controvariant]原理剖析：

关于泛型的使用其实很简单，但是！！如文章开头所说，一直理解不了在Java框架中很多使用泛型都会用<? extends T>和<? super T>，像Rxjava中：

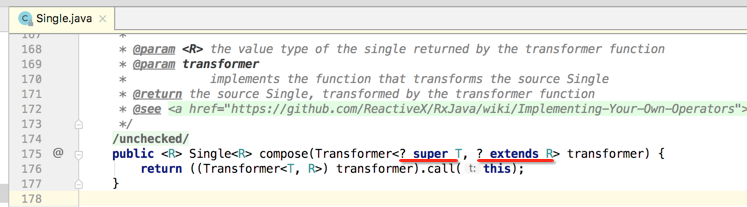
所以这次抛开语言层面来对泛型这块的东东彻底把它搞清楚，也就是关于泛型的协变与逆变的概念，下面先从Java的具体泛型的示例中来开始一点点理解它：

一切很自然，但是！！！我们不能这样做：

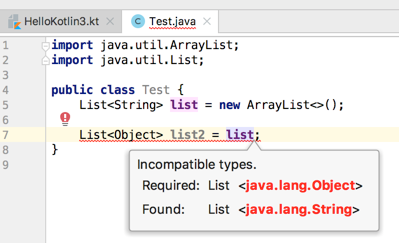
这是为啥呢？假设这个等式成立的话，那可以这样写：

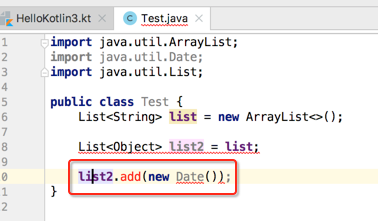
由于list2指向了list，那么我可以以list的角度来取数据，那么就会有：

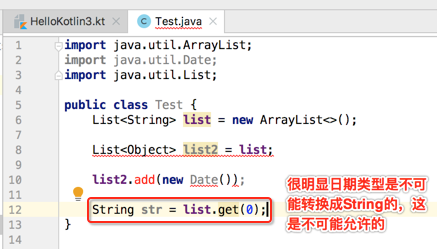
为了解决这样的问题，Java提供了通配符，如下：

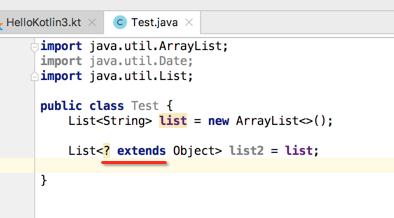
下面再以集合为例对其进行说明：

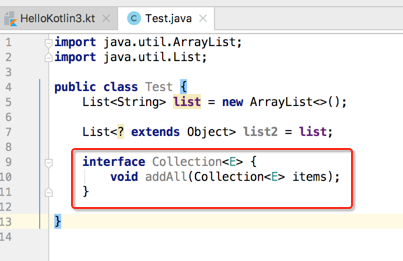
集合接口中定义了一个addAll()方法，可以添加现已经存在的集合， 下面定义一个添加方法：

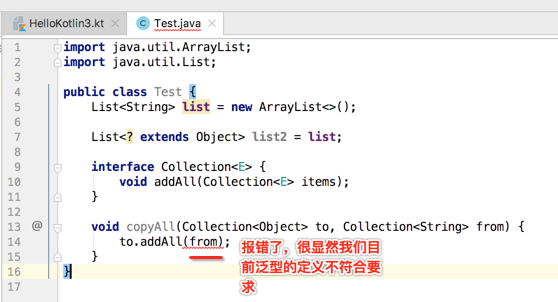
很显然此添加方法在实际需求中是很常见的，这里就可以瞅一下JDK自带的Collection.addAll()方法的定义：

所以咱们校仿一下：

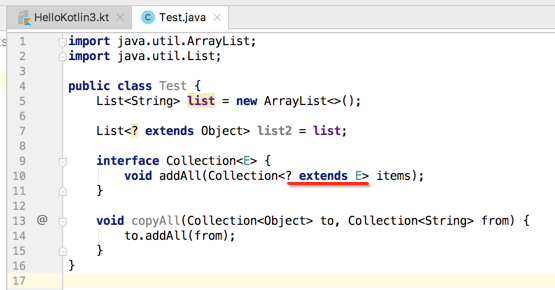
这样的话，我们就可以很安全的当E类型从集合中去读取，也就是会当Object的类型来读取，所以Collection<String>是Collection<? extends Object>的子类型，这种情况就叫做协变，它只会从集合中当成Object来读取元素，协变是针对读取的；而相反如果这样写的话则是逆变，逆变是针对写入的，如下：

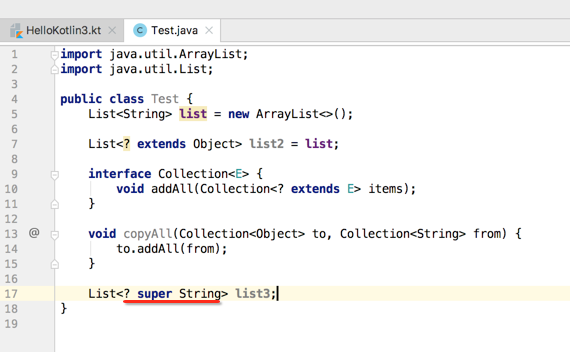
也就是往集合中写元素时必须是String以上的类型，另外需要明白：我们如果只从中读取数据，而不往里面写入内容，那么这样的对象叫做生产者，也就是协变，此时使用 ? extends E；如果只向里面写入数据，而不从中读取数据，那么这样的对象叫做消费者，也就是逆变，使用? super E。貌似看标的这句话跟预想的理解有点出入，反正先记住这个结论。

下面来看一下在Kotlin中如何来解决协变和逆变的问题，如下：

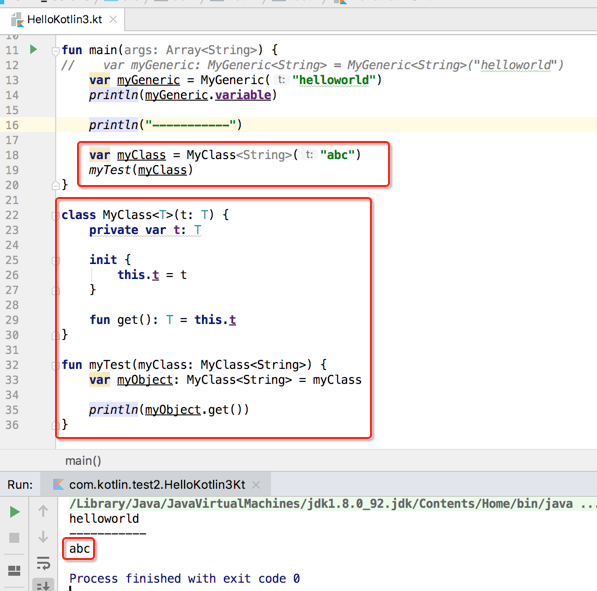
一切如预期，接下来要改动程序了：

此时可以看到我们定义的泛型，在整个类中只有读取，没有写入，如下：

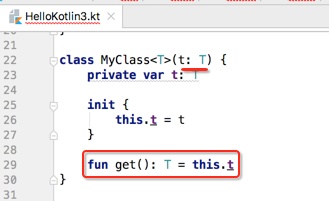
这其实是协变，这时如果在Java中就可以声明为? extents T，但是在Koltin中用它来表示协变：

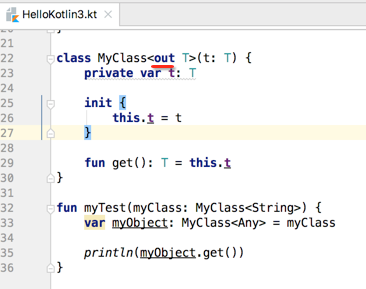
这样就比Java直观，表示该泛型是要被读的，那如果给T增加一个写方法呢？

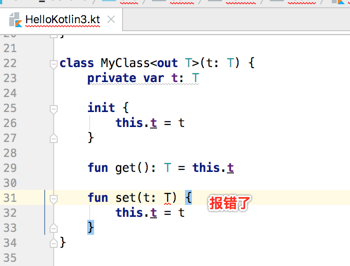
提示如下：

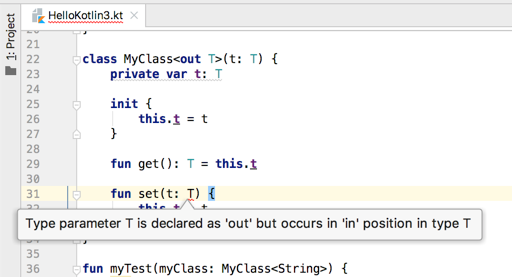
所以可见对于协变只能用到读，接下来定义一个逆变：

而由于Int的父类是Number，如下：

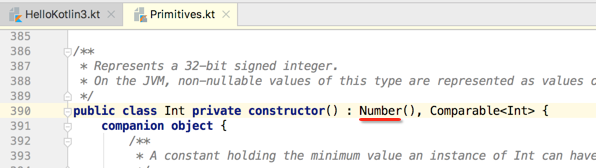
所以咱们改一下程序：

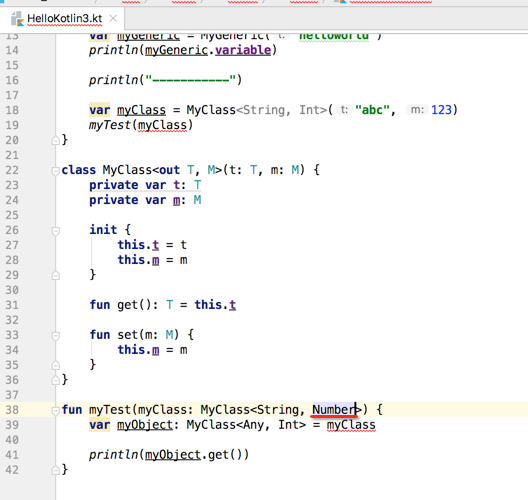
此时对应的也得改一下调用：

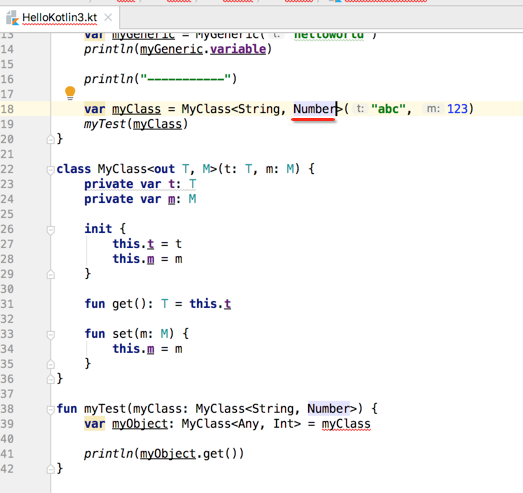
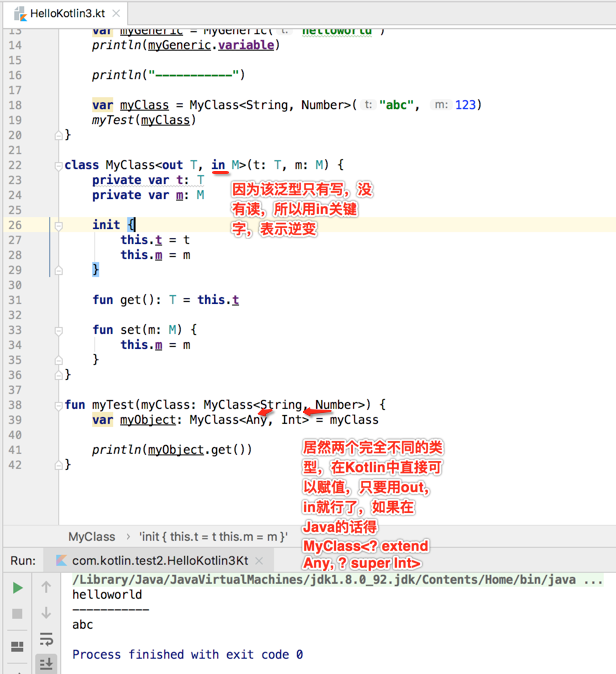
此时报错了，这里就可以加上in逆变关键字，如下：