matlab的拟合函数polyfit()函数

matlab的多项式拟合：

polyfit()函数

功能：在最小二乘法意义之上，求解Y关于X的最佳的N次多项式函数。

clc;clear;
close all;
x=[                ];
y=[2.7    7.4    20.0    54.5    148.4];
r=corrcoef(x,y) ;%两个变量的相关系数
a=polyfit(x,y,)
x1=:0.1:;
P=polyval(a,x1);%a是多项式拟合后返回的系数
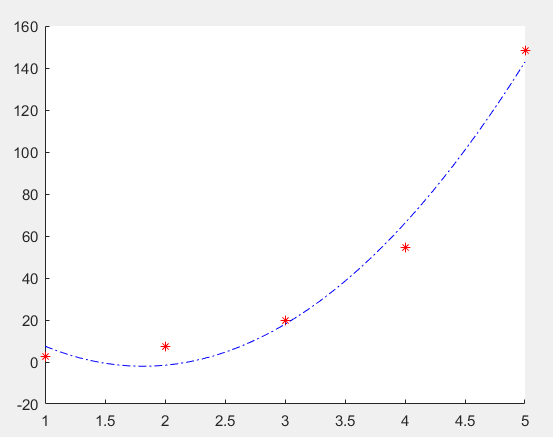
figure();hold on;plot(x,y,'r*',x1,P,'b-.');

注：a是返回的两次多项式的系数，返回结果是：14.3071  -51.9929   45.2000，这意味着拟合的多项式是：

y=45.2000+（-51.9929）*x+14.3071*x^2

clc;clear;
close all;
x=[                ];
y=[2.7    7.4    20.0    54.5    148.4];
r=corrcoef(x,y) ;
%a=polyfit(x,y,)
b=polyfit(x,y,)
c=polyfit(x,y,)
x1=:0.1:;
%Pa=polyval(a,x1);%a是多项式拟合后返回的系数
Pb=polyval(b,x1);%a是多项式拟合后返回的系数
Pc=polyval(c,x1);%a是多项式拟合后返回的系数
%figure();hold on;plot(x,y,'r*',x1,Pa,'b-.');
figure();hold on;plot(x,y,'r*',x1,Pb,'r-.');
figure();hold on;plot(x,y,'r*',x1,Pc,'g-.');

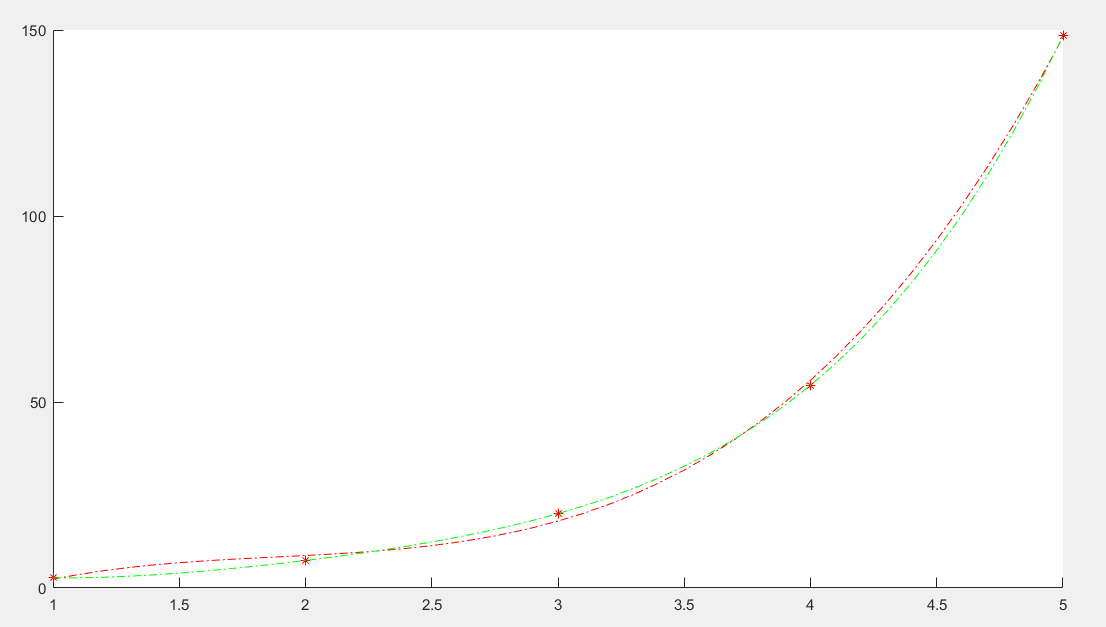
注：红色是三次拟合的结果。

绿色是四次拟合的结果。

例1：

clc;clear;
close all;
x=[                ];
y=[2.7    7.4    20.0    54.5    148.4];
r=corrcoef(x,y) ;
%a=polyfit(x,y,)
[b s]=polyfit(x,y,)
%c=polyfit(x,y,)
x1=:0.1:;
%Pa=polyval(a,x1);%a是多项式拟合后返回的系数
Pb=polyval(b,x1);%a是多项式拟合后返回的系数
%Pc=polyval(c,x1);%a是多项式拟合后返回的系数
%figure();hold on;plot(x,y,'r*',x1,Pa,'b-.');
figure();hold on;plot(x,y,'r*',x1,Pb,'r-.');
%figure();hold on;plot(x,y,'r*',x1,Pc,'g-.');

注：[b s]=polyfit(x,y,3) %这里返回的s是个结构体，s中的normr表示拟合的残差的二范。

---

以下例子的来源：https://blog.csdn.net/qq_33591755/article/details/82453757

有如下数据

时间t	1900	1910	1920	1930	1940	1950	1960	1970	1980	1990	2000
人口y	76	92	106	123	132	151	179	203	227	250	281

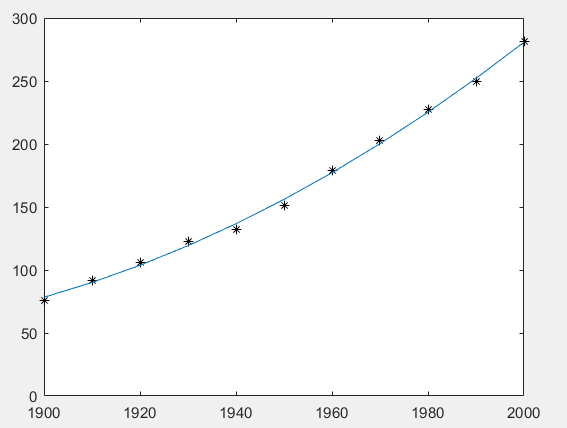
1. y与t的经验公式为 y = at^2 + bt + c

clear;
clf;                                                      %清除当前窗口
clc;
t = ::;                                         %时间t
y = [          ];          %人口y

plot(t,y,'k*');
hold on;
% figure;       　　　　　　　　　　　　　　　　　　　　　　　　  %重新开一个图
p1 = polyfit(t,y,);
h=polyval(p1, t);
plot(t, h);
axis([   ]);                                  %图像xy轴范围

disp(char(['y=',poly2str(p1,'t')],['a=',num2str(p1()),'   b=',...
    num2str(p1()),'   c=',num2str(p1())]));

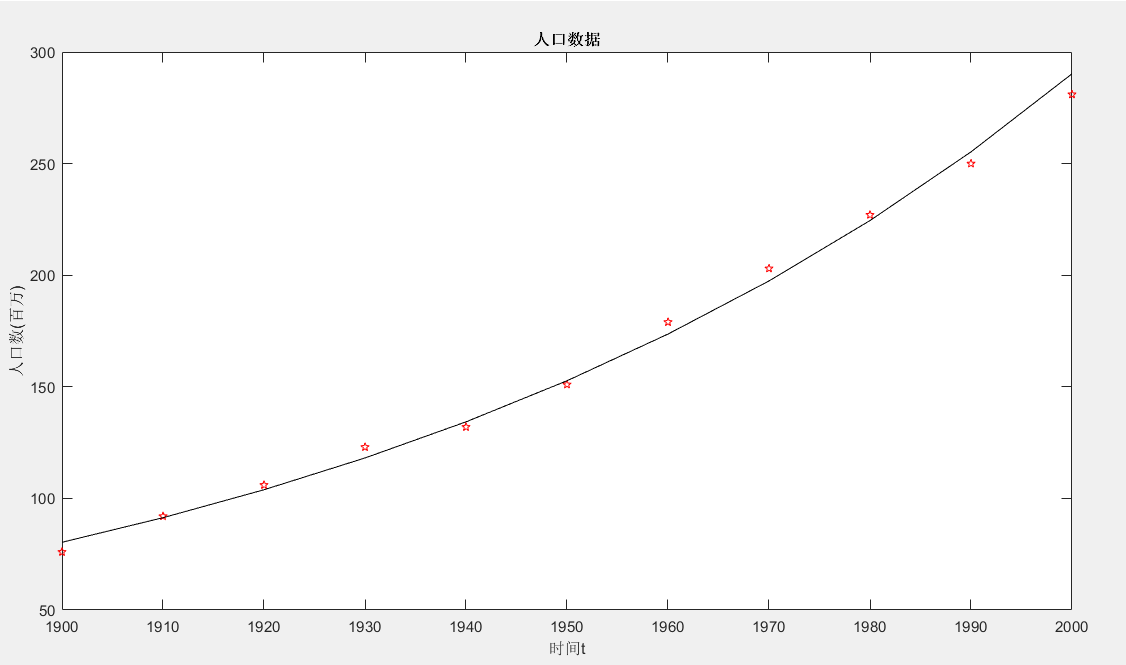
2. y与t的经验公式为y = a e^(bt)

clear;
clf;                                                      %清除当前窗口
clc;
t = ::;                                         %时间t
y = [          ];          %人口y
yy = log(y);                                              %指数基尼必需的线性化变形
p2 = polyfit(t,yy,);
b = p2();
a = exp(p2());
y2 = a * exp(b*t);                                       %指数拟合函数式
plot(t,y,'rp',t,y2,'k-');
grid off;
xlabel('时间t');
ylabel('人口数(百万)');
title('人口数据');

---

最佳拟合次数的确定：

clc;clear;
close all;
x=[                ];
y=[2.7    7.4    20.0    54.5    148.4];
for i=:
    y2=polyfit(x,y,i);
    Y=polyval(y2,x);%计算拟合函数在x处的值。
    if sum((Y-y).^)<0.1
        c=i
        break;
    end
end