【洛谷P3369】普通平衡树——Splay学习笔记（一）

二叉搜索树（二叉排序树）

概念：一棵树，若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树（baidu百科）。

就是一棵二叉树，所有的节点都满足：左子树内每个的点的值比当前点值小，右子树内每个的点的值比当前点值大

如下图

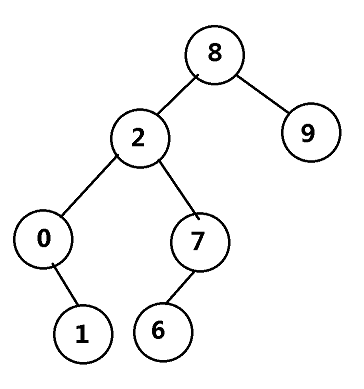
我们只需在树上中序遍历就会得到一个上升的权值序列

我们可以在二叉搜索树上干很多事情，比如插入某个值，查询第k大值，查询某个数的排名等，显然单次操作最坏复杂度为树的深度，如果树呈链状，它的复杂度就会爆炸

这时我们就要想办法保证二叉树的深度不会很大，最好是\(log\)级别的

平衡树

概念：一棵树，它是一棵空树或它的左右两个子树的高度差的绝对值不超过\(1\)，并且左右两个子树都是一棵平衡二叉树（baidu百科）

不用管上面在BB啥，大概就是一棵深度为\(log\)（节点数）的二叉搜索树

平衡树有很多维护方式，这里介绍的是\(Splay\)

\(Splay\)

变量

维护一棵Splay，最基础的变量有：

root     //根的编号

ch[N][2]    //每个结点的两个儿子

f[N]    //每个结点的父亲

cnt[N]    //相同权值的点会被插入到同一个结点上，这里维护当前权值的结点上的点的个数

val[N]    //每个结点的权值

size[N]    //每个子树的大小

题目保证权值不同时 cnt数组就没有用了

有时候 val、size数组也不需要开

旋转

\(Splay\) 最核心的操作就是旋转

旋转就是把一个点搞到它父亲的位置，同时要保持二叉搜索树的性质，如下图

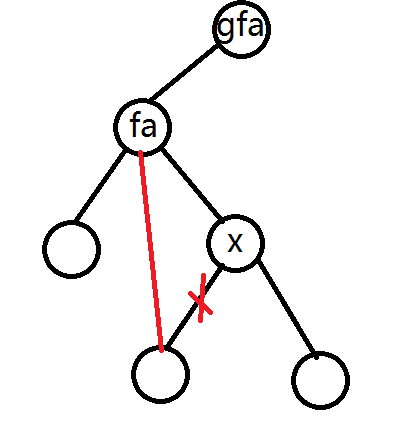
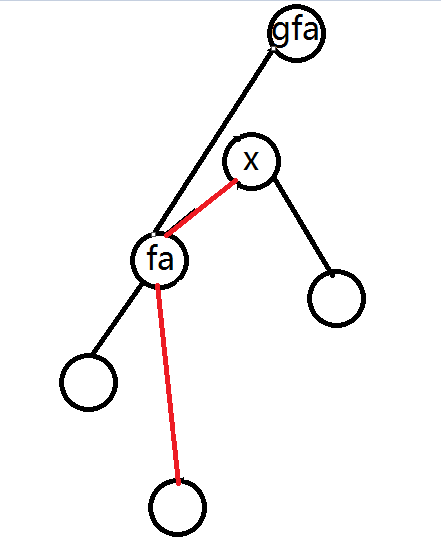
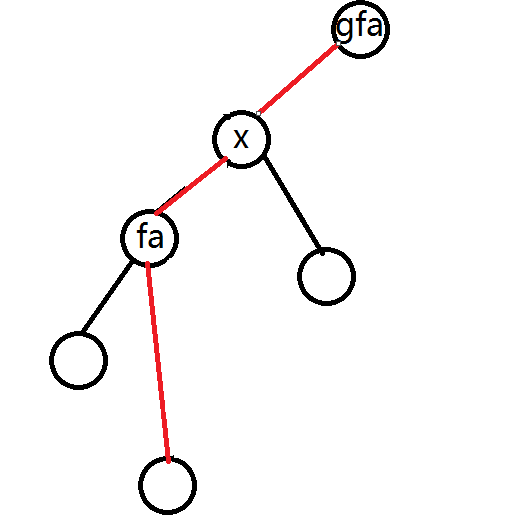
代码：

inline int get_w(int x){      //判断是x是f[x]的左儿子还是右儿子
    return ch[f[x]][1]==x;    //左儿子return 0，右儿子return 1
}

inline void push_up(int x){    //维护size
    if(x) size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
}

inline void rotate(int x){
    int fa=f[x],gfa=f[f[x]],w=get_w(x);
    ch[fa][w]=ch[x][w^1]; f[ch[fa][w]]=fa;        //fa 与 x的儿子 的关系
    ch[x][w^1]=fa; f[fa]=x;                           //fa 与 x 的关系
    f[x]=gfa; if(gfa) ch[gfa][ch[gfa][1]==fa]=x;    //x 与gfa的关系
    push_up(fa); push_up(x);                    //fa在x的下面，先push_up(fa)
}

\(splay\) 操作

即不断地旋转一个结点，把它转到根，以方便对它操作

如下图

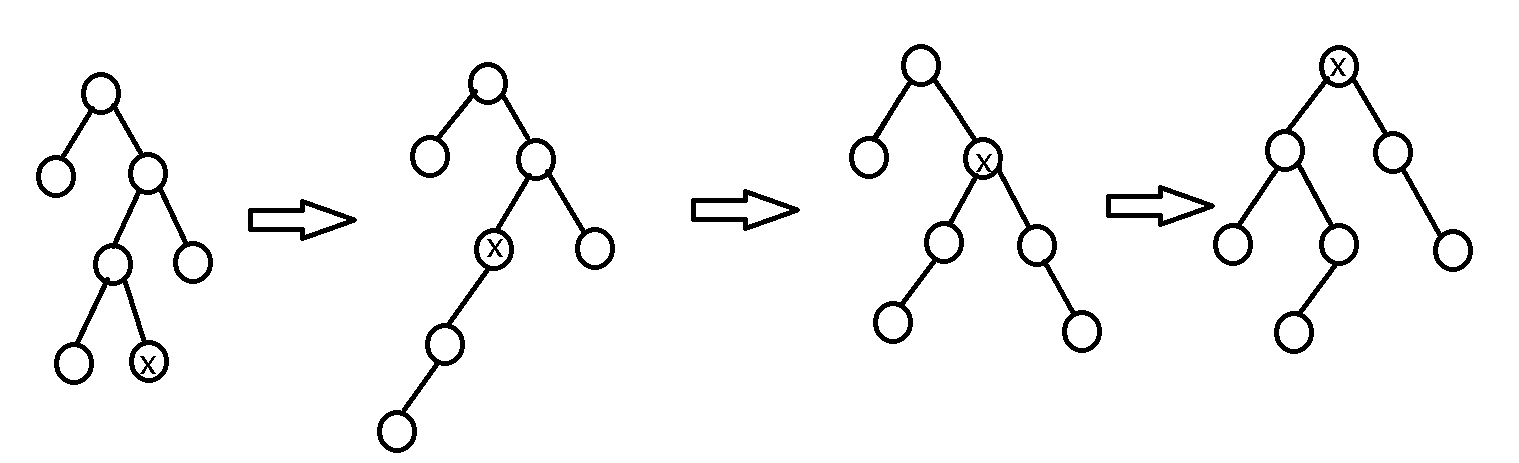
虽然它的深度没有变化我们成功把x搞到了根的位置

但是如果是一个这种形状：

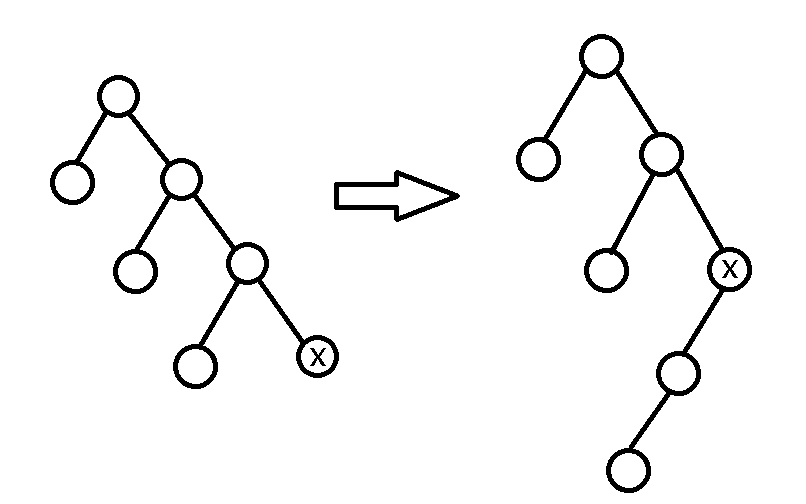
它就会非常丑

如果在\(x\)、\(fa\)、\(gfa\)在一条线上时，旋转\(fa\)就比较好看了

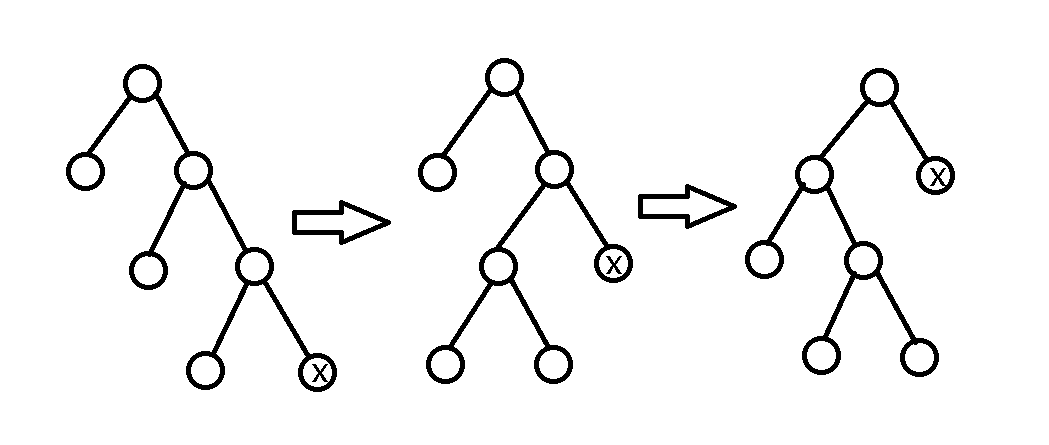
然而这里\(x\)转到根上最后深度还是会变大。。这个例子不是很好。。表在意这些细节

总之这么写就对了

inline void Splay(int x){
    for(int fa;fa=f[x];rotate(x))
        if(f[fa]) rotate(get_w(x)==get_w(fa)?fa:x);
    root=x;
}

剩下的操作就比较好理解了

\(insert\)

插入一个点，如果\(Splay\)中有相同权值的结点，最就会在这个结点上\(cnt+1\)；

如果没有相同权值的结点，就会插入到一个叶子结点上

具体看代码：

void insert(int x){
    if(!root){        //Splay为空，直接设为根
    	val[root=++Size]=x;
        size[Size]=cnt[Size]=1;
        return;
    }
    int now=root,fa=0;
    while(1){
        if(val[now]==x){        //权值相同，直接++cnt[now]
            ++cnt[now]; push_up(now);
			push_up(fa); Splay(now);    //最后把now splay到根是因为插入x后，从根到now的路径上的结点size都需要更新
			return;
        }
        fa=now;now=ch[now][x>val[now]];    //根据权值判断向左儿子/右儿子走
        if(!now){        //到达叶子结点
            f[++Size]=fa;val[Size]=x;
            size[Size]=cnt[Size]=1;
            ch[fa][val[fa]<x]=Size;
            push_up(fa);Splay(Size);        //Splay(Size) 和上面一样
			return;
        }
    }
}

\(find\_num\)

查找\(Splay\)中\(rank=x\)的\(num\)

int find_num(int x){
    if(!root) return 0;
    int now=root;
    while(1){
        if(x<=size[ch[now][0]]) now=ch[now][0];    //左子树的大小等于x或者比x大，那么rank为x的数一定在左子树中
        else{
            int temp=size[ch[now][0]]+cnt[now];
            if(x<=temp) return val[now];        //左子树的size+cnt[now]>=x,rank为x的点在now上
            x-=temp; now=ch[now][1];        //rank为x的点在右子树中，在右子树中rank为x-temp
        }
    }
}

\(find\_rank\)

查找\(Splay\)中\(val=x\)的点的\(rank\)

int find_rank(int x){
    if(!root) return 0;
    int now=root,ans=0;
    while(1){
        if(x<val[now]) now=ch[now][0];        //val=x的点在左子树中
        else{
            ans+=size[ch[now][0]];              //不在左子树中，比左子树的所有结点权值都大，rank加上左子树的大小
            if(x==val[now]){
                Splay(now); return ans+1;    //now的权值就是x，返回rank，Splay(now)是为了方便下面的del操作
            }
			ans+=cnt[now],now=ch[now][1];    //往右子树找
        }
    }
}

\(find\_pre/suf\)

查找\(root\)的前驱结点

显然\(root\)的前驱结点就是\(root\)的左子树中权值最大的点

后缀结点同理

inline int find_pre(){
    int now=ch[root][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}

inline int find_suf(){
    int now=ch[root][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}

\(del\)

删除一个权值为\(x\)的点

流程：

先把权值为\(x\)的点\(splay\)到\(root\)，方便操作

若\(cnt>1\),直接\(--cnt\)

否则

若左儿子为空，直接把右儿子当做根即可

若右儿子为空，同理

否则

找到\(root\)的前驱，\(splay\)到根，

原先的\(root\)一定成了新\(root\)的右儿子，且原\(root\)没有左儿子

新\(root\)、原\(root\)、原\(root\)的右儿子构成一条链的结构，用类似于链表删除操作即可删除原\(root\)

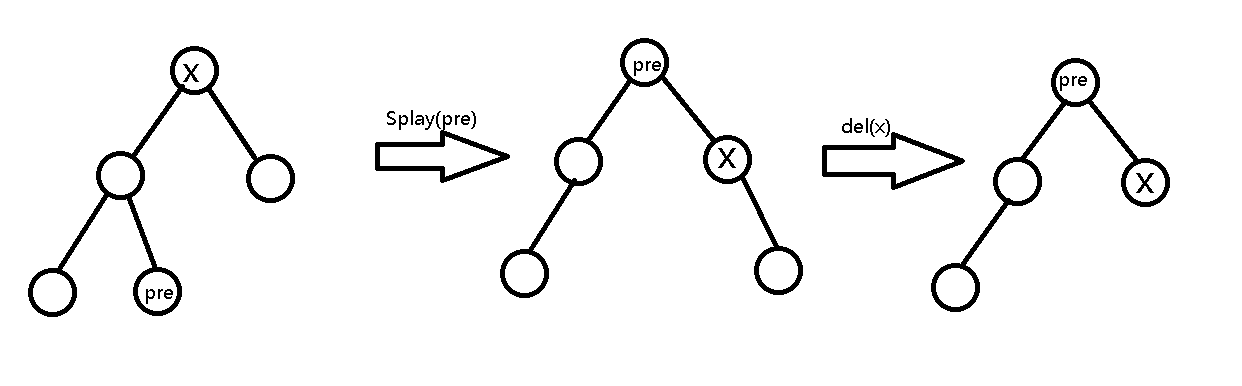
void del(int x){
    find_rank(x);    //找到权值为x的点并把它旋转到root
    if(cnt[root]>1){
        cnt[root]--; push_up(root);
		return;
    }
    if(!ch[root][0]*ch[root][1]){
    	root=ch[root][0]+ch[root][1];
        f[root]=0; return;
    }
    Splay(find_pre());
	ch[root][1]=ch[ch[root][1]][1];     //删除原root
    f[ch[root][1]]=root;push_up(root);
}

完整代码

#include<iostream>
#include<cstdio>
using namespace std;

const int MAXN=100010;

inline int read(){
    int x=0,f=1; char c=getchar();
    while(c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0')x=(x<<3)+(x<<1)+c-'0',c=getchar();
    return x*f;
}

int n,root,Size;
int ch[MAXN][2],f[MAXN],size[MAXN],cnt[MAXN],val[MAXN];

inline int get_w(int x){
    return ch[f[x]][1]==x;
}

inline void push_up(int x){
    if(x) size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
}

inline void rotate(int x){
    int fa=f[x],gfa=f[f[x]],w=get_w(x);
    ch[fa][w]=ch[x][w^1]; f[ch[fa][w]]=fa;
    f[fa]=x; ch[x][w^1]=fa; f[x]=gfa;
    if(gfa) ch[gfa][ch[gfa][1]==fa]=x;
    push_up(x); push_up(fa);
}

inline void Splay(int x){
    for(int fa;fa=f[x];rotate(x))
    	if(f[fa]) rotate(get_w(x)==get_w(fa)?fa:x);
    root=x;
}

void insert(int x){
    if(!root){
    	val[root=++Size]=x;
        size[Size]=cnt[Size]=1;
        return;
    }
    int now=root,fa=0;
    while(1){
        if(val[now]==x){
            ++cnt[now]; push_up(now);
			push_up(fa); Splay(now);
			return;
        }
        fa=now;now=ch[now][x>val[now]];
        if(!now){
            f[++Size]=fa;val[Size]=x;
            size[Size]=cnt[Size]=1;
            ch[fa][val[fa]<x]=Size;
            push_up(fa);Splay(Size);
			return;
        }
    }
}

int find_num(int x){
    if(!root) return 0;
    int now=root;
    while(1){
        if(x<=size[ch[now][0]]) now=ch[now][0];
        else{
            int temp=size[ch[now][0]]+cnt[now];
            if(x<=temp) return val[now];
            x-=temp; now=ch[now][1];
        }
    }
}

int find_rank(int x){
    if(!root) return 0;
    int now=root,ans=0;
    while(1){
        if(x<val[now]) now=ch[now][0];
        else{
            ans+=size[ch[now][0]];
            if(x==val[now]){
                Splay(now); return ans+1;
            }
			ans+=cnt[now],now=ch[now][1];
        }
    }
}

inline int find_pre(){
    int now=ch[root][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}

inline int find_suf(){
    int now=ch[root][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}

void del(int x){
    find_rank(x);
    if(cnt[root]>1){
        cnt[root]--; push_up(root);
		return;
    }
    if(!ch[root][0]*ch[root][1]){
    	root=ch[root][0]+ch[root][1];
        f[root]=0; return;
    }
    Splay(find_pre());
	ch[root][1]=ch[ch[root][1]][1];
    f[ch[root][1]]=root;push_up(root);
}

int main()
{
    n=read();
    int opt,x;
    while(n--){
        opt=read(); x=read();
        switch(opt){
            case 1: insert(x); break;
            case 2: del(x); break;
            case 3: printf("%d\n",find_rank(x)); break;
            case 4: printf("%d\n",find_num(x)); break;
            case 5: insert(x);printf("%d\n",val[find_pre()]);del(x); break;
            case 6: insert(x);printf("%d\n",val[find_suf()]);del(x); break;
        }
    }
    return 0;
}