【题解】PERIOD - Period [POJ1961] [SP263]

在进入这道题之前，我们需要了解 kmp 算法

不知道的童鞋可以去看一下Silent_EAG(一个可爱的女孩纸)的讲解。

关于 kmp 算法中 next 数组的周期性质

引理：

对于某一字符串 $S[1$～$i ]$，在它众多的$next[ i ]$的“候选项”中，如果存在某一个$next[ i ]$，使得: $i$ % $( i - next[ i ] ) == 0$ ，那么 $S[ 1$～ $( i -next[ i ] ) ]$ 可以为 $S[ 1$ ～ $i ]$ 的循环元而 $i / ( i - next[ i ] )$ 即是它的循环次数 $K$。

证明如下：

如图，$next[ i ] = j$,由定义得红色部分两个子串完全相同。

那么有$S[ 1$～$j ] = S[ m$～$i ]$ $( m = i - next[ i ] )$。

如果我们在两个子串的前面框选一个长度为 m 的小子串(橙色部分)。

可以得到：$S[ 1$～$m ] = S[ m$～$b ]$。

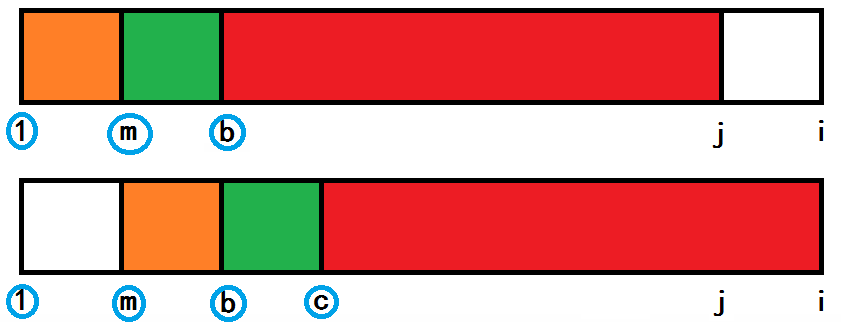
如果在紧挨着之前框选的子串后面再框选一个长度为 m 的小子串(绿色部分)，同样的道理，

可以得到：$S[ m$～$b ] = S[ b$～$c ]$

又因为：$S[ 1$～$m ] = S[ m$～$b ]$

所以：$S[ 1$～$m ] = S[ m$～$b ] = S[ b$～$c ]$

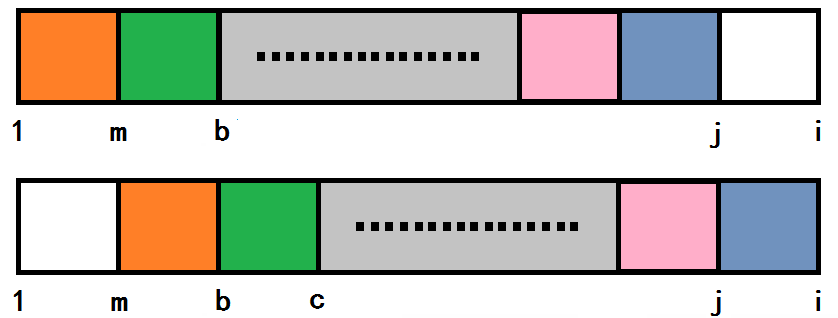
如果一直这样框选下去，无限推进，总会有一个尽头。

当满足 $i$ % $m == 0$ 时，刚好可以分出 $K$ 个这样的小子串，

且形成循环$( K = i / m )$。

因此我们需要从 $1$～$N$ 扫一遍，判断如果 $next[ i ]$

可以整除 $i$ ，即满足 $i$ % $( i - next[ ] ) == 0$ ，那么就可以

肯定$S[ 1$～ $( i - next[ i ] ) ]$是 $S[ 1$～$i ]$ 的最小循环元，而

$i / ( i - next[ i ] )$ 即是它的最大循环次数 $K$ ，直接依次输

出这些 $i$和 $K$ 即可。

那么为什么只判断 $next[ i ]$ 而不判断 $next[?]$呢？

（注：$next[i]$和$next[?]$表述的意义不同，为方便描

述，这里定义$next[?]$为$next[i]$的$“候选项”中的某一个）

实际上由这道题可以总结出很多结论：

结论一：

若$i-next[i]$可整除$i$,则$s[1$～$i]$具有长度为$i-next[i]$

的循环元，即$s[1$～$i-next[i]]$。(前面的一大堆文

字和图片已经给出了这个结论的证明，同时结论一

也是后面推导其他结论的理论基础）

结论二：

若$i-next[?]$可整除$i$,则$s[1$～$i]$具有长度为$i-next[?]$

的循环元，即$s[1$～$i-next[?]]$。

(用与结论一同样的证明方法可以推导出结论二)

(由此处可知，$i-next[?]$想用作循环元要满足的

条件是：$i-next[?]$可整除$i$)。

结论三：

任意一个循环元的长度必定是最小循环元长度的倍数

结论四：

如果$i-next[i]$不可整除$i$，$s[1$～$i-next[?]]$一定

不能作为$s[1$～$i]$的循环元。

关于结论四的证明和扩展：

①.如果$s[1$～$i-next[i]]$不能作为$s[1$～$i]$循环元，那么

$s[1$～$i-next[?]]$也都一定不能作为$s[1$～$i]$的循环元。

(即结论四)

②.如果$i-next[i]$不可整除$i$，$s[1$～$i]$一定不存在循环元。

③.如果$i-next[i]$不可整除$i$，$i-next[?]$也都一定不可整除$i$。

④.如果$s[1$～$m]$是$s[1$～$i]$的循环元，$next[i]$一定为$i-m$($i-m$一定为

$next[i]$)。(在算法竞赛进阶指南上有这么一句话：如果$s[1$～$m]$为$s[1$～$i]$的循

环元，$i-m$一定是$next[i]$的“候选项”，与此处意义略有不同)

⑤.若$m=i-next[i]$，$j=next[?]$，$next[j]=j-m$。(无论$m$可否整除$i$)

(由④扩展而来)

一些题外话：

关于③的证明，有一个很有趣的想法。

有两个数$a$,$c$和一个数的集合$b$，且$b$与$a$有一定的关系(限制)。

已知$a$不可整除$c$，证明$x(x∈b$)不可整除$c$(目前尚未成功)。

虽然表面上看起来并没有什么用，但这种思想把图形匹配转

化为了代数证明。

如果有大佬感兴趣可以思考一下。。。

附：来自某李姓Math大佬。

②③④比较好理解，这个⑤是个什么意思呢？

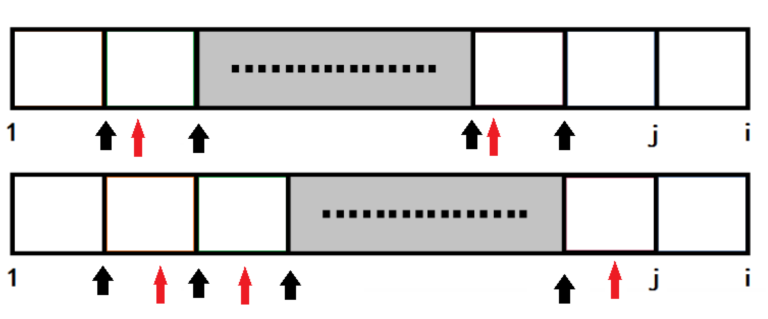
其实不难懂，通俗点说就是$i-next[?]$一定是在$m$的倍数处

$(m,2m,3m...)$，如果有循环，也可以说是$i-next[?]$一定在循环

节点上,或者说是一定在我们先前图片中框选的黑色块的边界相

邻处，不可能在某个黑色块的中间（如图红色为不可能的情况）

注意一下这个等式：$i-next[j]=i-j+m$

可以化简为：$next[j]=j-m$

那么可以发现每个$next[?]$和$next[next[?]]$之间刚好相差m，

只是要由⑤推导①的话，用化简前的样子似乎会更好懂一些。

假如④⑤得证，那么它们和①有什么关系呢？

如果$i-next[?]$一定是在$m$的倍数处$(m=i-next[i])$，

因为当$m$不可整除$i$时，$m$的倍数也不可整除$i$，

所以$i-next[?]$均不满足作为$s[1$～$i]$循环元的条件(前面已

提到过“条件”具体指什么)。

因此，⑤$→$①得证。

如何证明④或者⑤？

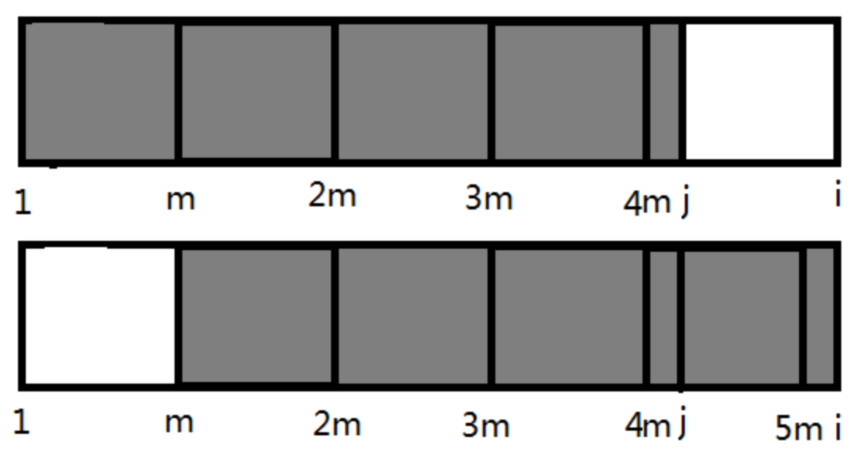
如图，$j=next[i]$，$m=i-next[i]$

先按照与之前相同的方法先将$s[1$～$i]$划分成$K$个黑色块

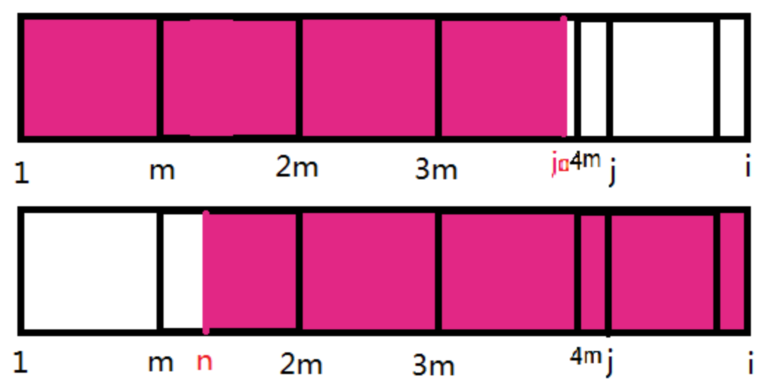
$j0=next[j]$，$n=i-next[j]$，假设n不在m的倍数处，如图红色。

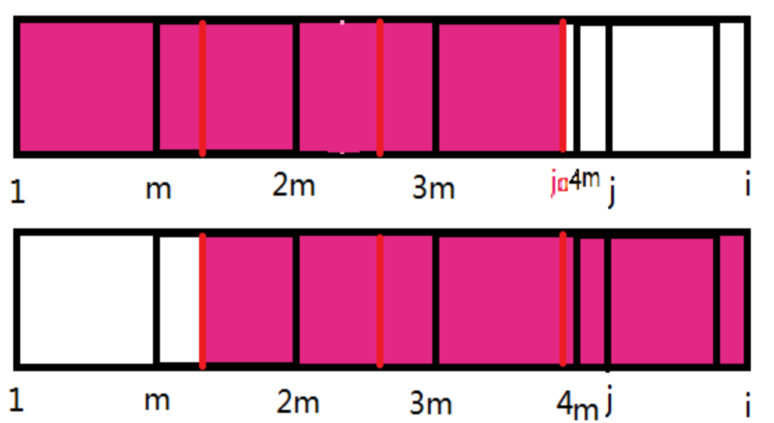
同样的，框选出红色块。

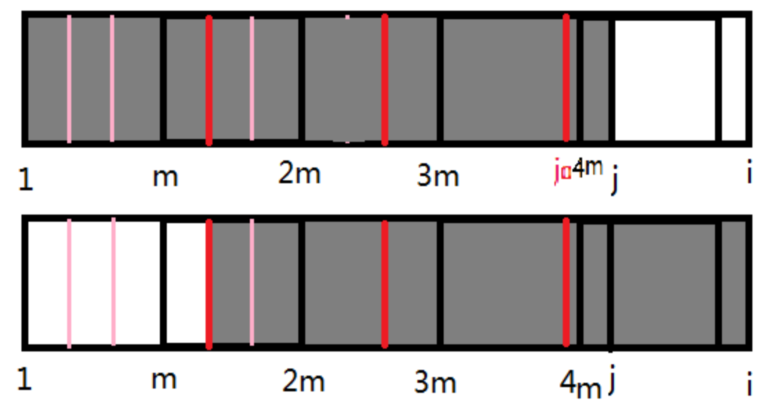
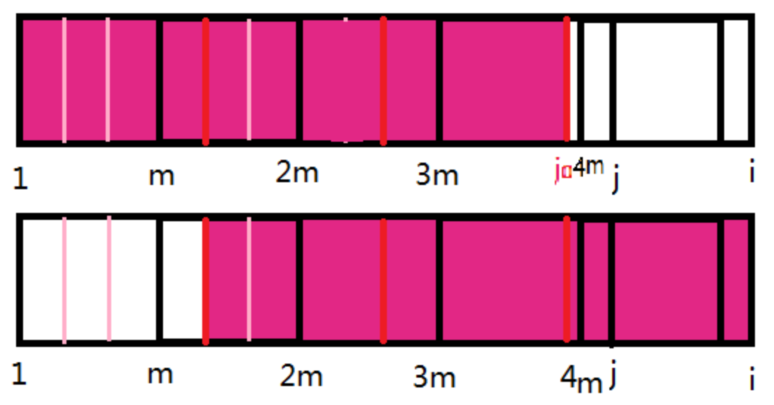
然后再作一些辅助线。接下来就开始推理。

设$v=j-j0$。

先看左边：$s[1$～$1+v]=s[m$～$m+v]$，$s[1+v$～$1+2v]=s[m+v$～$m+2v] $

再看右边： $s[1$～$1+v]=s[m+v$～$m+2v]$

综合可得：$s[1$～$1+v]=s[m$～$m+v]=s[m+v$～$m+2v]=s[1+v$～$1+2v]$

无限的推进，再推进，辅助线划分出的长度为v的区域全部相等，直至边界。而此时的边界出现了两种情况：

⑴v可整除i。

此时刚好将$s[1$～$i]$分成了若干个完全相同的长度为$v$的小块，明显形成了循环元$s[1$～$v]$，那么$next[i]$至少应为$i-v$，这与之前的$next[i]=j$相矛盾。

⑵v不可整除i。

观察下列图片，你发现了什么？

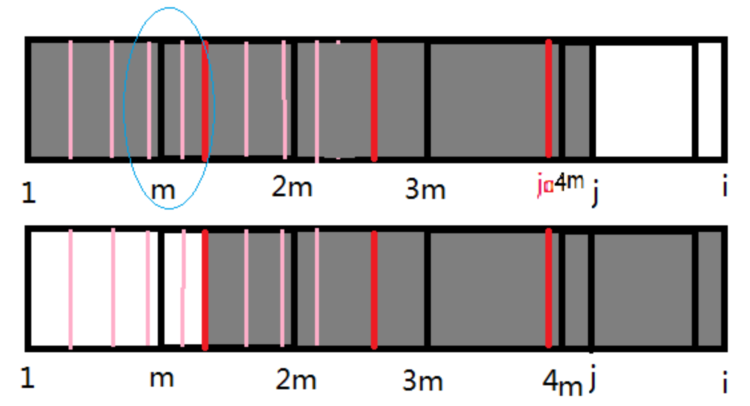
将蓝圈处放大，发现了一种交叉相等的情况(如图绿色处)。

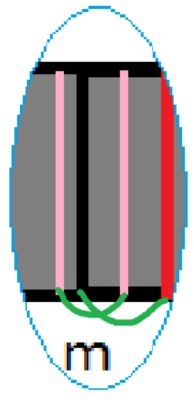
再把它压扁，并取几个新的名字$1',m',j',i'$。此时它变得和初始

的情况一模一样，于是经过相同的操作后，再一次使出了无限

推进，假如每次的$v'$都不可整除$m'$，那么就一路推了边界：$v'=1$。

$1$可以整除任何数，于是$s[1$～$i]$形成了长度为$1$的循环元，矛盾。

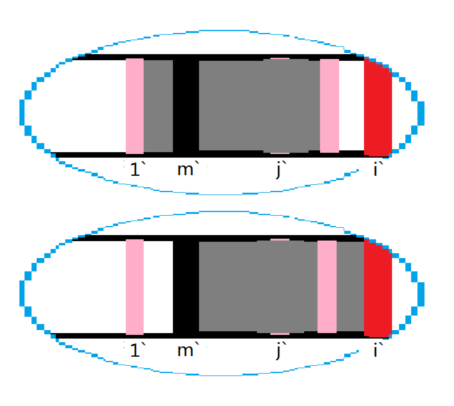
当n不在m的倍数处时，一定会出现矛盾，所以假设不成立。

因此④得证。同理⑤也得证。

完结附代码：

#include<cstdio>

int t,i,j,n,nex[1000005];char a[1000005];

int main(){

    while(scanf("%d",&n),n){

        scanf("%s",a+1);

        printf("Test case #%d\n",++t);

        for(i=2,j=0;i<=n;i++){//最基本的 next[] 数组求法

            while(j&&a[i]!=a[j+1])j=nex[j];

            if(a[i]==a[j+1])j++;nex[i]=j;

        }

        for(i=2;i<=n;i++)//由于1～1只有一个字母，只能是它本身构成长度为1的循环，所以从2开始枚举

            if(i%(i-nex[i])==0&&nex[i])//判断时还要注意nex[i]是否为0

                printf("%d %d\n",i,i/(i-nex[i]));

//如果i含有长度大于1的最小循环元，输出i的长度(即i)以及最大循环次数K(即i-nex[i])

        printf("\n");//记得输出一个空行

    }

}

写了这么多证明，结果最后代码简单得不要不要的。。。。。