[LeetCode] 119. Pascal's Triangle II 杨辉三角之二
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.
Note that the row index starts from 0.

In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 3
Output: [1,3,3,1]
Follow up:
Could you optimize your algorithm to use only O(k) extra space?
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第 n+1 行,此处n为包含0在内的自然数)正好对应于二项式 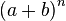 展开的系数。例如第二层 1 2 1 是幂指数为2的二项式
展开的系数。例如第二层 1 2 1 是幂指数为2的二项式 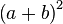 展开形式
展开形式 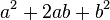 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数 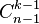 。
。 - 第
 行数字和为
行数字和为 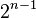 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第  行的第
行的第  个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用 O(k) 的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法, 我最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码请参见评论区一楼。本地调试输出前十行,没啥问题,拿到 OJ 上测试,程序在第 18 行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整型数 int 的数值范围只有 -32768 到 32768 之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的 OJ 肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个 for 循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字,具体实现代码如下:
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> res(rowIndex + );
res[] = ;
for (int i = ; i <= rowIndex; ++i) {
for (int j = i; j >= ; --j) {
res[j] += res[j - ];
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/119
类似题目:
参考资料:
https://leetcode.com/problems/pascals-triangle-ii/
https://leetcode.com/problems/pascals-triangle-ii/discuss/38420/Here-is-my-brief-O(k)-solution
LeetCode All in One 题目讲解汇总(持续更新中...)
[LeetCode] 119. Pascal's Triangle II 杨辉三角之二的更多相关文章
- [LeetCode] 119. Pascal's Triangle II 杨辉三角 II
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- [LeetCode] Pascal's Triangle II 杨辉三角之二
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- Leetcode#118. Pascal's Triangle(杨辉三角)
题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 5 输出: [ [1], [1,1], [1,2, ...
- LeetCode 118. Pascal's Triangle (杨辉三角)
Given numRows, generate the first numRows of Pascal's triangle. For example, given numRows = 5,Retur ...
- LeetCode 119 Pascal's Triangle II
Problem: Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Ret ...
- Leetcode 119 Pascal's Triangle II 数论递推
杨辉三角,这次要输出第rowIndex行 用滚动数组t进行递推 t[(i+1)%2][j] = t[i%2][j] + t[i%2][j - 1]; class Solution { public: ...
- LeetCode 119. Pascal's Triangle II (杨辉三角之二)
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- leetcode 119 Pascal's Triangle II ----- java
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- Java [Leetcode 119]Pascal's Triangle II
题目描述: Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return ...
随机推荐
- torch_10_stackGAN-V2
核心要点 StackGAN旨在生成高分辨率的真实图片. stackGAN-v1架构包含两个阶段:用于文本到图像的合成,阶段1GAN根据给定的文本描述绘制对象的形状和颜色,生成低分辨率图像.阶段2将阶段 ...
- fastadmin表单提交后却没有关闭弹窗
点击操作按钮弹出窗口,操作完之后提交表单,无论操作成功还是失败,窗口都不关闭,操作之后出现一个笑脸,3秒后回到弹框刚打开的样子 而我们想要的是这个效果: 在jS那里给这个按钮绑定一个事件即可实现
- influxdb安装和学习
安装 https://docs.docker.com/samples/library/influxdb/ 先启动,创建admin用户 docker run -d --name influxdb -p ...
- 生成 Visual Studio 中的代码的文档生成神器
当我们在团队开发中的时候,经常要给别人提供文档,有了这个工具,设置一下,一键生成.前提是你要写好xml注释. 这也是开源项目: https://sandcastle.codeplex.com/ 它就是 ...
- 如何判断服务器之间的服务是否可用?ping 还是 telnet?
1. 背景 机器A需要调用机器B的服务,为此要保证服务的可用性,我们有时候用ping,有时候用telent来验证机器A和B的连通性,但有时候会出现这种情况,A可以ping通B,但A调用B的服务会一直报 ...
- ASP.NET Core系列:日志
1. NLog 添加安装包: Install-Package NLog.Web.AspNetCore <?xml version="1.0" encoding="u ...
- CSS 选择器大全
在CSS中,选择器是用于选择要设置样式的元素的模式. 选择器 例子 描述 .class .intro 选择class=“intro”的所有元素 #id #firstname 选择id=“firstna ...
- 基于记忆性的中值滤波O(r)与O(1)复杂度的算法实现
本文参考博客:https://www.cnblogs.com/Imageshop/archive/2013/04/26/3045672.html 原生的中值滤波是基于排序算法的,这样的算法复杂度基本在 ...
- Python元组与字符串操作(8)——三数排序多种实现
练习 依次接收用户输入的3个数,排序后打印 1.转换int后,判断大小排序,使用分支结构完成 num1 = [] for i in range(3): num1.append(int(input('& ...
- Setting up the data and the model
Table of Contents: Setting up the data and the model Data Preprocessing Weight Initialization Batch ...
