JLOI 2009 二叉树问题

洛谷 P3884 [JLOI2009]二叉树问题

洛谷传送门

JDOJ 2024: [JLOI2009]二叉树问题

JDOJ传送门

Description

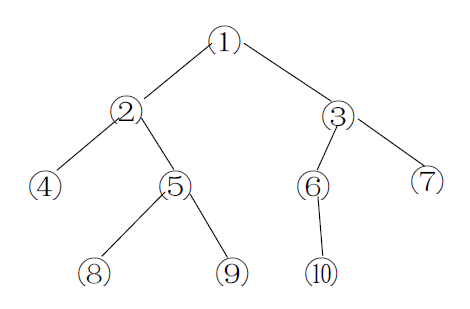
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 　(3×2+2=8)

​ ⑥→⑦为3　 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

Input

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

Output

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

Sample Input

10 1 2 1 3 2 4 2 5 3 6 3 7 5 8 5 9 6 10 8 6

Sample Output

4 4 8

一道LCA的好题。

介绍一下大体思路和自己出的bug。

首先存边，存边的时候要存单向边，要不然深搜的时候会卡死在里面。

然后是深搜，深搜主要是预处理的过程，预处理deep数组和fa数组分别记录每个点的深度和父亲节点。具体实现见代码。

然后我们开始枚举最大深度和最大宽度，详见代码，截至此时就出了前两个答案。

最后就是LCA的过程。

可以写倍增LCA，但是倍增LCA其实就是普通朴素LCA的优化，所以我写了朴素LCA（就会这个）（俗名爬一爬）。

这里的LCA函数不是记录公共祖先，而是记录这两个点各向上爬了多少的深度，这里要注意！！因为你会有swap操作，所以你swap之后你的depth1和depth2记录的点向上爬的距离要反着取（以前是1记录x,2记录y，现在要反过来）

然后就可以AC了。

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n,ans1,ans2,depth1,depth2;
int tot,to[202],nxt[202],head[101];
int fa[101],deep[101],width[101];
void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int pre,int step)
{
	fa[x]=pre;
	deep[x]=step;
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		dfs(y,x,step+1);
	}
}
void lca(int x,int y)
{
	if(deep[x]<deep[y])
	{
		swap(x,y);
		while(deep[x]>deep[y])
			x=fa[x],depth2++;
		while(x!=y)
		{
			x=fa[x],y=fa[y];
			depth2++;
			depth1++;
		}
	}
	else
	{
		while(deep[x]>deep[y])
			x=fa[x],depth1++;
		while(x!=y)
		{
			x=fa[x],y=fa[y];
			depth1++;
			depth2++;
		}
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n-1;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	dfs(1,0,1);
	for(int i=1;i<=n;i++)
		width[deep[i]]++;
	for(int i=1;i<=n;i++)
		ans1=max(ans1,deep[i]);
	for(int i=1;i<=n;i++)
		ans2=max(ans2,width[i]);
	int u,v;
	scanf("%d%d",&u,&v);
	lca(u,v);
	printf("%d\n%d\n%d",ans1,ans2,depth1*2+depth2);
	return 0;
}