Codeforces Round #405 (rated, Div. 2, based on VK Cup 2017 Round 1) D

Description

A tree is an undirected connected graph without cycles. The distance between two vertices is the number of edges in a simple path between them.

Limak is a little polar bear. He lives in a tree that consists of n vertices, numbered 1 through n.

Limak recently learned how to jump. He can jump from a vertex to any vertex within distance at most k.

For a pair of vertices (s, t) we define f(s, t) as the minimum number of jumps Limak needs to get from s to t. Your task is to find the sum off(s, t) over all pairs of vertices (s, t) such that s < t.

Input

The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ 5) — the number of vertices in the tree and the maximum allowed jump distance respectively.

The next n - 1 lines describe edges in the tree. The i-th of those lines contains two integers a_i and b_i (1 ≤ a_i, b_i≤ n) — the indices on vertices connected with i-th edge.

It's guaranteed that the given edges form a tree.

Output

Print one integer, denoting the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.

Examples

input

6 2
1 2
1 3
2 4
2 5
4 6

output

20

input

13 3
1 2
3 2
4 2
5 2
3 6
10 6
6 7
6 13
5 8
5 9
9 11
11 12

output

114

input

3 5
2 1
3 1

output

3

Note

In the first sample, the given tree has 6 vertices and it's displayed on the drawing below. Limak can jump to any vertex within distance at most2. For example, from the vertex 5 he can jump to any of vertices: 1, 2 and 4 (well, he can also jump to the vertex 5 itself).

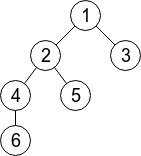
There are 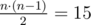 pairs of vertices (s, t) such that s < t. For 5 of those pairs Limak would need two jumps:(1, 6), (3, 4), (3, 5), (3, 6), (5, 6). For other 10 pairs one jump is enough. So, the answer is 5·2 + 10·1 = 20.

In the third sample, Limak can jump between every two vertices directly. There are 3 pairs of vertices (s < t), so the answer is 3·1 = 3.

题意：给出一棵树，和最多跳K个数字，f(s,t)表示从s到t需要跳的最少次数，问那么一棵树每两个点跳的次数之和是多少？

解法：如果只跳一次，那每个点经历的次数为这个点的子树节点个数*（n-这个点的子树节点个数），那么K>=2的情况，对于任意两个点的x->y 距离为 深度[x]+深度[y]-2*最近公共祖先深度[z]

dp[v][d%k]表示v为节点开始，深度为d%k的个数，比如2为节点开始,深度为1的有4和5

4在2的子树内，4开始深度为1点为6，我们更新到dp[2][1]内，就是dp[2][1]+=dp[4][1]

sum[v]表示v的子树节点个数

最后答案为ans/n，比如距离为5，最多跳3步，其实是跳（5+1）/3=2次就好了，注释也有解释

(题解好难懂啊，我也不知道说清楚了没)

 #include<bits/stdc++.h>
 using namespace std;
 #define  ll long long
 const int maxn=;
 ll dp[maxn][],sum[maxn];
 vector<int>q[maxn];
 ll vis[maxn];
 ll cnt;
 ll n,k;
 void dfs(int v,int d,int fa)
 {
     dp[v][d%k]=sum[v]=;
     //当前子节点就v一个
     for(int i=;i<q[v].size();i++)
     {
        // cout<<v<<endl;
         int pos=q[v][i];
         if(pos==fa) continue;
         dfs(pos,d+,v);
         for(int x=;x<k;x++)
         {
             for(int y=;y<k;y++)
             {
                 int ans=((x+y)%k-(d*)%k+k)%k;
                 //ans为缺少部分，比如5跳3,少了两步
                 cnt+=((k-ans)%k)*dp[v][x]*dp[pos][y];
                 //少了两步，为了达成三步,必须多走一步，所以为k-ans,每个点多走k-ans步，相乘
             }
         }
         for(int x=;x<k;x++)
         {
             dp[v][x]+=dp[pos][x];
             //子节点记录部分更新到父结点
         }
         cnt+=sum[pos]*(n-sum[pos]);
         //讨论k=1的情况，种数==为pos节点包含子节点*以外的节点
         sum[v]+=sum[pos];
         //将pos包含节点个数更新到父结点

     }
 }
 int main()
 {
     cin>>n>>k;
     for(int i=;i<n-;i++)
     {
         int u,v;
         cin>>u>>v;
         q[u].push_back(v);
         q[v].push_back(u);
     }
     dfs(,,);
     cout<<cnt/k<<endl;
     return ;
 }