数据结构实验7：实现二分查找、二叉排序（查找）树和AVL树

实验7

学号：      姓名：     专业：

7.1实验目的

(1) 掌握顺序表的查找方法，尤其是二分查找方法。

(2) 掌握二叉排序树的建立及查找。

查找是软件设计中的最常用的运算，查找所涉及到的表结构的不同决定了查找的方法及其性能。二分查找是顺序表的查找中的最重要的方法，应能充分理解其实现方法和有关性能，并能借助其判定树结构来加深理解。二叉排序树结构在实验时具有一定的难度，可结合二叉树的有关内容和方法来实现。

7.2 实验任务

编写算法实现下列问题的求解。

(1) 对下列数据表，分别采用二分查找算法实现查找，给出查找过程依次所比较的元素（的下标），并以二分查找的判定树来解释。

第一组测试数据：

数据表为 (1,2,3,4,6,7,8,9,10,11,12,13,17,18,19,20,24,25,26,30,35,40,45,50,100)

查找的元素分别为： 2，8，20,  30，50，5，15，33，110

第二组数据：

数据表为 (2,3,5,7,8,10,12,15,18,20,22,25,30,35,40,45,50,55,60, 80,100)

查找的元素分别为： 22，8，80，3，100，1，13，120

(2) 设计出在二叉排序树中插入结点的算法，在此基础上实现构建二叉排序树的算法。

测试数据：构建二叉排序树的输入序列如下：

第一组数据：

100，150，120，50，70，60，80，170，180，160，110，30，40，35，175

第二组数据：

100，70，60，80，150，120，50，160，30，40，170，180，175，35

(3) 设计算法在二叉排序树中查找指定值的结点。

测试数据：在任务<1>中第一组测试数据所构造的二叉排序树中，分别查找下列元素：    150，70，160，190，10，55，175

(4) 设计算法在二叉排序树中删除特定值的结点。

测试数据：在任务(1)中第一组测试数据所构造的二叉排序树中，分别删除下列元素：30，150，100

(5) 已知整型数组A[1..26]递增有序，设计算法以构造一棵平衡的二叉排序树来存放该数组中的所有元素。

测试数据：数组元素分别为：

第一组数据：

（1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26）

第二组数据：

（1,3,6,10,15,21,28,36,45,55,66,78,91,105,120,136,153,171,190,210,231,253,277,302,328）

7.3实验数据要求

自我编写测试样例，要求每个功能函数的测试样例不少于两组

7.4 运行结果截图及说明

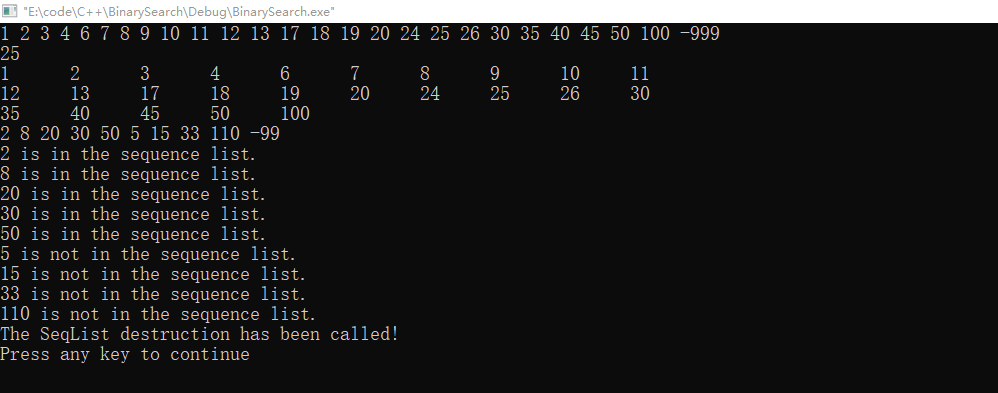
图1 测试（1）①

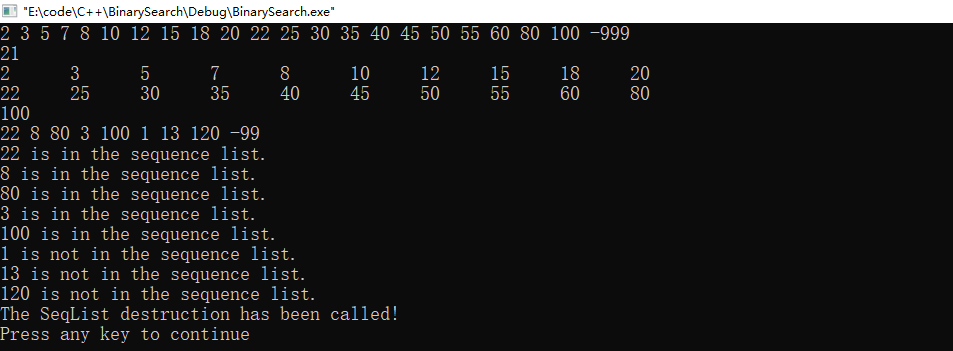
图2 测试（1）②

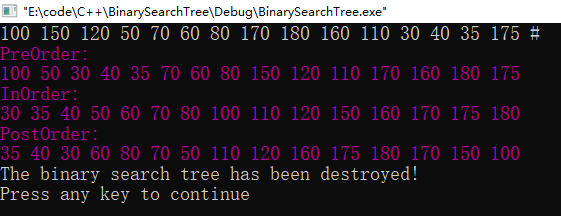
图3 测试（2）①

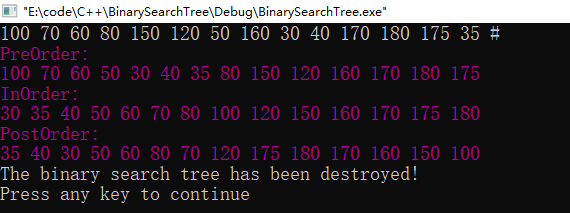
图4 测试（2）②

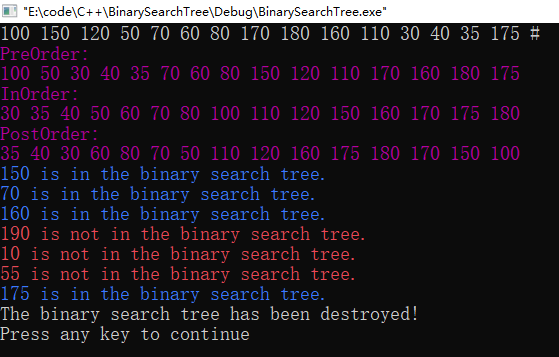
图5 测试（3）

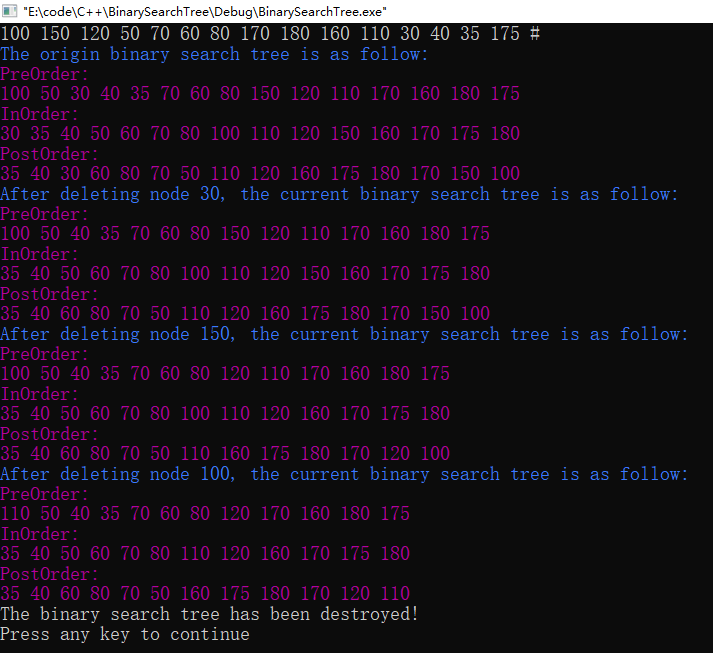
图6 测试（4）

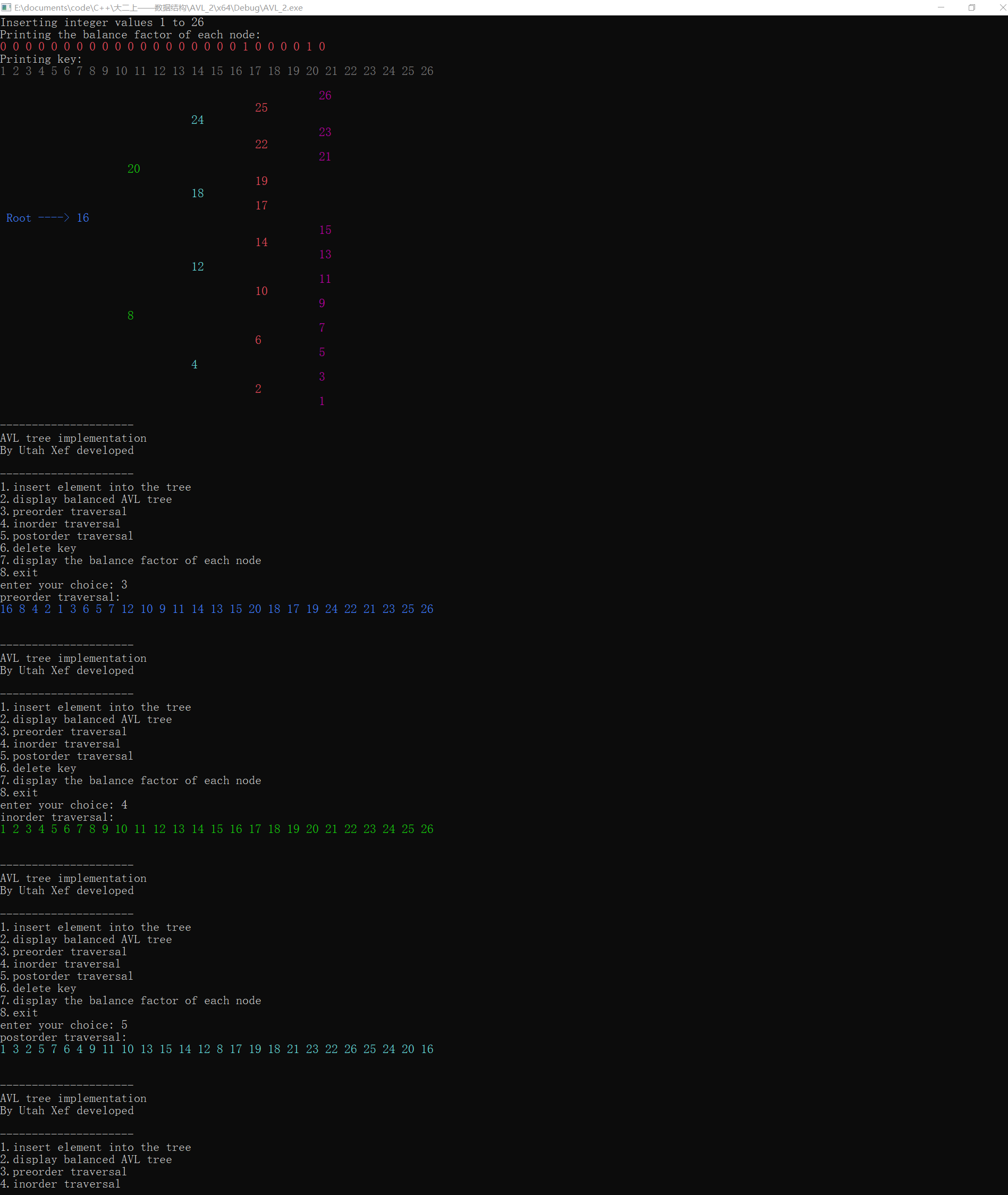
图7 测试（5）①

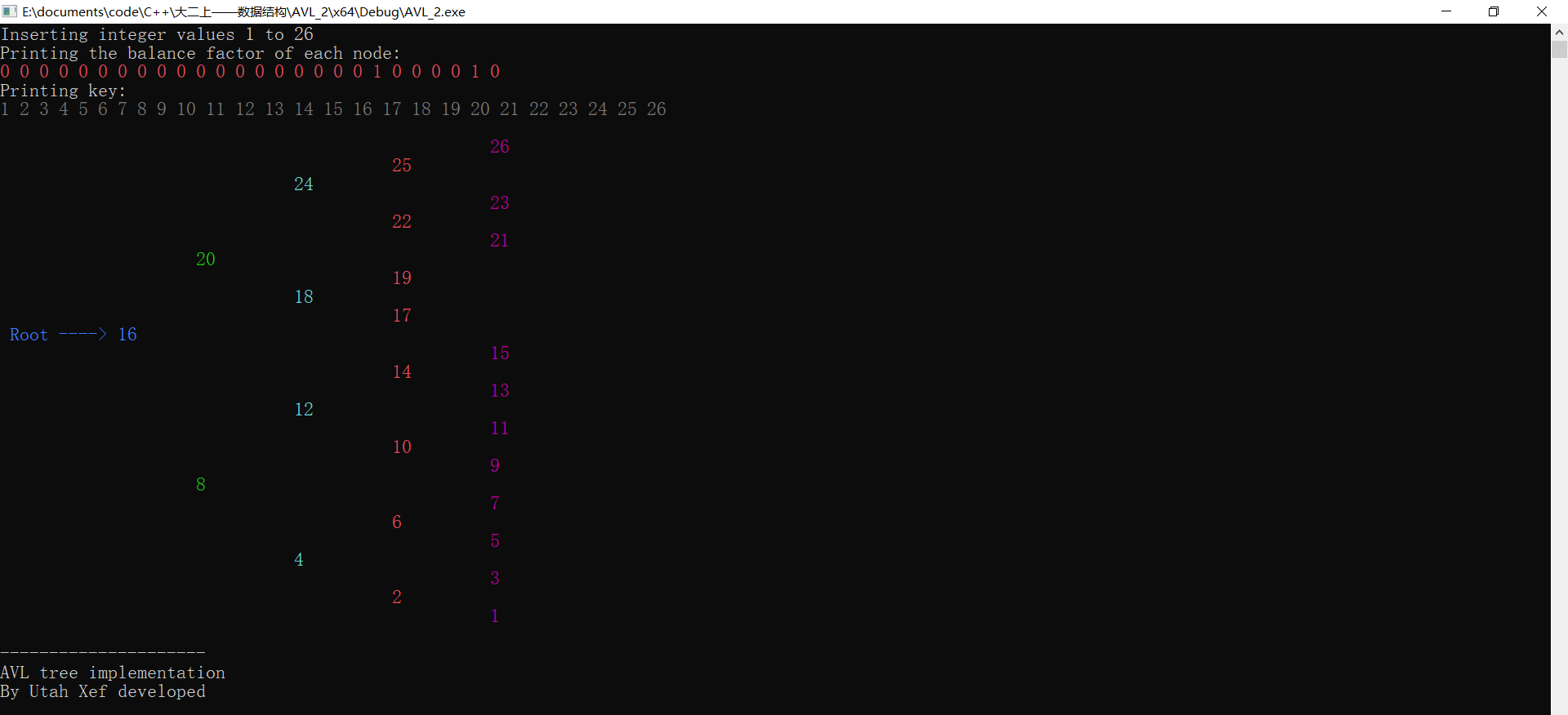
图8 测试（5）①

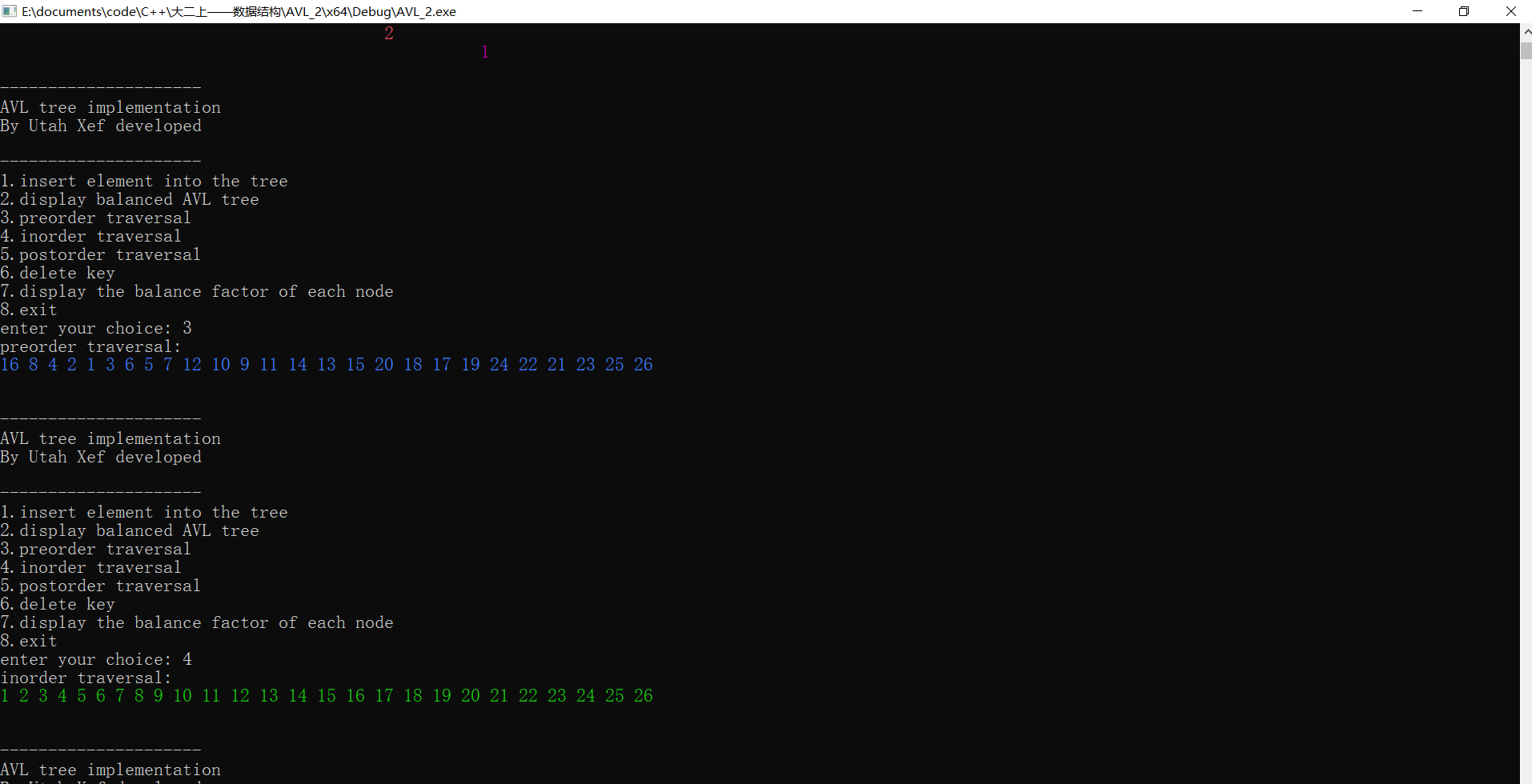
图9 测试（5）①

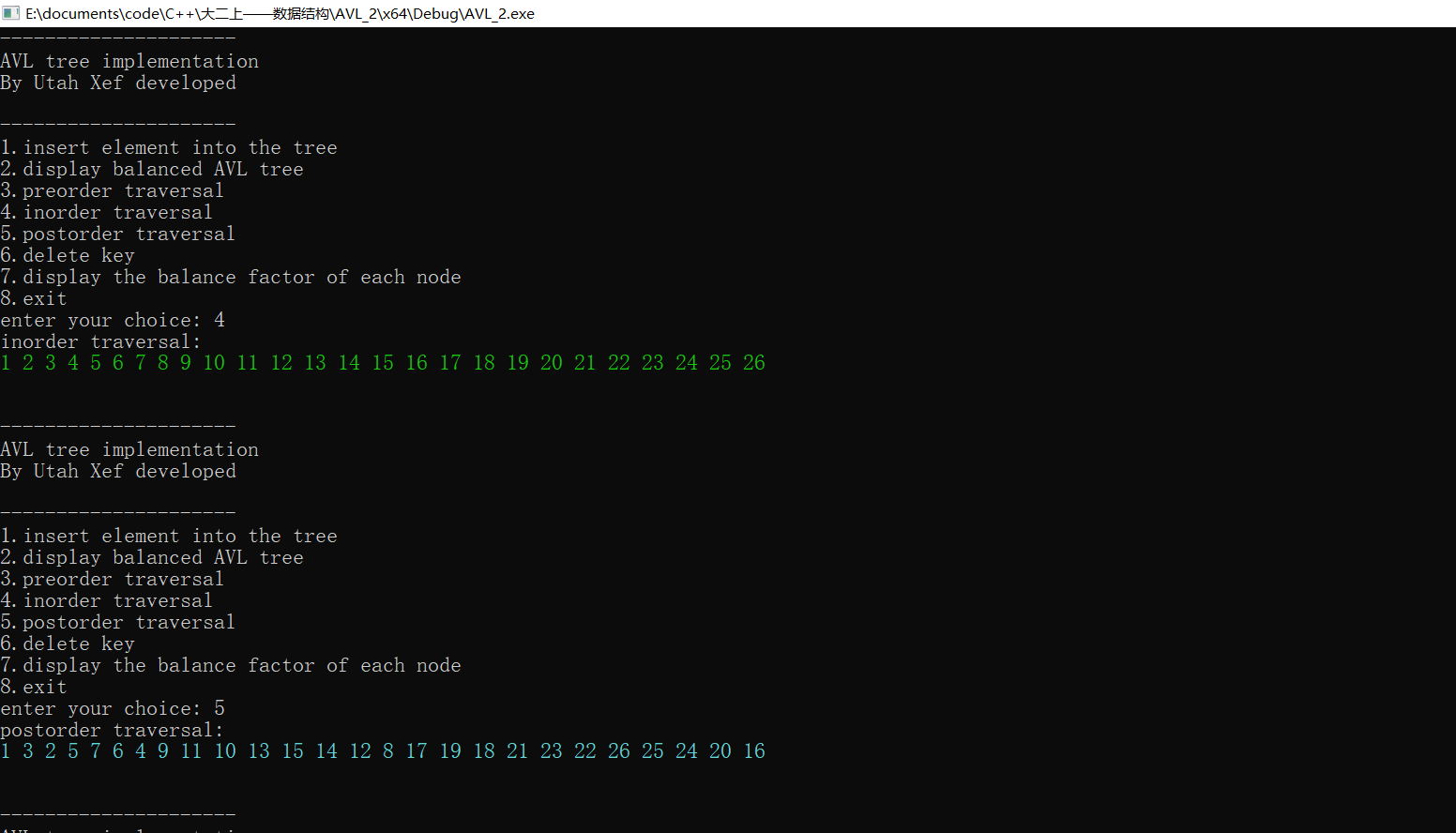
图10 测试（5）①

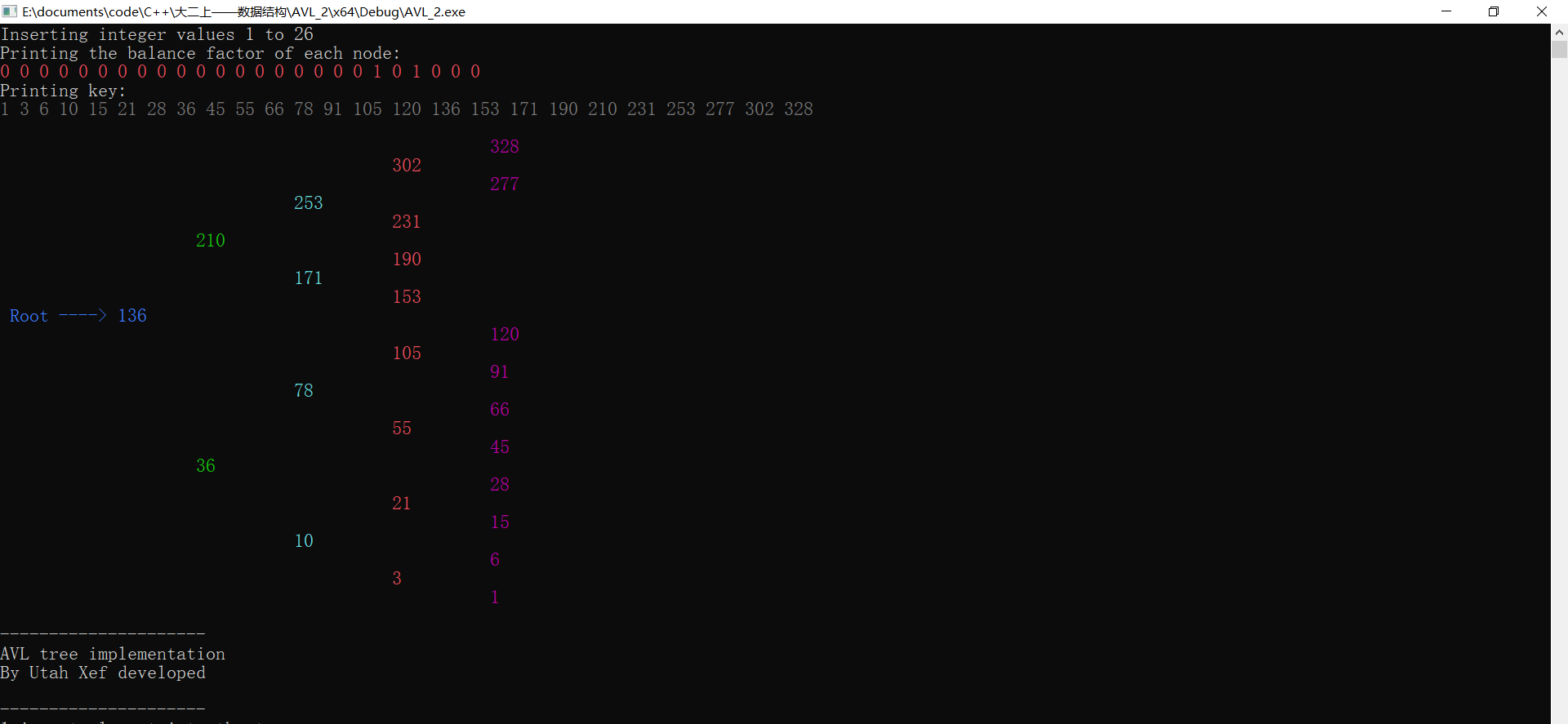
图11 测试（5）②

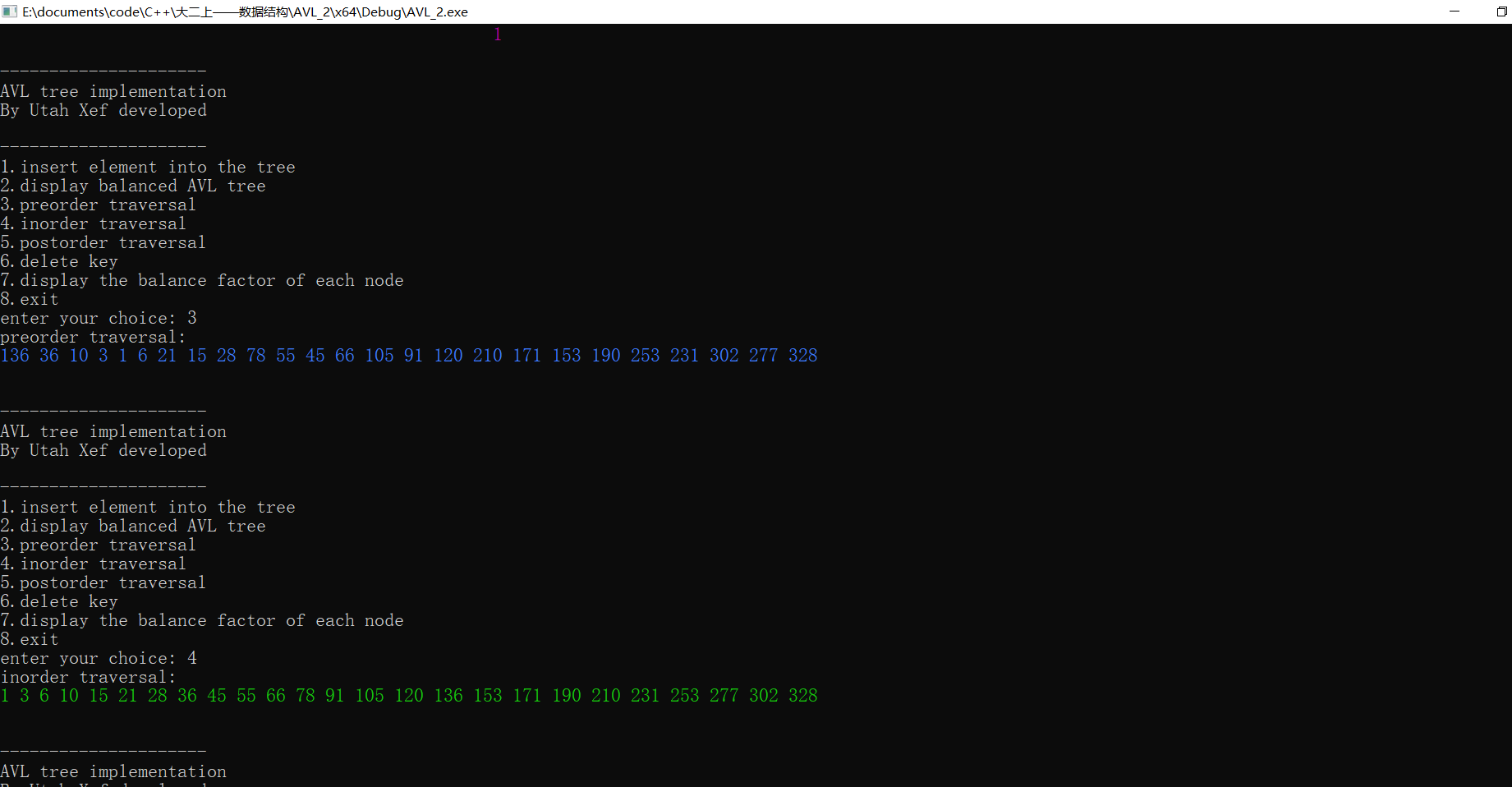
图12 测试（5）②

图13 测试（5）②

图14 测试（5）①（全）

图15 测试（5）②（全）

7.5 附源代码

二分查找：

 // stdafx.h : include file for standard system include files,
 //  or project specific include files that are used frequently, but
 //      are changed infrequently
 //

 #if !defined(AFX_STDAFX_H__940FF418_5647_412A_8B4F_3C89C07F8CA5__INCLUDED_)
 #define AFX_STDAFX_H__940FF418_5647_412A_8B4F_3C89C07F8CA5__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 #include <stdc++.h>

 using namespace std;

 typedef long elementType;

 const long maxn =  + ; 

 // TODO: reference additional headers your program requires here

 //{{AFX_INSERT_LOCATION}}
 // Microsoft Visual C++ will insert additional declarations immediately before the previous line.

 #endif // !defined(AFX_STDAFX_H__940FF418_5647_412A_8B4F_3C89C07F8CA5__INCLUDED_)

 // SeqList.h: interface for the SeqList class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX_SEQLIST_H__58D90762_85EC_4BBB_94EA_068A582CCD81__INCLUDED_)
 #define AFX_SEQLIST_H__58D90762_85EC_4BBB_94EA_068A582CCD81__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 class SeqList
 {
 public:
     SeqList();
     virtual ~SeqList();
     bool seqListFull();
     bool seqListEmpty();
     void randomInsert( elementType number );
     void insert( elementType value );
     void showLength();
     elementType binarySearch( elementType value );
     friend ostream &operator<<( ostream &os, SeqList &SL )
     {
         if( SL.length == - )
         {
             return os;
         }
         int column = ;
         for( int i = ; i <= SL.length; i ++ )
         {
             os << setw() << setiosflags( ios::left ) << SL.Arr[i] << " ";
             column ++;
             if( column %  ==  )
                 os << endl;
         }
         os << endl;
     }

 private:
     elementType Arr[maxn];
     int length;

 };

 #endif // !defined(AFX_SEQLIST_H__58D90762_85EC_4BBB_94EA_068A582CCD81__INCLUDED_)

 // SeqList.cpp: implementation of the SeqList class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "SeqList.h"

 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 SeqList::SeqList()
 {
     length = ;
 }

 SeqList::~SeqList()
 {
     ios::sync_with_stdio(false);
     cout << "The SeqList destruction has been called!" << endl;
 }

 bool SeqList::seqListFull()
 {
     return length == maxn - ;
 }

 bool SeqList::seqListEmpty()
 {
     return length == ;
 }

 void SeqList::randomInsert( elementType number )
 {
     ios::sync_with_stdio(false);
     if( seqListFull() )
     {
         cerr << "Inserting failed!The sequence list has been full.Error in void SeqList::randomInsert( int number )" << endl;
         return;
     }

     srand( time(NULL) );
     elementType last = -;
     for( int i = ; i < number; i ++ )
     {
         elementType key = rand() % (  -  +  ) + ;
         if( key >= last )
         {
             length ++;
             Arr[length] = key;
             last = key;
         }
         else
         {
             i --;
         }
     }
 }

 void SeqList::insert( elementType value )
 {
     ios::sync_with_stdio(false);
     if( seqListFull() )
     {
         cerr << "Inerting failed!The sequence list has been full.Error in void SeqList::insert( elementType value )" << endl;
         return;
     }

     length ++;
     Arr[length] = value;
 }

 elementType SeqList::binarySearch( elementType value )
 {
     ios::sync_with_stdio(false);
     if( seqListEmpty() )
     {
         cerr << "Searching failed!The sequence list is empty.Error in elementType SeqList::binarySearch( elementType value )" << endl;
         return -;
     }
     elementType lower = , upper = length;
     while( lower <= upper )
     {
         elementType mid = ( lower + upper ) >> ; //+ 1;
         if( Arr[mid] == value )
         {
             return mid;
         }
         if( Arr[mid] >= value )
         {
             upper = mid - ;
         }
         else
         {
             lower = mid + ;
         }
     }
     return -;
 }

 void SeqList::showLength()
 {
     ios::sync_with_stdio(false);
     cout << length << endl;
 }

 // BinarySearch.cpp : Defines the entry point for the console application.
 //

 #include "stdafx.h"
 #include "SeqList.h"

 void test1()
 {
     ios::sync_with_stdio(false);
     SeqList SL1;
     elementType number;
     cin >> number;
     SL1.randomInsert( number );
     cout << SL1;
     elementType value;
     for( int i = ; i < number; i ++ )
     {
         cin >> value;
         if( SL1.binarySearch(value) != - )
         {
             cout << value << " is in the sequence list." << endl;
         }
         else
         {
             cout << value << " is not in the sequence list." << endl;
         }
     }
 }

 void test2()
 {
     ios::sync_with_stdio(false);
     SeqList SL1;
     elementType value;
     while( cin >> value )
     {
         if( value == - )
         {
             break;
         }
         SL1.insert(value);
     }
     SL1.showLength();
     cout << SL1;

     elementType key;
     while( cin >> key )
     {
         //cin >> key;
         if( key == - )
         {
             //break;
             return;
         }
         if( SL1.binarySearch(key) != - )
         {
             cout << key << " is in the sequence list." << endl;
         }
         else
         {
             cout << key << " is not in the sequence list." << endl;
         }
     }

 }

 int main(int argc, char* argv[])
 {
     test2();

     return ;
 }

二分查找（排序）树：

 // stdafx.h : include file for standard system include files,
 //  or project specific include files that are used frequently, but
 //      are changed infrequently
 //

 #if !defined(AFX_STDAFX_H__239FA301_F6C5_4AE4_BD82_5EB3365C7ECB__INCLUDED_)
 #define AFX_STDAFX_H__239FA301_F6C5_4AE4_BD82_5EB3365C7ECB__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 #include <stdc++.h>
 #include <graphics.h>

 using namespace std;

 //将 elementType 设为 int 可以顺利完成实验要求；而将其设为 string 则可以输入字符串等，
 //此时的大小关系默认为为字典序
 //typedef string elementType;
 typedef int elementType;

 //为了图好玩，调用EasyX库把字体颜色改了一下
 //这是EasyX的官方网站： https://www.easyx.cn/

 typedef struct node
 {
     elementType data;
     struct node *leftChidld, *rightChild;
 }BSTNode, *_BSTree;

 // TODO: reference additional headers your program requires here

 //{{AFX_INSERT_LOCATION}}
 // Microsoft Visual C++ will insert additional declarations immediately before the previous line.

 #endif // !defined(AFX_STDAFX_H__239FA301_F6C5_4AE4_BD82_5EB3365C7ECB__INCLUDED_)

 // BSTree.h: interface for the BSTree class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX_BSTREE_H__37E371A7_E165_4AC3_898B_DDF38B0F87D8__INCLUDED_)
 #define AFX_BSTREE_H__37E371A7_E165_4AC3_898B_DDF38B0F87D8__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 class BSTree
 {
 public:
     BSTree();
     virtual ~BSTree();
     BSTNode *search( _BSTree BST, elementType value );//递归查找
     BSTNode *search( _BSTree BST, elementType value, _BSTree &father );//迭代查找
     BSTNode *getRootNode();
     bool insert( _BSTree BST, elementType value );

     bool deleteNode1( _BSTree &BST, elementType value );    //删除指定结点，failed
     void deleteNode2( _BSTree &BST, elementType value );    //递归删除指定结点
     void deleteNode2_1( _BSTree &BST, elementType value );    //迭代删除指定结点，待调试！
     void deleteNode3( _BSTree &BST, elementType value );

     void removeNode1( _BSTree &BST );
     void removeNode2( _BSTree &BST );
     void removeNode3( _BSTree &BST );

     void createBinarySearchTree( _BSTree BST, vector<elementType>VI/*elementType value*/ );
     void destroy( _BSTree BST );
     void preOrderTraversal( _BSTree BST/*, int space*/ );
     void inOrderTraversal( _BSTree BST/*, int space*/ );
     void postOrderTraversal( _BSTree BST/*, int space*/ );
 private:
     BSTNode *head;
 };

 #endif // !defined(AFX_BSTREE_H__37E371A7_E165_4AC3_898B_DDF38B0F87D8__INCLUDED_)

 // BSTree.cpp: implementation of the BSTree class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "BSTree.h"

 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 BSTree::BSTree()
 {
     //head = NULL;
     //head = new BSTNode;
     //head->leftChidld = head->rightChild = NULL;
 }

 BSTree::~BSTree()
 {
     ios::sync_with_stdio(false);
     destroy(head);
     cout << "The binary search tree has been destroyed!" << endl;
 }

 void BSTree::destroy( _BSTree BST )
 {
     if(BST)
     {
         destroy( BST->leftChidld );
         destroy( BST->rightChild );
         delete BST;
     }
 }

 void BSTree::preOrderTraversal( _BSTree BST/*, int space*/ )
 {
     ios::sync_with_stdio(false);
     /*
     if(!BST)
     {
         cerr << "The binary search tree is empty.Error in void BSTree::preOrderTraversal( _BSTree BST )." << endl;
         return;
     }
     */
     if(BST)
     {
         cout << BST->data << " ";
         preOrderTraversal( BST->leftChidld );
         preOrderTraversal( BST->rightChild );

         //for( int i  = 0; i < space; i ++ )
         //    cout << " ";
         //cout << BST->data << endl;
         //preOrderTraversal( BST->leftChidld, space + 5 );
         //preOrderTraversal( BST->rightChild, space + 5 );
     }
 }

 void BSTree::inOrderTraversal( _BSTree BST/*, int space*/ )
 {
     ios::sync_with_stdio(false);
     if(BST)
     {
         inOrderTraversal( BST->leftChidld );
         cout << BST->data << " ";
         inOrderTraversal( BST->rightChild );

         //inOrderTraversal( BST->leftChidld, space + 5 );
         //for( int i  = 0; i < space; i ++ )
         //    cout << " ";
         //cout << BST->data << endl;
         //inOrderTraversal( BST->rightChild, space + 5 );
     }
 }

 void BSTree::postOrderTraversal( _BSTree BST/*, int space*/ )
 {
     ios::sync_with_stdio(false);
     if(BST)
     {
         postOrderTraversal( BST->leftChidld );
         postOrderTraversal( BST->rightChild );
         cout << BST->data << " ";

         /*
         postOrderTraversal( BST->leftChidld, space + 5 );
         postOrderTraversal( BST->rightChild, space + 5 );
         for( int i  = 0; i < space; i ++ )
             cout << " ";
         cout << BST->data << endl;
         */
     }
 }

 void BSTree::createBinarySearchTree( _BSTree BST, /*elementType value*/vector<elementType>VI )
 {
     //BST = NULL;
     head = NULL;
     for( int i = ; i < VI.size(); i ++ )
     {
         insert( head, VI[i] );
     }
     return;
     /*
     while( cin >> value )
     {
         if( value == "#" )
         {
             return;
         }
         else
             insert( head, value );
     }

     for( int i = 0; i < value; i ++ )
     {
         elementType key;
         cout << "input: ";
         cin >> key;
         insert( head, key );
     }
     */
 }

 BSTNode *BSTree::getRootNode()
 {
     return head;
 }

 BSTNode *BSTree::search( _BSTree BST, elementType value )//递归查找
 {
     ios::sync_with_stdio(false);
     if(!head)
     {
         cerr << "The binary search tree is empty.Error in BSTNode *BSTree::search( _BSTree BST, elementType value )." << endl;
         return NULL;
     }
     else if( BST->data == value )
     {
         return BST;
     }
     else if( BST->data > value )
     {
         return search( BST->leftChidld, value );
     }
     else
     {
         return search( BST->rightChild, value );
     }
 }

 BSTNode *BSTree::search( _BSTree BST, elementType value, _BSTree &father )//迭代查找
 {
     ios::sync_with_stdio(false);
     /*
     if(!head)
     {
         cerr << "The binary search tree empty.Error in BSTNode *BSTree::search( _BSTree BST, elementType value, _BSTree &father )." << endl;
         return NULL;
     }
     */
     BSTNode *tmp = head;
     father = NULL;
     while( tmp && tmp->data != value )
     {
         father = tmp;
         if( value < tmp->data )
         {
             tmp = tmp->leftChidld;
         }
         else
         {
             tmp = tmp->rightChild;
         }
     }
     return tmp;
 }

 bool BSTree::insert( _BSTree BST, elementType value )
 {
     //if(!head)
     //{
     //    cerr << "The binary search tree does not exit.Error in bool BSTree::insert( _BSTree BST, elementType value )" << endl;
     //    return false;
     //}
     BSTNode *newNode, *target, *father;

     target = search( head, value, father );
     if(target)
     {
         cerr << "Inserting failed!" << value << " has been exited in the binary search tree.\nError in bool BSTree::insert( _BSTree BST, elementType value )" << endl;
         return false;
     }
     newNode = new BSTNode;
     newNode->data =  value;
     newNode->leftChidld = newNode->rightChild = NULL;
     if(!head)
     {
         head = newNode;
     }
     else if( value < father->data )
     {
         father->leftChidld = newNode;
     }
     else
     {
         father->rightChild = newNode;
     }
     return true;
 }

 bool BSTree::deleteNode1( _BSTree &BST, elementType value )
 {
     ios::sync_with_stdio(false);
     //if(!head)
     if(!BST)
     {
         cerr << "The binary search tree does not exit.Error in bool BSTree::deleteNode( _BSTree BST, elementType value )" << endl;
         return false;
     }
     BSTNode *newNode, *target, *father;
     //target = search( head, value, father );
     target = search( BST, value, father );
     if( !target )//查找失败，不删除
     {
         cerr << "Node-deleting failed!\n" << value << " is not in the binary search tree.\n" << "Error in bool BSTree::deleteNode( _BSTree BST, elementType value )." << endl;
         return false;
     }
     if( target->leftChidld && target->rightChild )//被删结点有两个 *target 孩子节点
     {
         newNode = target->rightChild;            //找 target 的中序后继 newNode
         father = target;
         while( newNode->leftChidld )
         {
             father = newNode;
             newNode = newNode->leftChidld;
         }
         target->data = newNode->data;        //将 *newNode 的数据传給 *target
         target = newNode;                    //找到的这个结点成为被删除结点
     }
     if( target->leftChidld )            //单孩子，记录非空孩子结点
     {
         newNode = target->leftChidld;
     }
     else
     {
         newNode = target->rightChild;
     }
     //if( target == head )                    //被删结点是根结点
     if( target == BST )
     {
         //head = newNode;
         BST = newNode;
     }
     else if( newNode && ( newNode->data < father->data ) )        //重新链接，保持二叉排序树
     {
         father->leftChidld = newNode;
     }
     else
     {
         father->rightChild = newNode;
     }
     delete target;
     return true;
 }

 void BSTree::deleteNode2( _BSTree &BST, elementType value )
 {
     if(BST)
     {
         if( value < BST->data )
         {
             deleteNode2( BST->leftChidld, value );
         }
         else if( value > BST->data )
         {
             deleteNode2( BST->rightChild, value );
         }
         else
         {
             removeNode1(BST);
         }
     }
 }

 void BSTree::deleteNode2_1( _BSTree &BST, elementType value )    //迭代删除指定结点，待调试！
 {
     BSTNode *target = NULL;
     while( BST || BST->data != value )
     {
         target = BST;
         if( value < target->data )
         //if( value < BST->data )
             BST = BST->leftChidld;
         else
             BST = BST->rightChild;
     }
     removeNode1(target);
     //removeNode1(BST);
 }

 void BSTree::deleteNode3( _BSTree &BST, elementType value )
 {
     if(BST)
     {
         if( value < BST->data )
         {
             deleteNode2( BST->leftChidld, value );
         }
         else if( value > BST->data )
         {
             deleteNode2( BST->rightChild, value );
         }
         else
         {
             removeNode2(BST);
         }
     }
 }
 /*
 在二叉查找树中删除一个给定的结点p有三种情况

 (1)结点p无左右子树，则直接删除该结点，修改父节点相应指针

 (2)结点p有左子树（右子树），则把p的左子树（右子树）接到p的父节点上

 (3)左右子树同时存在，则有三种处理方式

     a.找到结点p的中序直接前驱结点s，把结点s的数据转移到结点p，然后删除结点s，
     由于结点s为p的左子树中最右的结点，因而s无右子树，删除结点s可以归结到情况(2)。
     严蔚敏数据结构P230-231就是该处理方式。
     b.找到结点p的中序直接后继结点s，把结点s的数据转移到结点p，然后删除结点s，
     由于结点s为p的右子树总最左的结点，因而s无左子树，删除结点s可以归结到情况(2)。
     算法导论第2版P156-157该是该处理方式。
     c.到p的中序直接前驱s，将p的左子树接到父节点上，将p的右子树接到s的右子树上，然后删除结点p。
 */
 void BSTree::removeNode1( _BSTree &BST )
 {
     BSTNode *target = NULL;
     if( !BST->leftChidld )
     {
         target = BST;
         BST = BST->rightChild;
         delete target;
     }
     else if( !BST->rightChild )
     {
         target = BST;
         BST = BST->leftChidld;
         delete target;
     }
     else
     {
         BSTNode *newNode = NULL;
         target = BST;
         newNode = BST->leftChidld;        //左子树根结点
         while( newNode->rightChild )    //寻找 BST 结点的中序前驱结点，即以 BST->leftChild为根结点的子树中的最右结点
         {
             target = newNode;            //*target 指向 *BST 的父结点
             newNode = newNode->rightChild;            //*newNode 指向 *BST 的中序前驱结点
         }
         BST->data = newNode->data;        //*newNode 的数据传給 *BST 的数据，然后删除结点 *newNode
         if( target != BST )                //BST->leftChidld 的右子树非空，这句话等价于 if( !( target == BST ) )
         {
             target->rightChild = newNode->leftChidld;    //*newNode 的左子树接到 *target 的右子树上
         }
         else
         {
             target->leftChidld = newNode->leftChidld;    //*newNode 的左子树接到 *target 的左子树上
         }
         delete newNode;                    //删除结点 *newNode
     }
 }

 //注意 while 循环体：
 //如果 BST 左子树为空，则 while 循环体不执行，那么 target 就不会发生改变。
 //然而一开始 target == BST。
 //反过来说，如果 BST 左子树不为空，则 while 执行，那么 target 就会发生改变。
 //target 改变了，就和 BST 不一样。
 //所以就可以表明 BST 左子树非空。

 void BSTree::removeNode2( _BSTree &BST )
 {
     BSTNode *target = NULL;
     if( !BST->leftChidld )
     {
         target = BST;
         BST = BST->rightChild;
         delete target;
     }
     else if( !BST->rightChild )
     {
         target = BST;
         BST = BST->leftChidld;
         delete target;
     }
     else
     {
         BSTNode *newNode = NULL;
         target = BST;
         newNode = BST->rightChild;        //右子树根结点
         while( newNode->leftChidld )    //寻找 BST 结点的中序前驱结点，即以 BST->leftChild为根结点的子树中的最左结点
         {
             target = newNode;            //*target 指向 *BST 的父结点
             newNode = newNode->leftChidld;        //*newNode 指向 *BST 的中序后继结点
         }
         BST->data = newNode->data;        //*newNode 的数据传給 *BST 的数据，然后删除结点 *newNode
         if( target != BST )                //BST->leftChidld 的左子树非空，这句话等价于 if( !( target == BST ) )
         {
             target->leftChidld = newNode->rightChild;        //*newNode 的右子树接到 *target 的左子树上
         }
         else
         {
             target->rightChild = newNode->rightChild;        //*newNode 的右子树接到 *target 的右子树上
         }
         delete newNode;                    //删除结点 *newNode
     }
 }

 //注意 while 循环体：
 //如果 BST 右子树为空，则 while 循环体不执行，那么 target 就不会发生改变。
 //然而一开始 target == BST。
 //反过来说，如果 BST 右子树不为空，则 while 执行，那么 target 就会发生改变。
 //target 改变了，就和 BST 不一样
 //所以就可以表明 BST 右子树非空。

 void BSTree::removeNode3( _BSTree &BST )
 {
     BSTNode *target = NULL;
     if( !BST->leftChidld )
     {
         target = BST;
         BST = BST->rightChild;
         delete target;
     }
     else if( !BST->rightChild )
     {
         target = BST;
         BST = BST->leftChidld;
         delete target;
     }
     else
     {
         BSTNode *newNode = NULL;
         target = BST;
         newNode = BST->leftChidld;            //左子树根结点
         while( newNode->rightChild )        //寻找 BST 结点的中序前驱结点，即以 BST->leftChild为根结点的子树中的最右结点
         {
             //target = newNode;
             newNode = newNode->rightChild;
         }
         newNode->rightChild = target->leftChidld;        //*target 的左子树接到 *newNode 的左子树上
         target = target->leftChidld;                    //*target 的左子树接到父结点上
         delete target;                    //删除结点 *target
     }
 }

 // BinarySearchTree.cpp : Defines the entry point for the console application.
 //

 #include "stdafx.h"
 #include "BSTree.h"

 //这是EasyX的官方网站： https://www.easyx.cn/

 void test1()
 {
     HANDLE hOut; 

     //  获取输出流的句柄
     hOut = GetStdHandle(STD_OUTPUT_HANDLE);

     BSTree BST1;
     elementType value;
     vector<elementType>VI;
     while( cin >> value )
     {
         if( (char)value == '#' && value != /*-999*/ ) //细节处理：一定要加 && value != 35，因为 # 的ASCII码是35，
         {                                                //不加的话在输入数字“35”而不是“#”时循环也会终止
             break;
         }
         else
         {
             VI.push_back(value);
         }

     }
     BST1.createBinarySearchTree( BST1.getRootNode(), VI );

     SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED | // 前景色_红色
                             FOREGROUND_BLUE |// 前景色_蓝色
                             FOREGROUND_INTENSITY);// 加强

     cout << "PreOrder:" << endl;
     BST1.preOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "InOrder:" << endl;
     BST1.inOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "PostOrder:" << endl;
     BST1.postOrderTraversal( BST1.getRootNode() );
     cout << endl;

     SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED |   // 前景色_红色
                             FOREGROUND_GREEN | // 前景色_绿色
                             FOREGROUND_BLUE ); // 前景色_蓝色

     return;
 }

 void test2()
 {
     HANDLE hOut; 

     //  获取输出流的句柄
     hOut = GetStdHandle(STD_OUTPUT_HANDLE);  

     BSTree BST1;
     elementType value;
     vector<elementType>VI;

     while( cin >> value )
     {
         if( (char)value == '#' && value != /*-999*/ ) //细节处理：一定要加 && value != 35，因为 # 的ASCII码是35，
         {                                                //不加的话在输入数字“35”而不是“#”时循环也会终止
             break;
         }
         else
         {
             VI.push_back(value);
         }

     }

     BST1.createBinarySearchTree( BST1.getRootNode(), VI );

     _BSTree index = NULL;    

     SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED | // 前景色_红色
                             FOREGROUND_BLUE |// 前景色_蓝色
                             FOREGROUND_INTENSITY);// 加强

     cout << "PreOrder:" << endl;

     BST1.preOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "InOrder:" << endl;
     BST1.inOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "PostOrder:" << endl;
     BST1.postOrderTraversal( BST1.getRootNode() );
     cout << endl;

     //elementType key = ;// = 545;
     //下面这句话不会运行
     //cin >> key;

     elementType Arr[] = { , , , , , ,  };

     for( int j = ; j < sizeof(Arr) / sizeof(elementType); j ++ )
     {
         if( BST1.search( BST1.getRootNode(), Arr[j], index ) )
         {
             SetConsoleTextAttribute(hOut,
                             FOREGROUND_BLUE |      // 前景色_蓝色
                             FOREGROUND_INTENSITY ); // 前景色_加强
             cout << Arr[j] << " is in the binary search tree." << endl;
             SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED |   // 前景色_红色
                             FOREGROUND_GREEN | // 前景色_绿色
                             FOREGROUND_BLUE ); // 前景色_蓝色
         }
         else
         {
             SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED |       // 前景色_红色
                             FOREGROUND_INTENSITY ); // 前景色_加强
             cout << Arr[j] << " is not in the binary search tree." << endl;
             SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED |   // 前景色_红色
                             FOREGROUND_GREEN | // 前景色_绿色
                             FOREGROUND_BLUE ); // 前景色_蓝色
         }
     }

     //无法实现下面这样输入数值判断其是否存在
     /*
     BSTNode *father = NULL, *target = NULL;

     elementType key;
     while( cin >> key )
     {
         //target = NULL;
         if( (char)key == '#' && key != 35 )
         {
             break;
         }
         else
             target = BST1.search( BST1.getRootNode(), key, father );

         if(!target)
         {
             cout << "No!" << endl;
         }
         else
         {
             cout << "Yes!" << endl;
         }

     }
     */    

     return;
 }

 void test3()
 {
     HANDLE hOut; 

     //  获取输出流的句柄
     hOut = GetStdHandle(STD_OUTPUT_HANDLE);  

     BSTree BST1;
     elementType value;
     vector<elementType>VI;

     while( cin >> value )
     {
         if( (char)value == '#' && value != /*-999*/ ) //细节处理：一定要加 && value != 35，因为 # 的ASCII码是35，
         {                                                //不加的话在输入数字“35”而不是“#”时循环也会终止
             break;
         }
         else
         {
             VI.push_back(value);
         }

     }

     BST1.createBinarySearchTree( BST1.getRootNode(), VI );

     _BSTree index = NULL;    

     SetConsoleTextAttribute(hOut,
                             FOREGROUND_BLUE |      // 前景色_蓝色
                             FOREGROUND_INTENSITY ); // 前景色_加强
     cout << "The origin binary search tree is as follow:" << endl;
     SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED | // 前景色_红色
                             FOREGROUND_BLUE |// 前景色_蓝色
                             FOREGROUND_INTENSITY);// 加强

     cout << "PreOrder:" << endl;

     BST1.preOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "InOrder:" << endl;
     BST1.inOrderTraversal( BST1.getRootNode() );
     cout << endl;
     cout << "PostOrder:" << endl;
     BST1.postOrderTraversal( BST1.getRootNode() );

     cout << endl;

     elementType Arr[] = { , ,  };
     for( int i = ; i < sizeof(Arr) / sizeof(elementType); i ++ )
     {
         _BSTree index = BST1.getRootNode();
         //BST1.deleteNode1( index, Arr[i] );
         BST1.deleteNode2( index, Arr[i] );
         SetConsoleTextAttribute(hOut,
                             FOREGROUND_BLUE |      // 前景色_蓝色
                             FOREGROUND_INTENSITY ); // 前景色_加强
         cout << "After deleting node " << Arr[i] << ", the current binary search tree is as follow:"<< endl;

         SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED | // 前景色_红色
                             FOREGROUND_BLUE |// 前景色_蓝色
                             FOREGROUND_INTENSITY);// 加强

         cout << "PreOrder:" << endl;

         BST1.preOrderTraversal( BST1.getRootNode() );
         cout << endl;
         cout << "InOrder:" << endl;
         BST1.inOrderTraversal( BST1.getRootNode() );
         cout << endl;
         cout << "PostOrder:" << endl;
         BST1.postOrderTraversal( BST1.getRootNode() );
         cout << endl;

     }
     SetConsoleTextAttribute(hOut,
                             FOREGROUND_RED |   // 前景色_红色
                             FOREGROUND_GREEN | // 前景色_绿色
                             FOREGROUND_BLUE ); // 前景色_蓝色
     return;
 }

 int main(int argc, char* argv[])
 {
     //test1();
     //test2();
     test3();
     return ;
 }

AVL树：

 // Tips for Getting Started:
 //   1. Use the Solution Explorer window to add/manage files
 //   2. Use the Team Explorer window to connect to source control
 //   3. Use the Output window to see build output and other messages
 //   4. Use the Error List window to view errors
 //   5. Go to Project > Add New Item to create new code files, or Project > Add Existing Item to add existing code files to the project
 //   6. In the future, to open this project again, go to File > Open > Project and select the .sln file

 #ifndef PCH_H
 #define PCH_H

 #include <iostream>
 #include <algorithm>
 #include <graphics.h>
 #include <windows.h>

 using namespace std;

 // TODO: add headers that you want to pre-compile here

 #endif //PCH_H

 #pragma once
 /* AVL node */
 template <class T>
 class AVLNode
 {
 public:
     T key;
     int balance;
     AVLNode *leftChild, *rightChild, *parent;

     AVLNode(T k, AVLNode *p) : key(k), balance(), parent(p),leftChild(NULL), rightChild(NULL) {}
     ~AVLNode();
 };

 #pragma once
 /* AVL tree */

 #include "AVLnode.h"
 template <class T>
 class AVLTree
 {
 public:
     AVLTree(void);
     ~AVLTree(void);
     bool insert(T key);
     void deleteKey(const T key);
     void printBalance();
     void inOrderTraverse();
     void preOrderTraverse();
     void postOrderTraverse();
     void display();

     AVLNode<T>* RR_Rotate(AVLNode<T> *AVLB);        //rotate left
                                                     //当在RR发生不平衡时需要进行左旋转
     AVLNode<T>* LL_Rotate(AVLNode<T> *AVLB);        //rotate right
                                                     //当在LL发生不平衡时需要进行右旋转
     AVLNode<T>* LR_Rotate(AVLNode<T> *AVLB);    //rotate left then right
     AVLNode<T>* RL_Rotate(AVLNode<T> *AVLB);    //rotate right then left
     AVLNode<T>* getRootNode();
     void reBalance(AVLNode<T> *AVLB);
     int height(AVLNode<T> *AVLB);
     void setBalance(AVLNode<T> *AVLB);
     void printBalance(AVLNode<T> *AVLB);
     void clearNode(AVLNode<T> *AVLB);
     void inOrderTraverse(AVLNode<T> *AVLB);
     void preOrderTraverse(AVLNode<T> *AVLB);
     void postOrderTraverse(AVLNode<T> *AVLB);

     void display(AVLNode <T>*AVLB, int space, int colour);

 private:
     AVLNode<T> *root;
 };

 #include "pch.h"
 #include "AVLnode.h"

 template <class T>
 AVLNode<T>::~AVLNode()
 {
     delete leftChild;
     delete rightChild;
 }

 #include "pch.h"
 #include "AVLtree.h"

 template <class T>
 void AVLTree<T>::reBalance(AVLNode<T> *AVLB)
 {
     setBalance(AVLB);

     if (AVLB->balance == -)
     {
         if (height(AVLB->leftChild->leftChild) >= height(AVLB->leftChild->rightChild))
             AVLB = LL_Rotate(AVLB);
         else
             AVLB = LR_Rotate(AVLB);
     }
     else if (AVLB->balance == )
     {
         if (height(AVLB->rightChild->rightChild) >= height(AVLB->rightChild->leftChild))
             AVLB = RR_Rotate(AVLB);
         else
             AVLB = RL_Rotate(AVLB);
     }

     if (AVLB->parent != NULL)
     {
         reBalance(AVLB->parent);
     }
     else
     {
         root = AVLB;
     }
 }

 template <class T>
 AVLNode<T>* AVLTree<T>::RR_Rotate(AVLNode<T> *AVLB)
 {
     AVLNode<T> *tmp = AVLB->rightChild;
     tmp->parent = AVLB->parent;
     AVLB->rightChild = tmp->leftChild;

     if (AVLB->rightChild != NULL)
         AVLB->rightChild->parent = AVLB;

     tmp->leftChild = AVLB;
     AVLB->parent = tmp;

     if (tmp->parent != NULL)
     {
         if (tmp->parent->rightChild == AVLB)
         {
             tmp->parent->rightChild = tmp;
         }
         else
         {
             tmp->parent->leftChild = tmp;
         }
     }

     setBalance(AVLB);
     setBalance(tmp);
     return tmp;
 }

 template <class T>
 AVLNode<T>* AVLTree<T>::LL_Rotate(AVLNode<T> *AVLB)
 {
     AVLNode<T> *tmp = AVLB->leftChild;
     tmp->parent = AVLB->parent;
     AVLB->leftChild = tmp->rightChild;

     if (AVLB->leftChild != NULL)
         AVLB->leftChild->parent = AVLB;

     tmp->rightChild = AVLB;
     AVLB->parent = tmp;

     if (tmp->parent != NULL)
     {
         if (tmp->parent->rightChild == AVLB)
         {
             tmp->parent->rightChild = tmp;
         }
         else
         {
             tmp->parent->leftChild = tmp;
         }
     }

     setBalance(AVLB);
     setBalance(tmp);
     return tmp;
 }

 template <class T>
 AVLNode<T>* AVLTree<T>::LR_Rotate(AVLNode<T> *AVLB)
 {
     AVLB->leftChild = RR_Rotate(AVLB->leftChild);
     return LL_Rotate(AVLB);
 }

 template <class T>
 AVLNode<T>* AVLTree<T>::RL_Rotate(AVLNode<T> *AVLB)
 {
     AVLB->rightChild = LL_Rotate(AVLB->rightChild);
     return RR_Rotate(AVLB);
 }

 template <class T>
 AVLNode<T>* AVLTree<T>::getRootNode()
 {
     return root;
 }

 template <class T>
 int AVLTree<T>::height(AVLNode<T> *AVLB)
 {
     if (AVLB == NULL)
         return -;
     return  + max(height(AVLB->leftChild), height(AVLB->rightChild));
 }

 template <class T>
 void AVLTree<T>::setBalance(AVLNode<T> *AVLB)
 {
     AVLB->balance = height(AVLB->rightChild) - height(AVLB->leftChild);
 }

 template <class T>
 void AVLTree<T>::printBalance(AVLNode<T> *AVLB)
 {
     ios::sync_with_stdio(false);
     if (AVLB != NULL)
     {
         printBalance(AVLB->leftChild);
         cout << AVLB->balance << " ";
         //std::cout << n->key << " ";
         printBalance(AVLB->rightChild);
     }
 }

 template <class T>
 void AVLTree<T>::inOrderTraverse(AVLNode<T> *AVLB)
 {
     ios::sync_with_stdio(false);
     if (AVLB)
     {
         inOrderTraverse(AVLB->leftChild);
         cout << AVLB->key << " ";
         inOrderTraverse(AVLB->rightChild);
     }
 }

 template <class T>
 void AVLTree<T>::preOrderTraverse(AVLNode<T> *AVLB)
 {
     if (AVLB)
     {
         cout << AVLB->key << " ";
         preOrderTraverse(AVLB->leftChild);
         preOrderTraverse(AVLB->rightChild);
     }
 }

 template <class T>
 void AVLTree<T>::postOrderTraverse(AVLNode<T> *AVLB)
 {
     ios::sync_with_stdio(false);
     if (AVLB)
     {
         postOrderTraverse(AVLB->leftChild);
         postOrderTraverse(AVLB->rightChild);
         cout << AVLB->key << " ";
     }
 }

 template <class T>
 void AVLTree<T>::display(AVLNode <T>*AVLB, int space, int colour )
 {
     ios::sync_with_stdio(false);
     HANDLE  hConsole;
     hConsole = GetStdHandle(STD_OUTPUT_HANDLE);
     if (AVLB)
     {
         display(AVLB->rightChild, space + , colour + );
         SetConsoleTextAttribute(hConsole, 0x0008 | colour);
         //colour++;
         cout << endl;
         if (AVLB == root)
             cout << " Root ----> ";
         for (int i = ; i < space && AVLB != root; i++)
             cout << "          ";
         cout << AVLB->key;
         display(AVLB->leftChild, space + , colour + );
     }
 }

 template <class T>
 AVLTree<T>::AVLTree(void) : root(NULL) {}

 template <class T>
 AVLTree<T>::~AVLTree(void)
 {
     delete root;
 }

 template <class T>
 bool AVLTree<T>::insert(T key)
 {
     if (root == NULL)
     {
         root = new AVLNode<T>(key, NULL);
     }
     else
     {
         AVLNode<T>  //这种风格我觉得不错
                     //I appreciate this style of code
             *target = root,
             *parent;

         while ()
         {
             if (target->key == key)
                 return false;

             parent = target;

             bool goLeft = target->key > key;
             target = goLeft ? target->leftChild : target->rightChild;

             if (target == NULL)
             {
                 if (goLeft)
                 {
                     parent->leftChild = new AVLNode<T>(key, parent);
                 }
                 else
                 {
                     parent->rightChild = new AVLNode<T>(key, parent);
                 }

                 reBalance(parent);
                 break;
             }
         }
     }

     return true;
 }

 template <class T>
 void AVLTree<T>::deleteKey(const T delKey)
 {
     if (root == NULL)
         return;

     AVLNode<T>
         *target = root,
         *parent = root,
         *delNode = NULL,
         *child = root;

     while (child != NULL)
     {
         parent = target;
         target = child;
         child = delKey >= target->key ? target->rightChild : target->leftChild;
         if (delKey == target->key)
             delNode = target;
     }

     if (delNode != NULL)
     {
         delNode->key = target->key;

         child = target->leftChild != NULL ? target->leftChild : target->rightChild;

         if (root->key == delKey)
         {
             root = child;
         }
         else
         {
             if (parent->leftChild == target)
             {
                 parent->leftChild = child;
             }
             else
             {
                 parent->rightChild = child;
             }

             reBalance(parent);
         }
     }
 }

 template <class T>
 void AVLTree<T>::printBalance()
 {
     ios::sync_with_stdio(false);
     printBalance(root);
     cout << endl;
 }

 template <class T>
 void AVLTree<T>::inOrderTraverse()
 {
     ios::sync_with_stdio(false);
     inOrderTraverse(root);
     cout << endl;
 }

 template <class T>
 void AVLTree<T>::preOrderTraverse()
 {
     ios::sync_with_stdio(false);
     preOrderTraverse(root);
     cout << endl;
 }

 template <class T>
 void AVLTree<T>::postOrderTraverse()
 {
     ios::sync_with_stdio(false);
     postOrderTraverse(root);
     cout << endl;
 }

 template <class T>
 void AVLTree<T>::display()
 {
     ios::sync_with_stdio(false);
     int color = ;
     display(root, , color);
     cout << endl;
 }

 // AVL_2.cpp : This file contains the 'main' function. Program execution begins and ends there.
 //

 #include "pch.h"
 #include <iostream>
 #include "AVLtree.h"
 #include "AVLnode.h"
 #include "AVLnode.cpp"
 #include "AVLtree.cpp"

 int main()
 {
     //std::cout << "Hello World!\n";
     ios::sync_with_stdio(false);
     AVLTree<int> AVLBT;
     HANDLE  hConsole;
     hConsole = GetStdHandle(STD_OUTPUT_HANDLE);
     cout << "Inserting integer values 1 to 26" << std::endl;
     int Arr[] = { ,,,,,,,,,,,,,,,,,,,,,
         ,,, };
     for (int i = ; i < sizeof(Arr) / sizeof(int); i++)
     //for( int i = 0; Arr[i] != 0; i ++ )
         //AVLBT.insert(i);
         AVLBT.insert(Arr[i]);

     cout << "Printing the balance factor of each node: " << std::endl;
     SetConsoleTextAttribute(hConsole, );
     AVLBT.printBalance();
     SetConsoleTextAttribute(hConsole, );
     cout << "Printing key: " << std::endl;
     SetConsoleTextAttribute(hConsole, 0x0008 | );
     AVLBT.inOrderTraverse();
     AVLBT.display();
     //AVLTree<int> *root = avl.getRootNode();
     while ()
     {
         SetConsoleTextAttribute(hConsole, );
         cout << "\n---------------------" << endl;
         cout << "AVL tree implementation" << endl;
         cout << "By Utah Xef developed" << endl;
         cout << "\n---------------------" << endl;
         cout << "1.insert element into the tree" << endl;
         cout << "2.display balanced AVL tree" << endl;
         cout << "3.preorder traversal" << endl;
         cout << "4.inorder traversal" << endl;
         cout << "5.postorder traversal" << endl;
         cout << "6.delete key" << endl;
         cout << "7.display the balance factor of each node" << endl;
         cout << "8.exit" << endl;
         cout << "enter your choice: ";
         int choice;
         cin >> choice;

         switch (choice)

         {

         case :

             cout << "enter value to be inserted: ";
             int item;
             cin >> item;

             AVLBT.insert(item);

             break;

         case :

             if (AVLBT.getRootNode() == nullptr)

             {

                 cout << "tree is empty" << endl;

                 continue;

             }

             cout << "balanced avl tree:" << endl;

             AVLBT.display();

             break;

         case :

             cout << "preorder traversal:" << endl;
             SetConsoleTextAttribute(hConsole, 0x0008 | );
             AVLBT.preOrderTraverse();

             cout << endl;

             break;
         case :

             cout << "inorder traversal:" << endl;
             SetConsoleTextAttribute(hConsole, 0x0008 | );
             AVLBT.inOrderTraverse();

             cout << endl;

             break;

         case :

             cout << "postorder traversal:" << endl;
             SetConsoleTextAttribute(hConsole, 0x0008 | );
             AVLBT.postOrderTraverse();

             cout << endl;

             break;

         case :
             int value;
             cout << "Please input the value to delete:" << endl;
             cin >> value;
             AVLBT.deleteKey(value);
             break;

         case :
             cout << "The balance factor of each node:" << endl;
             SetConsoleTextAttribute(hConsole, 0x0008 | );
             AVLBT.printBalance();
             break;
         case :
             exit();

             break;
         default:

             cout << "Wrong choice" << endl;
             break;
         }

     }
     //std::cout << std::endl;
     std::cin.get();
 }

 // Run program: Ctrl + F5 or Debug > Start Without Debugging menu
 // Debug program: F5 or Debug > Start Debugging menu

 // Tips for Getting Started:
 //   1. Use the Solution Explorer window to add/manage files
 //   2. Use the Team Explorer window to connect to source control
 //   3. Use the Output window to see build output and other messages
 //   4. Use the Error List window to view errors
 //   5. Go to Project > Add New Item to create new code files, or Project > Add Existing Item to add existing code files to the project
 //   6. In the future, to open this project again, go to File > Open > Project and select the .sln file