算法（1）：查找&排序

算法（Algorithm）：一个计算过程，解决问题的方法

程序 = 数据结构+算法

时间复杂度：

当算法过程中出现循环折半的时候，复杂度式子中会出现 O(logn)

时间复杂度小结：
　　1. 时间复杂度是用来估计算法运行时间的一个式子（是一个单位）
　　2. 一般来说，时间复杂度高的算法比复杂度低的算法慢
　　3. 常见的时间复杂度（按效率排序）：
　　　　O(1)<O(logn)<O(n)<O(nlogn)<O(n的平方)<O(n的平方logn)<O(n的立方)
　　4. 复杂问题的时间复杂度：
　　　　O(n!) O(2的n次方) O(n的n次方)

简单判断算法复杂度的方法：
快速判断算法复杂度（适用天绝大多数简单情况）：
　　-  确实问题规模n
　　-  循环减半过程 -> logn
　　-  k层关于n的循环 -> n的k次方
复杂情况：根据算法执行过程判断

空间复杂度

空间复杂度：用来 评估算法内存占用大小的式子空间复杂度的表示方式和时间复杂度完全一样：
　　-  算法使用了几个变量：O(1)
　　-  算法使用了长度为n的一维列表：O(n)
　　-  算法使用了m行n列的二维列表：O(mn)
“空间换时间” （时间比空间重要）

递归：

递归的两个特点：
　　-  调用自身
　　-  结束条件

汉诺塔：

移动顺序：

def hanoi(n,a,b,c): # n表示n个盘子，a、b、c表示从a经过b移动到c
    if n>0:
        hanoi(n-1,a,c,b)
        print("moving from %s to %s"%(a,c))
        hanoi(n-1,b,a,c)

移动次数：

　　h(n)=2h(n-1)+1

查找：

查找：在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程

列表查找（线性表查找）：

线性查找： 从列表中查找指定元素

　　- 输入：列表、待查找元素

　　- 输出：元素下标（未找到元素时一般返回None或-1）
内置列表查找函数：index()

顺序查找：也称线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止
时间复杂度：O(n)

代码：

def linear_search(li,val):
    for ind,v in enumerate(li):
        if v == val:
            return ind
    else:
        return None

二分查找：

二分查找（Binary Search）：又称折半查找，从【有序】列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半
时间复杂度： O(logn)
代码：

def binary_search(li,val):
    left = 0
    right = len(li)-1
    while left <= right:  # 候选区有值
        mid = (left+right)//2
        if li[mid] == val:
            return mid
        elif li[mid] > val:
            right = mid - 1
        else:
            left = left+1
    else:
        return None

注：列表的内置函数index()用的是 线性查找

列表排序：

排序：将一组“无序”的记录序列调整为“有序”的记录序列
列表排序：将无序列表变为有序列表
　　- 输入：列表
　　- 输出：有序列表
升序和降序
内置排序函数：sort()

常见排序算法：

冒泡排序、选择排序、插入排序
快速排序、堆排序、归并排序
希尔排序、计数排序、基数排序

冒泡排序（Bubble Sort）：

列表每两个相邻的数，如果前面比后面大，则交换这两个数
一趟排序完成后，则无序区减少一个数，有序区增加一个数
代码关键点：趟、无序区范围
时间复杂度：O(n的平方)
代码：

def bubble_sort(li):
    for i in range(len(li)-i): # 第i趟
        exchange = False  # 用于标识一趟中是否发生了位置互换
        for j in range(len(li)-1-i): # 指针移动
            if li[j]>li[j+1]: # 升序排序
                li[j],li[j+1] = li[j+1],li[j]  # 交换位置
                exchange = True
        if not exchange:  # 如果这一趟没有发生位置互换，意味着已经全部排序好了，下面的趟也就不用再进行了
            return

选择排序（Select Sort）:

　　一趟排序记录最小的数，放到第一个位置
　　再一趟排序记录下列表无序区最小的数，放到第二个位置
　　...（以此类推）
算法关键点：有序区和无序区、无序区最小数的位置
时间复杂度：O(n的平方)
代码：

def select_sort(li):
    for i in range(len(li)-1):  # 第i趟
        min_loc = i  # 记录最小值的位置（索引）
        for j in range(i+1,len(li)):  # 查找无序区的最小值
            if li[j] < li[min_loc]:
                min_loc = j  # 最小值的位置更改为j
        if i != min_loc:
            li[i],li[min_loc] = li[min_loc],li[i]  # 互换位置

插入排序（Insert Sort）：

初始时手里（有序区）只有一张牌，每次（从无序区）摸一张牌，插入到手里已有牌的正确位置
时间复杂度： O(n的平方)

代码：

def insert_sort(li):
    for i in range(1,len(li)): # i表示抽出来的牌的下标
        temp = li[i]
        j = i - 1  # j 表示有序区牌的下标
        while j>=0 and li[j] > temp:
            li[j+1] = li[j]  # 往右移
            j -= 1 # 下标左移
        li[j+1] = temp

快速排序：

快速排序：快
思路：
　　-  取一个元素p（第一个元素），使元素p归位；
　　-  列表被p分成两部分，左边都比p小，右边都比p大；
　　-  递归完成排序

代码：

def partition(li,left,right):
    """先让一个数归位（如左边第一个），然后把小于归位数的放到其左边，大于归位数的放到其右边"""
    temp = li[left]
    while left < right:
        while left < right and li[right] >= temp: # 从右边找比temp小的数
            right -= 1 # 这个数如果不比 temp小，则让 right 往左移一步
        li[left] = li[right]  # 把右边的值写到左边空位上
        while left < right and li[left] <= temp:
            left += 1
        li[right] = li[left]  # 把左边的值写到右边空位上
    li[left] = temp   # 把temp归位  # 循环结束时， left==right
    return left
 
def quick_sort(li,left,right):
    if left < right:  # 至少两个元素
        mid = partition(li,left,right)
        quick_sort(li,left,mid-1) # 递归
        quick_sort(li,mid+1,right)

快速查询的效率：
　　时间复杂度： O(nlogn)
快速排序的问题：
　　- 最坏情况
　　- 递归（耗资源）

堆排序：

树与二叉树：

树是一种数据结构， 比如：目录结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合：
　　-  如果n=0,那这是一棵空树；
　　-  如果 n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树

一些概念：

根节点 和 叶子节点（末端、没有分叉的节点即叶子节点）
树的深度（高度）：最深有几层
节点的度：该节点下面分了几个叉，就代表它的度
树的度：整个树中分的最多的叉（度最多的节点）
孩子节点/父节点
子树：类似 一个大树上掰下来一个树枝，就是一个子树

二叉树：

二叉树：度不超过2的树
每个节点最多有两个孩子节点
两个孩子节点被区分为左孩子节点和右孩子节点
 
满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树
 
完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

二叉树的存储方式（表示方式）：
　　- 链式存储方式
　　- 顺序存储方式

二叉树的顺序存储方式：

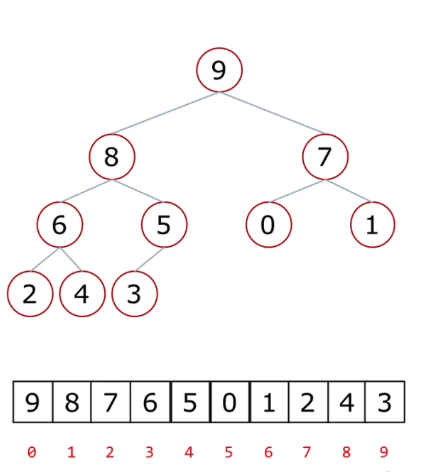
父节点和左孩子节点的编号下标有什么关系 ？
    - i -> 2i+1
父节点的右孩子节点的编号下标有什么关系？
    - i -> 2i+2

堆：

堆：一种特殊的完全二叉树结构
    - 大根堆： 一棵完全二叉树，满足任一节点都比其孩子节点大
    - 小根堆： 一棵完全二叉树，满足任一节点都比其孩子节点小
    

堆的向下调整：

假设：节点的左右子树都是堆，但自身不是堆； 当根节点的左右子树都是堆时，可以通过一次向下的调整来将其变换成一个堆

堆排序：

思路：

堆排序过程：
1. 建立堆
2. 得到堆顶元素，为最大元素
3. 去掉堆顶将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序
4. 堆顶元素为第二大元素
5. 重复步骤3，直到堆变空  
堆排序的时间复杂度：O(nlogn)

示例代码：

# 向下调整函数的实现
# 假设节点的左右子树都是堆，但自身不是堆；当根节点的左右子树都是堆时，可以通过一次向下的调整来将其变成一个堆
 
def sift(li, low, high):
    """
    节点的左右子树都是堆，但自身不是堆；通过该 sift() 的调整变成堆
    :param li: 列表（待处理的“堆”）
    :param low: 堆的根节点位置（列表的索引）
    :param high: 堆最后一个元素的位置
    :return:
    """
    i = low  # 堆的父节点
    j = 2 * i + 1  # i 的左子节点
    temp = li[low]  # 把堆顶存起来
    while j <= high:  # 子节点没有超出列表的最大索引
        if j + 1 <= high and li[j + 1] > li[j]:  # 如果有右子节点，比较左右两个子节点哪个大
            j = j + 1  # j 指向右子节点
        if li[j] > temp:
            li[i] = li[j]  # 如果子节点比父节点大，就把子节点移到父节点的位置（不用把父节点移到子节点的位置，因为该temp还需要和下面的子节点继续比较大小）
            i = j  # 把上次的子节点当作下次比较的父节点
            j = 2 * i + 1
        else:
            li[i] = temp  # 如果子节点比父节点（temp）小，再把temp放到父节点的位置,同时退出循环
            break
    else:  # 上面的循环如果能正常走完，说明上面的 while 循环没有被 break （即子节点一直都比父节点大），走 else 时已经是走到了最后一层
        li[i] = temp
 
def heap_sort(li):
    n = len(li)
    for i in range((n - 2) // 2, -1, -1):
        # i 指的是 建堆的时候调整的部分堆的根的下标
        """
        从 (n-1)//2 的位置 倒序（每次减1）到 -1的位置；
        j = 2*i + 1 ==> i = (j-1)/2 ； 又因为 n为 列表的长度，所以最后一个元素的 索引为 n-1；取整是因为最后一个既有可能是左子节点也有可能是右子节点
        """
        sift(li, i, n - 1)  # 用列表的长度减1作为 high 参数； high 的作用就是不让子节点越界
        # 通过上面的 sift() 堆已经建成
 
    # 开始调整堆
    for i in range(n - 1, -1, -1):
        # i 表示堆的最后一个位置
        li[0], li[i] = li[i], li[0]  # 调整位置：最后一个元素和堆顶互换
        sift(li, 0, i - 1)  # 再重新建堆 ； i-1 是新的 high（堆顶元素已经放到了列表最后一个位置，不在计算范围之内）
 
li = [i for i in range(30)]
import random
random.shuffle(li)
print(li)
 
heap_sort(li)
print(li)

堆排序的 topk 问题：

# topk 问题： 现在有n个数，设计算法得到前k大的数（k<n）
 
"""
利用堆排序解决 topk 问题的思路：
1. 取列表前k个元素建立一个小根堆；堆顶就是目前第k大的数
2. 依次向后遍历原列表，对于列表中的元素，如果小于堆顶，慢忽略该元素；如果大于堆顶，则将堆顶换成该元素，并且对堆进行一次调整
3. 遍历列表所有元素后，倒序弹出堆顶
利用堆排序解决 topk 问题的时间复杂度： O(nlogk)
"""
 
def sift(li, low, high):
    """
    调整为小根堆：第一个元素最小
    :param li: 列表（待处理的“堆”）
    :param low: 堆的根节点位置（列表的索引）
    :param high: 堆最后一个元素的位置
    :return:
    """
    i = low
    j = 2 * i + 1
    temp = li[low]  # 把堆顶存起来
    while j <= high:  # 子节点没有超出列表的最大索引
        if j + 1 <= high and li[j + 1] < li[j]:  # 如果有右子节点，比较左右两个子节点哪个小
            j = j + 1  # j 指向右子节点
        if li[j] < temp:
            li[i] = li[j]  # 如果子节点比父节点大，就把子节点移到父节点的位置（不用把父节点移到子节点的位置，因为该temp还需要和下面的子节点继续比较大小）
            i = j  # 把上次的子节点当作下次比较的父节点
            j = 2 * i + 1
        else:
            li[i] = temp  # 如果子节点比父节点（temp）小，再把temp放到父节点的位置,同时退出循环
            break
    else:  # 上面的循环如果能正常走完，说明上面的 while 循环没有被 break （即子节点一直都比父节点大），走 else 时已经是走到了最后一层
        li[i] = temp
 
def topk(li,k):
    heap = li[0:k]
    n = len(li)
    for i in  range((k-2)//2,-1,-1):
        # i 表示父节点
        sift(heap,i,k-1)
    for i in range(k,n):
        if li[i] > heap[0]: # li列表后面的元素和堆顶做比较
            heap[0] = li[i]
            sift(heap,0,k-1)
 
    # 对 heap 中的元素进行排序
    for i in range(k-1,-1,-1):
        # i 表示最后一个元素的位置
        heap[0],heap[i] = heap[i],heap[0]
        sift(heap,0,i-1)
    return heap
 
li = [i for i in range(30)]
 
import random
random.shuffle(li)
print(li)
print(topk(li,10))

归并排序：（merge）

假设现在的列表分两段有序，将其合成为一个有序列表，这种操作称为一次归并

归并排序的思路：

1. 分解：将列表越分越小，直至分成一个元素
2. 终止条件： 一个元素是有序的
3. 合并：将两个有序列表归并，列表越来越大

示例代码：

def merge(li,low,mid,high):
    """一次归并"""
    i = low
    j = mid + 1
    temp = []
    while i <= mid and j <= high:
        if li[i] <= li[j]:
            temp.append(li[i])
            i += 1
        else:
            temp.append(li[j])
            j += 1
    # 总有一边的数会先走完
    while i <= mid:
        temp.append(li[i])
        i += 1
    while j <= high:
        temp.append(li[j])
        j += 1
 
    li[low:high+1] = temp  # 把 temp 赋值给 li的 low~high 部分（low不是从0开始）
 
def merge_sort(li,low,high):
    if low < high:  # 此时至少有两个元素
        mid = (low+high)//2  # 取中间位置（这个也是循环条件）
        merge_sort(li,low,mid)  # 把左边的分解、排序
        merge_sort(li,mid+1,high)  # 把右边的分解、排序
        merge(li,low,mid,high)  # 递归的时候把上面分解的列表元素一次次进行归并
 
li = list(range(100))
import random
random.shuffle(li)
print(li)
 
merge_sort(li,0,len(li)-1)
print("li",li)

归并排序的时间复杂度：O(nlogn)
空间复杂度：O(n) # 前面几种排序方式都是“原地排序”（没有建新的列表），但归并排序不是“原地排序”；另外 python 的sort方法就是基于“归并排序”实现的（因为归并排序是稳定式的排序）

快速排序、归并排序和堆排序小结：

1. 三种排序算法的时间复杂度都是 O(nlogn)
2. 一般情况下，就运行时间而言： 快速排序 < 归并排序 < 堆排序
3. 三种排序算法的缺点：
    快速排序：极端情况下排序效率低
    归并排序：需要额外的内存开销
    堆排序： 在快的排序中相对较慢