JAVA基础——生产者消费者问题

1.生产者消费者问题：经典案例

生产者和消费者问题是操作系统的经典问题，在实际工作中也常会用到，主要的难点在于协调生产者和消费者，因为生产者的个数和消费者的个数不确定，而生产者的生成速度与消费者的消费速度也不一样，同时还要实现生产者与消费者的解耦，即生产者并不知道有哪些消费者，而消费者也不需要知道产品是哪个生产的，他们之间只与一个交易平台发生关系。

产生的原因：为了解决集合在线程中的使用

2.主要方法

Object（基类）:

1. wait():等待 ：当缓冲区已满/空时，生产者/消费者线程停止自己的执行，放弃锁，使自己处于等等状态（将当前线程暂停），让其他线程执行。
2. notify():唤醒当前： 当生产者/消费者向缓冲区放入/取出一个产品时，将等待中的线程唤醒（恢复执行），同时放弃锁，使自己处于等待状态。
3. notifyAll()唤醒所有:
      以上3个方法 主要就是用在同步锁中
       
       sleep()；休眠-----------Thread（基类）

* sleep():休眠一段时间  时间到了以后 会自己唤醒
                     * wait(): 等待 不能自己唤醒 必须要notify或者notifyAll来帮助唤醒

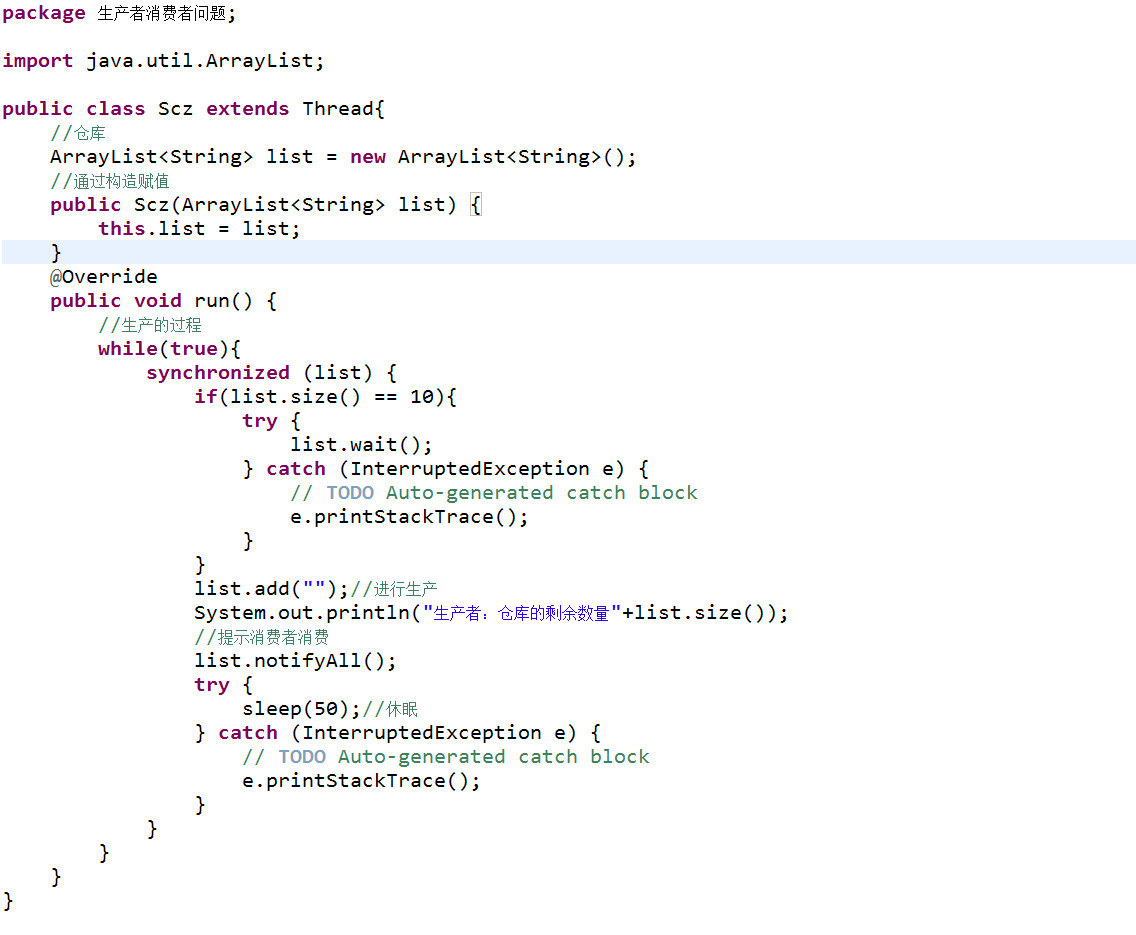
3.生产者

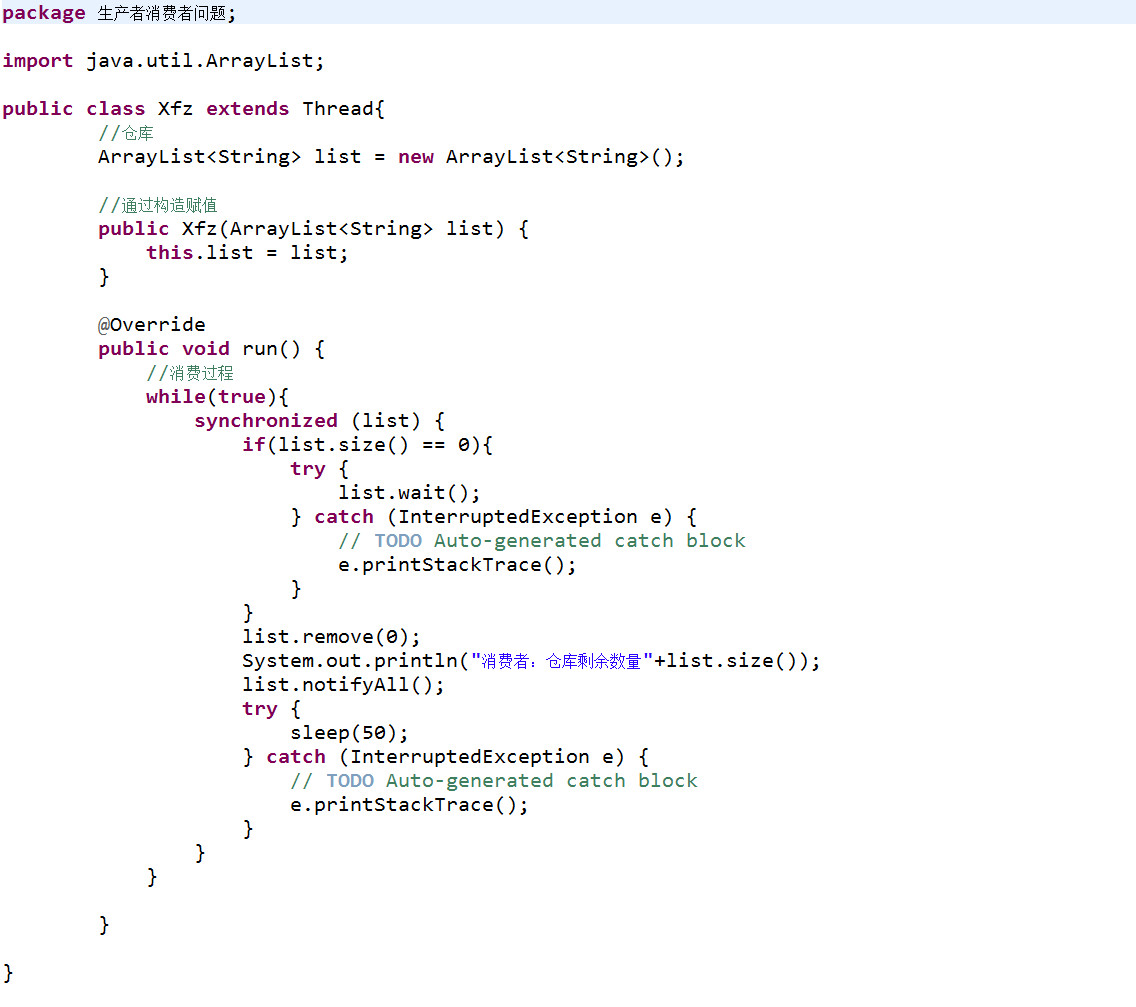
4.消费者

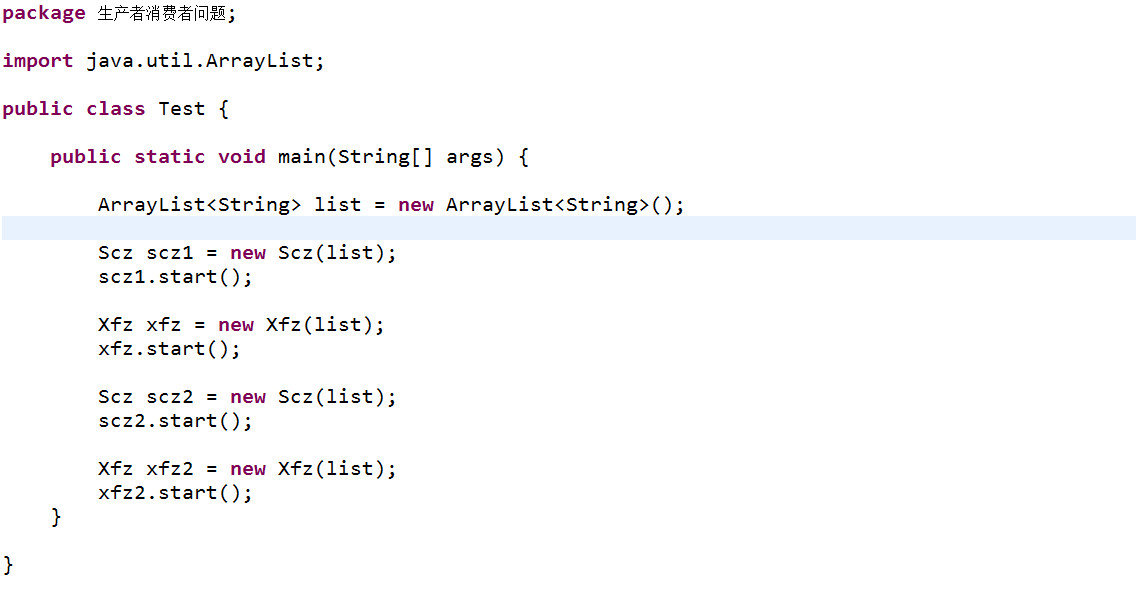
5.生产者与消费者测试类