洛谷 P3711 仓鼠的数学题【伯努利数+多项式科技】

有个东西叫伯努利数……一开始直接·用第一类斯特林推到自闭

式子来源：https://www.luogu.org/blog/ShadowassIIXVIIIIV/solution-p3711

https://blog.csdn.net/q582116859/article/details/79112594 懒得打了

伯努利数：





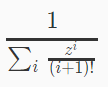
这样就把x放下来了，然后推式子





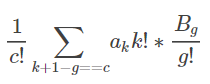
然后枚举x的指数，再reverse一下某个部分，就可以构造出卷积了

#include<iostream>
#include<cstdio>
using namespace std;
const int N=5000005,mod=998244353;
int n,a[N],b[N],c[N],re[N],bt,lm,fac[N],inv[N],t[N],p[N];
int read()
{
    int r=0,f=1;
    char p=getchar();
    while(p>'9'||p<'0')
    {
        if(p=='-')
            f=-1;
        p=getchar();
    }
    while(p>='0'&&p<='9')
    {
        r=r*10+p-48;
        p=getchar();
    }
    return r*f;
}
int ksm(int a,int b)
{
    int r=1;
    while(b)
    {
        if(b&1)
            r=1ll*r*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return r;
}
void dft(int a[],int f,int lm)
{
    for(int i=0;i<lm;i++)
        if(i<re[i])
            swap(a[i],a[re[i]]);
    for(int i=1;i<lm;i<<=1)
    {
        int wi=ksm(3,(mod-1)/(i*2));
        if(f==-1)
            wi=ksm(wi,mod-2);
        for(int k=0;k<lm;k+=(i<<1))
        {
            int w=1,x,y;
            for(int j=0;j<i;j++)
            {
                x=a[j+k],y=1ll*w*a[i+j+k]%mod;
                a[j+k]=(x+y)%mod,a[i+j+k]=(x-y+mod)%mod;
                w=1ll*w*wi%mod;
            }
        }
    }
    if(f==-1)
    {
        int ni=ksm(lm,mod-2);
        for(int i=0;i<lm;i++)
            a[i]=1ll*a[i]*ni%mod;
    }
}
void qiuni(int len)
{
    if(len==1)
        return;
    qiuni(len>>1);
    for(int i=0;i<len;i++)
        t[i]=b[i];
    for(bt=1;(1<<bt)<=2*len;bt++);
    lm=(1<<bt);
    for(int i=0;i<lm;i++)
        re[i]=(re[i>>1]>>1)|((i&1)<<(bt-1));
    dft(t,1,lm);
    dft(p,1,lm);
    for(int i=0;i<lm;i++)
        p[i]=1ll*p[i]*(2-1ll*p[i]*t[i]%mod+mod)%mod;
    dft(p,-1,lm);
    for(int i=0;i<lm;i++)
        t[i]=0;
    for(int i=len;i<lm;i++)
        p[i]=0;
}
int main()
{
    n=read();
    fac[0]=inv[0]=1;
    for(int i=1;i<=2*n;i++)
        fac[i]=1ll*fac[i-1]*i%mod;
    inv[2*n]=ksm(fac[2*n],mod-2);
    for(int i=2*n-1;i>=1;i--)
        inv[i]=1ll*inv[i+1]*(i+1)%mod;
    for(int i=0;i<=n;i++)
        a[i]=1ll*read()*fac[i]%mod;
    printf("%d ",a[0]);
    for(int i=0;i<=n+1;i++)
        b[i]=inv[i+1];
    for(bt=1;(1<<bt)<=n+1;bt++);
    lm=(1<<bt);
    p[0]=1;
    qiuni(lm);
    for(int i=n+1;i<lm;i++)
        p[i]=0;
    p[1]=499122177;
    for(int i=0;i<=n;i++)
        c[n-i+1]=p[i];
    for(bt=1;(1<<bt)<=2*n+3;bt++);
    lm=(1<<bt);
    for(int i=0;i<lm;i++)
        re[i]=(re[i>>1]>>1)|((i&1)<<(bt-1));
    dft(a,1,lm);
    dft(c,1,lm);
    for(int i=0;i<lm;i++)
        a[i]=1ll*a[i]*c[i]%mod;
    dft(a,-1,lm);
    for(int i=1;i<=n+1;i++)
        printf("%lld ",(1ll*inv[i]*a[n+i]%mod+mod)%mod);
    return 0;
}