bzoj3514 Codechef MARCH14 GERALD07加强版 lct预处理+主席树

Codechef MARCH14 GERALD07加强版

Time Limit: 60 Sec  Memory Limit: 256 MB
Submit: 1951  Solved: 746
[Submit][Status][Discuss]

Description

N个点M条边的无向图，询问保留图中编号在[l,r]的边的时候图中的联通块个数。

Input

第一行四个整数N、M、K、type，代表点数、边数、询问数以及询问是否加密。
接下来M行，代表图中的每条边。
接下来K行，每行两个整数L、R代表一组询问。对于type=0的测试点，读入的L和R即为询问的L、R；对于type=1的测试点，每组询问的L、R应为L xor lastans和R xor lastans。

Output

K行每行一个整数代表该组询问的联通块个数。

Sample Input

3 5 4 0
1 3
1 2
2 1
3 2
2 2
2 3
1 5
5 5
1 2

Sample Output

2
1
3
1

HINT

对于100%的数据，1≤N、M、K≤200,000。

2016.2.26提高时限至60s

Source

By zhonghaoxi

题解：

　　首先把边依次加到图中，若当前这条边与图中的边形成了环，那么把这个环中最早加进来的边弹出去
　　并将每条边把哪条边弹了出去记录下来：ntr[i] = j，特别地，要是没有弹出边，ntr[i] = 0;
　　这个显然是可以用LCT来弄的对吧。
　　然后对于每个询问，我们的答案就是对l~r中ntr小于l的边求和，并用n减去这个值
　　正确性可以YY一下：
　　如果一条边的ntr >= l,那么显然他可以与从l ~ r中的边形成环，那么它对答案没有贡献
　　反之如果一条边的ntr < l那么它与从l ~ r中的边是不能形成环的，那么他对答案的贡献为-1
　　对于查询从l ~ r中有多少边的ntr小于l。

　　函数式线段树询问即可

　　

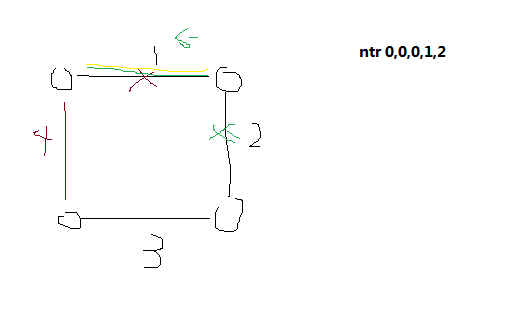
　　比如这个图，如果询问2-5那么，对于5这条边来说，是没意义的，因为5只能将

　　2这条边的效果去掉，因为2最早，所以不能算，

　　因此ans=4-3=1而不是4-4=0

　　

　　函数式线段树记录什么呢，就是rt[i]表示i为右端点，

　　然后左端点的话就是维护前缀和的形式即可。

 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #include<cstdio>

 #define inf 1000000000
 #define ll long long
 #define N 400005
 #define M 200005
 #define NUM 4000007
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }

 int n,m,q,ans,tot,sz,flag;
 int s[N],st[M],root[M];
 int c[N][],fa[N],val[N],mn[N],sum[NUM],ls[NUM],rs[NUM],rev[N];
 struct Node
 {
     int u,v;
 }e[M];

 inline bool isroot(int x){return c[fa[x]][]!=x&&c[fa[x]][]!=x;}
 void update(int p)
 {
     int l=c[p][],r=c[p][];mn[p]=p;
     if(val[mn[l]]<val[mn[p]])mn[p]=mn[l];
     if(val[mn[r]]<val[mn[p]])mn[p]=mn[r];
 }
 void pushdown(int x)
 {
     int l=c[x][],r=c[x][];
     if(rev[x])
     {
         rev[x]^=;rev[l]^=;rev[r]^=;
         swap(c[x][],c[x][]);
     }
 }
 void rotate(int x)
 {
     int y=fa[x],z=fa[y],l,r;
     if(c[y][]==x)l=;else l=;r=l^;
     if(!isroot(y))
     {
         if(c[z][]==y)c[z][]=x;else c[z][]=x;
     }
     fa[y]=x,fa[x]=z,fa[c[x][r]]=y;
     c[y][l]=c[x][r],c[x][r]=y;
     update(y),update(x);
 }
 void splay(int x)
 {
     int top=;s[++top]=x;
     for(int i=x;!isroot(i);i=fa[i])s[++top]=fa[i];
     for(int i=top;i;i--)pushdown(s[i]);
     while(!isroot(x))
     {
         int y=fa[x],z=fa[y];
         if(!isroot(y))
         {
             if(c[y][]==x^c[z][]==y)rotate(x);
             else rotate(y);
         }
         rotate(x);
     }
     update(x);
 }
 void access(int x)
 {
     for(int t=;x!=;t=x,x=fa[x])
         splay(x),c[x][]=t,update(x);
 }
 void makeroot(int x)
 {
     access(x);
     splay(x);
     rev[x]^=;
 }
 void link(int x,int y)
 {
     makeroot(x);
     fa[x]=y;
 }
 void cut(int x,int y)
 {
     makeroot(x),access(y),splay(y);
     c[y][]=fa[x]=;
 }
 int find(int x)
 {
     access(x),splay(x);
     while(c[x][])
         x=c[x][];
     return x;
 }
 int query(int x,int y)
 {
     makeroot(x);
     access(y);
     splay(y);
     return mn[y];
 }
 void ins(int l,int r,int x,int &y,int val)
 {
     y=++sz,sum[y]=sum[x]+;
     if(l==r)return;
     ls[y]=ls[x];rs[y]=rs[x];
     int mid=(l+r)>>;
     if(val<=mid)ins(l,mid,ls[x],ls[y],val);
     else ins(mid+,r,rs[x],rs[y],val);
 }
 int query(int l,int r,int x,int y,int val)
 {
     if(r==val)return sum[y]-sum[x];
     int mid=(l+r)>>;
     if(val<=mid)return query(l,mid,ls[x],ls[y],val);
     else return sum[ls[y]]-sum[ls[x]]+query(mid+,r,rs[x],rs[y],val);
 }
 void init()
 {
     tot=n;
     for(int i=;i<=m;i++)
     {
         int u=e[i].u,v=e[i].v;
         if(u==v){st[i]=i;continue;}
         if(find(u)==find(v))
         {
             int t=query(u,v),x=val[t];
             st[i]=x;
             cut(e[x].u,t);cut(e[x].v,t);
         }
         tot++,mn[tot]=tot,val[tot]=i;
         link(u,tot),link(v,tot);
     }
     for(int i=;i<=m;i++)
         ins(,m,root[i-],root[i],st[i]);
 }
 int main()
 {
     n=read(),m=read(),q=read(),flag=read();
     val[]=inf;
     for(int i=;i<=n;i++) mn[i]=i,val[i]=inf;
     for(int i=;i<=m;i++) e[i].u=read(),e[i].v=read();

     init();

     for(int i=;i<=q;i++)
     {
         int l=read(),r=read();
         if(flag)l^=ans,r^=ans;
         ans=n-query(,m,root[l-],root[r],l-);
         printf("%d\n",ans);
     }
 }